Find x and y, if:
![]()

Comparing the corresponding elements, we get,
6x - 10 = 8
![]() 6x = 18
6x = 18
![]() x = 3
x = 3
-2x + 14 = 4y
![]() 4y = -6+ 14 = 8
4y = -6+ 14 = 8
![]() y = 2
y = 2
Find x and y, if:
![]()

Comparing the corresponding elements, we get,
3x + 18 = 15
![]() 3x = -3
3x = -3
![]() x = -1
x = -1
12x + 77 = 10y
![]() 10y = -12 + 77 = 65
10y = -12 + 77 = 65
![]() y = 6.5
y = 6.5
If ![]() ; find x and y, if:
; find x and y, if:
(i) x, y Î W (whole numbers)
(ii) x, y Î Z (integers)

(i) x, y Î W (whole numbers)
It can be observed that the above two equations are satisfied when x = 3 and y = 4.
(ii) x, y Î Z (integers)
It can be observed that the above two equations are satisfied when x = ![]() 3 and y =
3 and y = ![]() 4.
4.
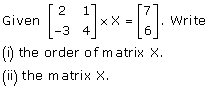
(i)
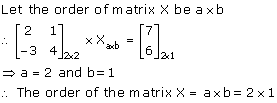
(ii)
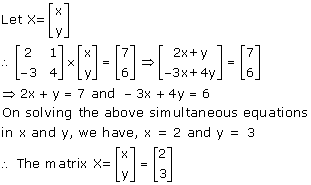
Evaluate:
![]()

If![]() and 3A x M = 2B; find matrix M.
and 3A x M = 2B; find matrix M.
Let the order of matrix M be a x b.
3A x M = 2B
![]()
Clearly, the order of matrix M is 2 x 1.
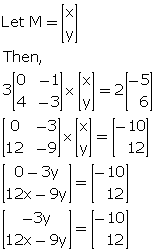
Comparing the corresponding elements, we get,
-3y = -10
![]() y =
y = ![]()
12x - 9y = 12

If ![]() , find the values of a, b and c.
, find the values of a, b and c.
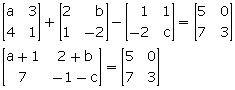
Comparing the corresponding elements, we get,
a + 1 = 5 ![]() a = 4
a = 4
2 + b = 0 ![]() b = -2
b = -2
-1 - c = 3 ![]() c = -4
c = -4
If A = ![]() ; find:
; find:
(i) A (BA)
(ii) (AB). B
![]()
(i)

(ii)
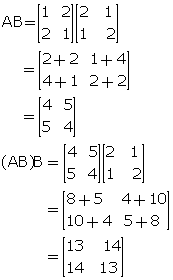
Find x and y, if: ![]()
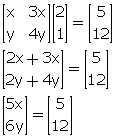
Comparing the corresponding elements, we get,
5x = 5![]() x = 1
x = 1
6y = 12![]() y = 2
y = 2
If matrix X =![]() and 2X - 3Y =
and 2X - 3Y =![]() ; find the matrix 'X' and 'Y'.
; find the matrix 'X' and 'Y'.
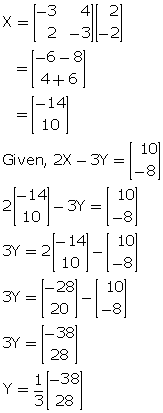
Given ![]() ; find the matrix X such that:
; find the matrix X such that:
A + X = 2B + C
Given, A + X = 2B + C

Find the value of x, given that A2 = B,
![]()
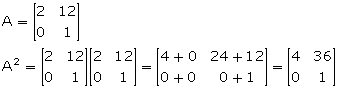
Given, A2 = B
![]()
Comparing the corresponding elements, we get,
x = 36
If ![]() , and I is identity matrix of the same order and At is the transpose of matrix A, find At .B + BI
, and I is identity matrix of the same order and At is the transpose of matrix A, find At .B + BI

Let![]() . Find A2 - A + BC.
. Find A2 - A + BC.
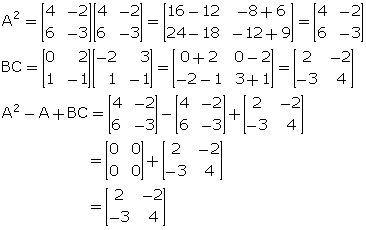
Let A =![]() . Find A2 + AB + B2.
. Find A2 + AB + B2.
A = ![]()
A2 = A ![]() A =
A = ![]()
= ![]()
AB = A ![]() B =
B = ![]()
=![]()
= ![]()
B2 = B x B = ![]()
= ![]()
= ![]()
![]() A2 + AB + B2 =
A2 + AB + B2 = ![]()
= ![]()
If ![]() and 3A - 2C = 6B, find the values of a, b and c.
and 3A - 2C = 6B, find the values of a, b and c.
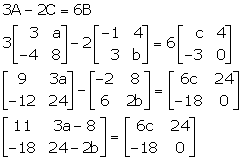
Comparing the corresponding elements, we get,
3a - 8 = 24 ![]() 3a = 32
3a = 32 ![]() a =
a = ![]()
24 - 2b = 0 ![]() 2b = 24
2b = 24 ![]() b = 12
b = 12
11 = 6c ![]() c =
c = ![]()
Given A =![]() .
.
Find the values of p and q.
A = ![]()
BA = ![]()
C2 = ![]()
BA = C2 ![]()
![]() =
=![]()
By comparing,
-2q = -8 ![]() q = 4
q = 4
And p = 8
Given A =![]() . Find AB + 2C - 4D.
. Find AB + 2C - 4D.
AB = ![]()
![]()
![]()
Evaluate:
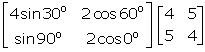
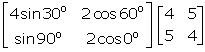
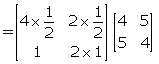
= ![]()
= ![]()
![]()
![]()
A2 = 9A + MI
⇒ A2 - 9A = mI ….(1)
Now, A2 = AA
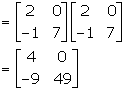
Substituting A2 in (1), we have
A2 - 9A = mI
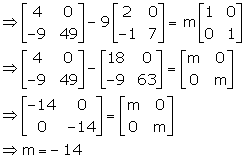
![]()
(i) Write the order of matrix X.
(ii) Find the matrix 'X'
![]()
(i) Let the order of matrix X = m × n
Order of matrix A = 2 × 2
Order of matrix B = 2 × 1
Now, AX = B
∴ m = 2 and n = 1
Thus, order of matrix X = m × n = 2 × 1
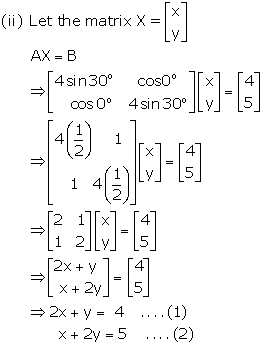
Multiplying (1) by 2, we get
4x + 2y = 8 ….(3)
Subtracting (2) from (3), we get
3x = 3
⇒ x = 1
Substituting the value of x in (1), we get
2(1) + y = 4
⇒ 2 + y = 4
⇒ y = 2
![]()
![]() Find the matrix C where C is a 2 by 2 matrix.
Find the matrix C where C is a 2 by 2 matrix.
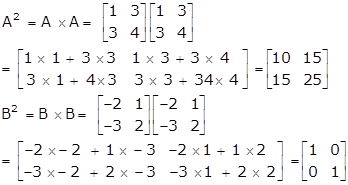
Given: A2 - 5B2 = 5C
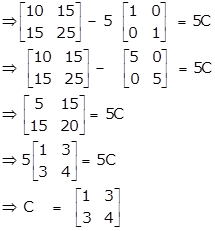
Given matrix ![]() . Find the matrix X if, X = B2 - 4B. Hence, solve for a and b given
. Find the matrix X if, X = B2 - 4B. Hence, solve for a and b given ![]() .
.
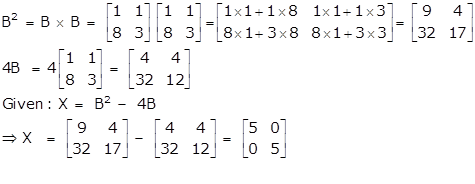
To find: a and b
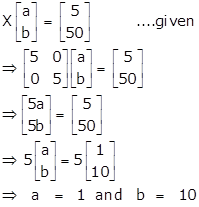
No comments:
Post a Comment