Chapter 15 - Similarity (With Applications to Maps and Models) Exercise Ex. 15(B)

Question 1(i)

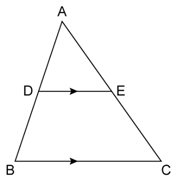
In the following figure, point D divides AB in the ratio 3 : 5. Find :

 

 

Solution 1(i)

Now, DE is parallel to BC.

Then, by Basic proportionality theorem, we have

 

Question 1(ii)

In the following figure, point D divides AB in the ratio 3 : 5. Find :

 

 

Solution 1(ii)

 

Question 1(iii)

In the following figure, point D divides AB in the ratio 3 : 5. Find :

 

 

Solution 1(iii)

 

Question 1(iv)

In the following figure, point D divides AB in the ratio 3 : 5. Find :

DE = 2.4 cm, find the length of BC.

 

Solution 1(iv)

 

Question 1(v)

In the following figure, point D divides AB in the ratio 3 : 5. Find :

BC = 4.8 cm, find the length of DE.

 

Solution 1(v)

 

Question 2(i)

In the given figure, PQ ‖ AB; CQ = 4.8 cm QB = 3.6 cm and AB = 6.3 cm. Find :

 

 

Solution 2(i)

 

Question 2(ii)

In the given figure, PQ ‖ AB; CQ = 4.8 cm QB = 3.6 cm and AB = 6.3 cm. Find :

PQ

 

Solution 2(ii)

 

Question 2(iii)

In the given figure, PQ ‖ AB; CQ = 4.8 cm QB = 3.6 cm and AB = 6.3 cm. Find :

If AP = x, then the value of AC in terms of x.  

Solution 2(iii)

 

Question 3

A line PQ is drawn parallel to the side BC of Δ ABC which cuts side AB at P and side AC at Q. If AB = 9.0 cm, CA = 6.0 cm and AQ = 4.2 cm, find the length of AP.

Solution 3

 

 

 

 

Question 4(i)

In Δ ABC, D and E are the points on sides AB and AC respectively.

Find whether DE ‖ BC, if

AB = 9cm, AD = 4cm, AE = 6cm and EC = 7.5cm. 

Solution 4(i)

 

 

 

 

 

Question 4(ii)

In Δ ABC, D and E are the points on sides AB and AC respectively.

Find whether DE ‖ BC, if AB = 6.3 cm, EC = 11.0 cm, AD =0.8 cm and EA = 1.6 cm.

Solution 4(ii)

 

 

 

 

 

 

Question 5

In the given figure, Δ ABC ~ Δ ADE. If AE: EC = 4 : 7 and DE = 6.6 cm, find BC. If 'x' be the length of the perpendicular from

 

 

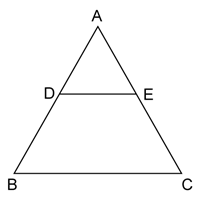
A to DE, find the length of perpendicular from A to BC in terms of 'x'.

Solution 5

 

 

 

 

Question 6

A line segment DE is drawn parallel to base BC of Δ ABC which cuts AB at point D and AC at point E. If AB = 5BD and EC = 3.2 cm, find the length of AE.

Solution 6

 

 

 

 

 

 

Question 7

In the figure, given below, AB, CD and EF are parallel lines. Given AB = 7.5 cm, DC = y cm, EF = 4.5 cm, BC = x cm and CE = 3. cm, calculate the values of x and y.

 

 

 

Solution 7

 

Question 8

In the figure, given below, PQR is a right-angle triangle right angled at Q. XY is parallel to QR, PQ = 6 cm, PY = 4 cm and PX : XQ = 1 : 2. Calculate the lengths of PR and QR.

 

 

Solution 8

 

Question 9

In the following figure, M is mid-point of BC of a parallelogram ABCD. DM intersects the diagonal AC at P and AB produced at E.

Prove that : PE = 2 PD 

 

 

Solution 9

 

Question 10

The given figure shows a parallelogram ABCD. E is a point in AD and CE produced meets BA produced at point F. If AE = 4 cm, AF = 8 cm and AB = 12 cm, find the perimeter of the parallelogram ABCD.

 

Solution 10