Chapter 18 - Tangents and Intersecting Chords Exercise Ex. 18(A)

Question 1

The radius of a circle is 8 cm. Calculate the length of a tangent drawn to this circle from a point at a distance of 10 cm from its centre?

Solution 1

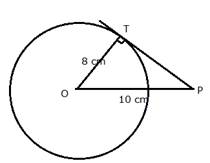
OP = 10 cm; radius OT = 8 cm

Length of tangent = 6 cm.

Question 2

In the given figure, O is the centre of the circle and AB is a tangent to the circle at B. If AB = 15 cm and AC = 7.5 cm, calculate the radius of the circle.

Solution 2

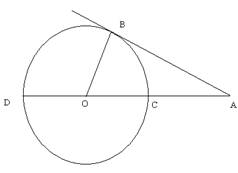
AB = 15 cm, AC = 7.5 cm

Let 'r' be the radius of the circle.

OC = OB = r

AO = AC + OC = 7.5 + r

In ∆AOB,

AO² = AB² + OB²

 

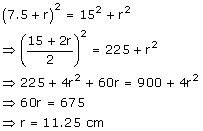
Therefore,  r = 11.25 cm

Question 3

Two circles touch each other externally at point P. Q is a point on the common tangent through P. Prove that the tangents QA and QB are equal.

Solution 3

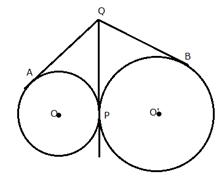
From Q, QA and QP are two tangents to the circle with centre O

Therefore, QA = QP .....(i)

Similarly, from Q, QB and QP are two tangents to the circle with centre O'

Therefore, QB = QP ......(ii)

From (i) and (ii)

QA = QB

Therefore, tangents QA and QB are equal.

Question 4

Two circles touch each other internally. Show that the tangents drawn to the two circles from any point on the common tangent are equal in length.

Solution 4

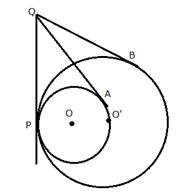
From Q, QA and QP are two tangents to the circle with centre O

Therefore, QA = QP .......(i)

Similarly, from Q, QB and QP are two tangents to the circle with centre O'

Therefore, QB = QP .......(ii)

From (i) and (ii)

QA = QB

Therefore, tangents QA and QB are equal.

Question 5

Two circles of radii 5 cm and 3 cm are concentric. Calculate the length of a chord of the outer circle which touches the inner.

Solution 5

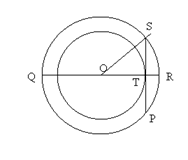
OS = 5 cm

OT = 3 cm

In Rt. Triangle OST

By Pythagoras Theorem,

Since OT is perpendicular to SP and OT bisects chord SP

So, SP = 8 cm

Question 6

Three circles touch each other externally. A triangle is formed when the centers of these circles are joined together. Find the radii of the circles, if the sides of the triangle formed are 6 cm, 8 cm and 9 cm.

Solution 6

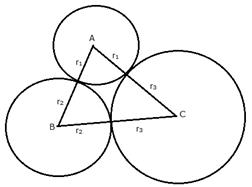
AB = 6 cm, AC = 8 cm and BC = 9 cm

Let radii of the circles having centers A, B and C be r₁, r₂ and r₃ respectively.

r₁ + r₃ = 8

r₃ + r₂ = 9

r₂ + r₁ = 6

Adding

r₁ + r₃ + r₃ + r₂ + r₂ + r₁ = 8+9+6

2(r₁ + r₂ + r₃) = 23

r₁ + r₂ + r₃ = 11.5 cm

r₁ + 9 = 11.5 (Since r₂ + r₃ = 9)

r₁ = 2.5 cm

r₂ + 6 = 11.5 (Since r₁ + r₃ = 6)

r₂ = 5.5 cm

r₃ + 8 = 11.5 (Since r₂ + r₁ = 8)

r₃ = 3.5 cm

Hence, r₁ = 2.5 cm, r₂ = 5.5 cm and r₃ = 3.5 cm

Question 7

 

If the sides of a quadrilateral ABCD touch a circle, prove that AB + CD = BC + AD.

Solution 7

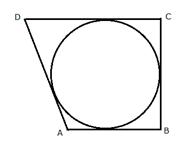
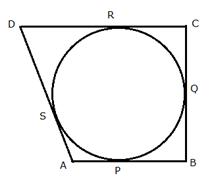
Let the circle touch the sides AB, BC, CD and DA of quadrilateral ABCD at P, Q, R and S respectively.

Since AP and AS are tangents to the circle from external point A

AP = AS .......(i)

Similarly, we can prove that:

BP = BQ .......(ii)

CR = CQ .......(iii)

DR = DS ........(iv)

Adding,

AP + BP + CR + DR = AS + DS + BQ + CQ

AB + CD = AD + BC

Hence, AB + CD = AD + BC

Question 8

If the sides of a parallelogram touch a circle, prove that the parallelogram is a rhombus.

Solution 8

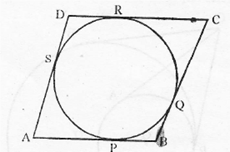
From A, AP and AS are tangents to the circle.

Therefore, AP = AS.......(i)

Similarly, we can prove that:

BP = BQ .........(ii)

CR = CQ .........(iii)

DR = DS .........(iv)

Adding,

AP + BP + CR + DR = AS + DS + BQ + CQ

AB + CD = AD + BC

Hence, AB + CD = AD + BC

But AB = CD and BC = AD.......(v) Opposite sides of a ||gm

Therefore, AB + AB = BC + BC

2AB = 2 BC

AB = BC ........(vi)

From (v) and (vi)

AB = BC = CD = DA

Hence, ABCD is a rhombus.

Question 9

From the given figure prove that:

AP + BQ + CR = BP + CQ + AR.

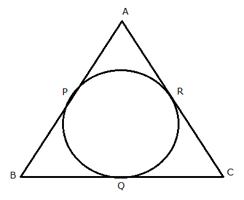
Also, show that AP + BQ + CR = x perimeter of triangle ABC.

Solution 9

Since from B, BQ and BP are the tangents to the circle

Therefore, BQ = BP ………..(i)

Similarly, we can prove that

AP = AR …………..(ii)

and CR = CQ ………(iii)

Adding,

AP + BQ + CR = BP + CQ + AR ………(iv)

Adding AP + BQ + CR to both sides

2(AP + BQ + CR) = AP + PQ + CQ + QB + AR + CR

2(AP + BQ + CR) = AB + BC + CA

Therefore, AP + BQ + CR =  x (AB + BC + CA)

AP + BQ + CR =  x perimeter of triangle ABC

Question 10

In the figure, if AB = AC then prove that BQ = CQ.

Solution 10

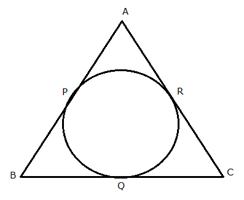
Since, from A, AP and AR are the tangents to the circle

Therefore, AP = AR

Similarly, we can prove that

BP = BQ and CR = CQ

Adding,

AP + BP + CQ = AR + BQ + CR

(AP + BP) + CQ = (AR + CR) + BQ

AB + CQ = AC + BQ

But AB = AC

Therefore, CQ = BQ or BQ = CQ

Question 11

Radii of two circles are 6.3 cm and 3.6 cm. State the distance between their centers if -

i) they touch each other externally.

ii) they touch each other internally.

Solution 11

Radius of bigger circle = 6.3 cm

and of smaller circle = 3.6 cm

i)

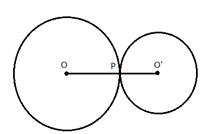
Two circles are touching each other at P externally. O and O’ are the centers of the circles. Join OP and O’P

OP = 6.3 cm, O’P = 3.6 cm

Adding,

OP + O’P = 6.3 + 3.6 = 9.9 cm

ii)

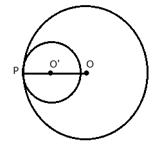
Two circles are touching each other at P internally. O and O’ are the centers of the circles. Join OP and O’P

OP = 6.3 cm, O’P = 3.6 cm

OO’ = OP - O’P = 6.3 - 3.6 = 2.7 cm

Question 12

From a point P outside the circle, with centre O, tangents PA and PB are drawn. Prove that:

i) 

ii) OP is the perpendicular bisector of chord AB.

Solution 12

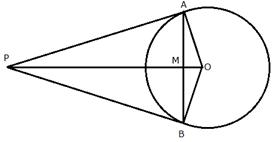
i) In 

AP = BP (Tangents from P to the circle)

OP = OP (Common)

OA = OB (Radii of the same circle)

ii) In 

OA = OB (Radii of the same circle)

 (Proved )

OM = OM (Common)

Hence, OM or OP is the perpendicular bisector of chord AB.

Question 13

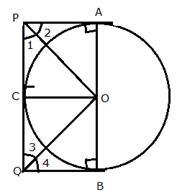
In the given figure, two circles touch each other externally at point P. AB is the direct common tangent of these circles. Prove that:

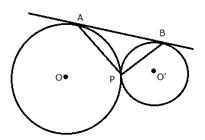
i) tangent at point P bisects AB.

ii) Angle APB = 90°

Solution 13

Draw TPT' as common tangent to the circles.

i) TA and TP are the tangents to the circle with centre O.

Therefore, TA = TP ………(i)

Similarly, TP = TB ………..(ii)

From (i) and (ii)

TA = TB

Therefore, TPT' is the bisector of AB.

ii) Now in 

Similarly in  

Adding,

Question 14

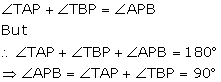
Tangents AP and AQ are drawn to a circle, with centre O, from an exterior point A. Prove that:

Solution 14

In quadrilateral OPAQ,

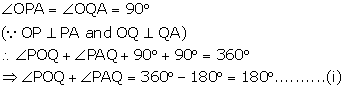
In triangle OPQ,

OP = OQ (Radii of the same circle)

From (i) and (ii)

Question 15

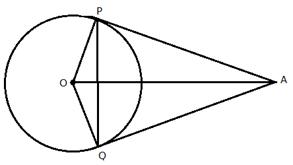
Two parallel tangents of a circle meet a third tangent at point P and Q. Prove that PQ subtends a right angle at the centre.

Solution 15

Join OP, OQ, OA, OB and OC.

In 

OA = OC (Radii of the same circle)

OP = OP (Common)

PA = PC (Tangents from P)

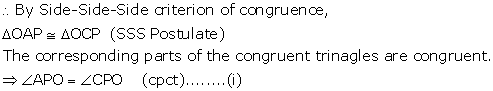
Similarly, we can prove that

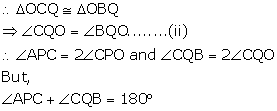
(Sum of interior angles of a transversal)

Now in 

Question 16

ABC is a right angled triangle with AB = 12 cm and AC = 13 cm. A circle, with centre O, has been inscribed inside the triangle.

Calculate the value of x, the radius of the inscribed circle.

Solution 16

In 

LBNO is a square.

LB = BN = OL = OM = ON = x

Since ABC is a right triangle

Question 17

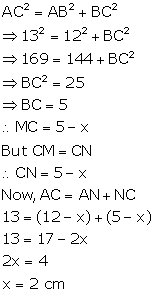
In a triangle ABC, the incircle (centre O) touches BC, CA and AB at points P, Q and R respectively. Calculate:

i) 

ii) 

given that 

Solution 17

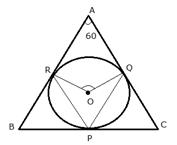
The incircle touches the sides of the triangle ABC and

i) In quadrilateral AROQ,

ii) Now arc RQ subtends  at the centre and at the remaining part of the circle.

Question 18

In the following figure, PQ and PR are tangents to the circle, with centre O. If , calculate:

i) 

ii) 

iii)

Solution 18

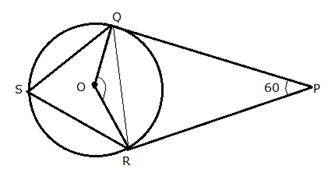
Join QR.

i) In quadrilateral ORPQ,

ii) In 

OQ = QR (Radii of the same circle)

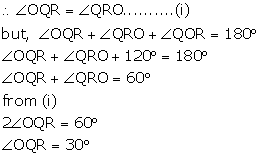
iii) Now arc RQ subtends  at the centre and at the remaining part of the circle.

Question 19

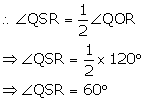
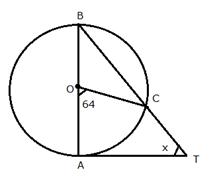
In the given figure, AB is a diameter of the circle, with centre O, and AT is a tangent. Calculate the numerical value of x.

Solution 19

In 

OB = OC (Radii of the same circle)

Now in 

Question 20

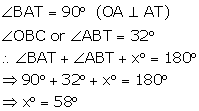
In quadrilateral ABCD, angle D = 90°, BC = 38 cm and DC = 25 cm. A circle is inscribed in this quadrilateral which touches AB at point Q such that QB = 27 cm. Find the radius of the circle.

Solution 20

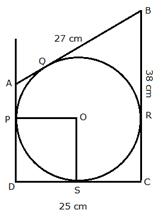
BQ and BR are the tangents from B to the circle.

Therefore, BR =BQ = 27 cm.

Also RC = (38 -; 27) = 11cm

Since CR and CS are the tangents from C to the circle

Therefore, CS = CR = 11 cm

So, DS = (25 - 11) = 14 cm

Now DS and DP are the tangents to the circle

Therefore, DS = DP

Now,  (given)

and 

therefore, radius = DS = 14 cm

Question 21

In the given figure, PT touches the circle with centre O at point R. Diameter SQ is produced to meet the tangent TR at P.

Given  and 

Prove that -;

i) 

ii) write an expression connecting x and y

Solution 21

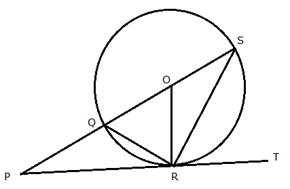
(angles in alternate segment)

But OS = OR (Radii of the same circle)

But in 

From (i) and (ii)

Question 22

PT is a tangent to the circle at T. If ; calculate:

i) 

ii) 

iii) 

Solution 22

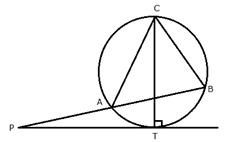
Join AT and BT.

i) TC is the diameter of the circle

 (Angle in a semi-circle)

ii) 

 (Angles in the same segment of the

circle)

(Angles in the same segment of the circle)

iii)  (Angles in the same segment)

Now in 

Question 23

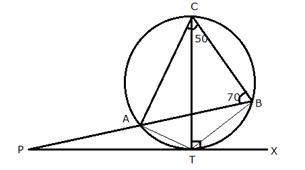
In the given figure, O is the centre of the circumcircle ABC. Tangents at A and C intersect at P. Given angle AOB = 140° and angle APC = 80°; find the angle BAC.

Solution 23

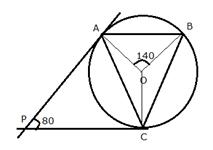
Join OC.

Therefore, PA and PA are the tangents

In quadrilateral APCO,

Now, arc BC subtends  at the centre and  at the remaining part of the circle

Question 24

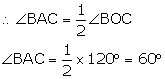
In the given figure, PQ is a tangent to the circle at A. AB and AD are bisectors of ∠CAQ and ∠PAC. If ∠BAQ = 30°, prove that : BD is diameter of the circle.

 

 

Solution 24

∠CAB = ∠BAQ = 30°……(AB is angle bisector of ∠CAQ) 

∠CAQ = 2∠BAQ = 60°……(AB is angle bisector of ∠CAQ)

∠CAQ + ∠PAC = 180°……(angles in linear pair)

∴∠PAC = 120°

∠PAC = 2∠CAD……(AD is angle bisector of ∠PAC) 

∠CAD = 60° 

Now,

∠CAD + ∠CAB = 60 + 30 = 90° 

∠DAB = 90° 

Thus, BD subtends 90° on the circle

So, BD is the diameter of circle