(i) 5a + 7b : 5a - 7b = 5c + 7d : 5c - 7d.
(ii) (9a + 13b) (9c - 13d) = (9c + 13d) (9a - 13b).
(iii) xa + yb : xc + yd = b : d.

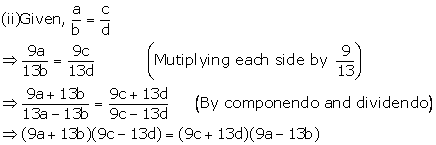

If a : b = c : d, prove that:
(6a + 7b) (3c - 4d) = (6c + 7d) (3a - 4b).

Given, ![]() , prove that:
, prove that:
![]()

If ![]() ; then prove that:
; then prove that:
x: y = u: v.

If (7a + 8b) (7c - 8d) = (7a - 8b) (7c + 8d), prove that a: b = c: d.
Given, ![]()
Applying componendo and dividendo,
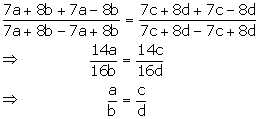
Hence, a: b = c: d.
(i) If x = ![]() , find the value of:
, find the value of:
![]() .
.
(ii) If a = ![]() , find the value of:
, find the value of:
![]()
(i) x = ![]()

(ii) ![]()
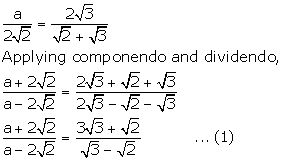

If (a + b + c + d) (a - b - c + d) = (a + b - c - d) (a - b + c - d), prove that a: b = c: d.

If ![]() , show that 2ad = 3bc.
, show that 2ad = 3bc.

If ![]() ; prove that:
; prove that: ![]() .
.
Given, ![]()
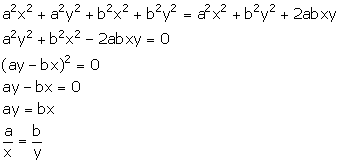
If a, b and c are in continued proportion, prove that:
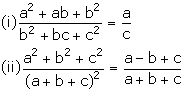
Given, a, b and c are in continued proportion.
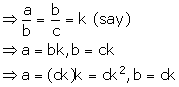
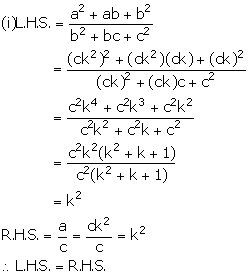
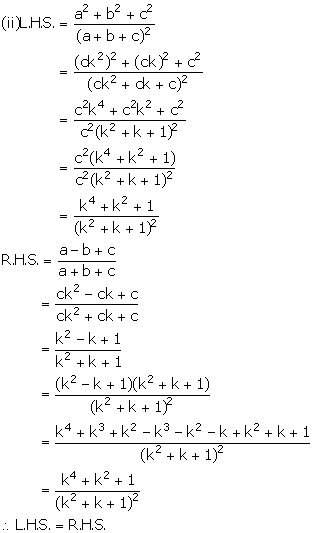
Using properties of proportion, solve for x:
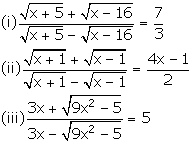



If ![]() , prove that: 3bx2 - 2ax + 3b = 0.
, prove that: 3bx2 - 2ax + 3b = 0.
Since, ![]()
Applying componendo and dividendo, we get,
![]()
![]()
Squaring both sides,
![]()
Again applying componendo and dividendo,
![]()
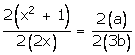
![]()
3bx2 + 3b = 2ax
3bx2 - 2ax + 3b = 0.
If ![]() , express n in terms of x and m.
, express n in terms of x and m.
![]()
Applying componendo and dividendo,
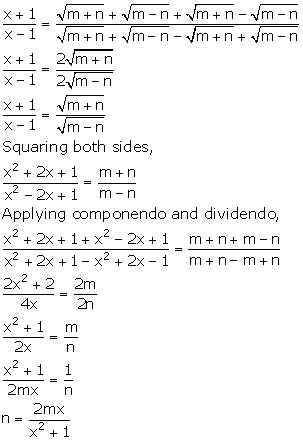
If ![]() , show that:
, show that:
nx = my.
![]()
Applying componendo and dividendo,

No comments:
Post a Comment