Calculate the co-ordinates of the point P which divides the line segment joining:
(i) A (1, 3) and B (5, 9) in the ratio 1: 2.
(ii) A (-4, 6) and B (3, -5) in the ratio 3: 2.
(i) Let the co-ordinates of the point P be (x, y).
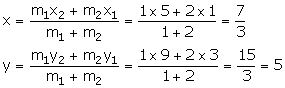
Thus, the co-ordinates of point P are![]() .
.
(ii) Let the co-ordinates of the point P be (x, y).
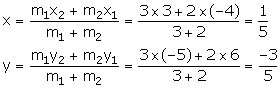
Thus, the co-ordinates of point P are![]() .
.
In what ratio is the line joining (2, -3) and (5, 6) divided by the x-axis.
Let the line joining points A (2, -3) and B (5, 6) be divided by point P (x, 0) in the ratio k: 1.
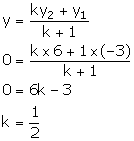
Thus, the required ratio is 1: 2.
In what ratio is the line joining (2, -4) and (-3, 6) divided by the y-axis.
Let the line joining points A (2, -4) and B (-3, 6) be divided by point P (0, y) in the ratio k: 1.
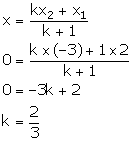
Thus, the required ratio is 2: 3.
In what ratio does the point (1, a) divided the join of (-1, 4) and (4, -1)? Also, find the value of a.
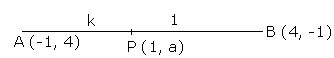
Let the point P (1, a) divides the line segment AB in the ratio k: 1.
Using section formula, we have:

In what ratio does the point (a, 6) divide the join of (-4, 3) and (2, 8)? Also, find the value of a.
Let the point P (a, 6) divides the line segment joining A (-4, 3) and B (2, 8) in the ratio k: 1.
Using section formula, we have:

In what ratio is the join of (4, 3) and (2, -6) divided by the x-axis. Also, find the co-ordinates of the point of intersection.
Let the point P (x, 0) on x-axis divides the line segment joining A (4, 3) and B (2, -6) in the ratio k: 1.
Using section formula, we have:
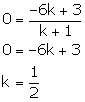
Thus, the required ratio is 1: 2.
Also, we have:
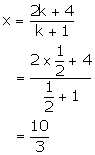
Thus, the required co-ordinates of the point of intersection are ![]() .
.
Find the ratio in which the join of (-4, 7) and (3, 0) is divided by the y-axis. Also, find the coordinates of the point of intersection.
![]()
Let S (0, y) be the point on y-axis which divides the line segment PQ in the ratio k: 1.
Using section formula, we have:
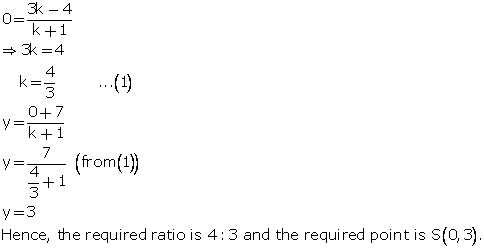
Points A, B, C and D divide the line segment joining the point (5, -10) and the origin in five equal parts. Find the co-ordinates of A, B, C and D.

Point A divides PO in the ratio 1: 4.
Co-ordinates of point A are:
![]()
Point B divides PO in the ratio 2: 3.
Co-ordinates of point B are:
![]()
Point C divides PO in the ratio 3: 2.
Co-ordinates of point C are:
![]()
Point D divides PO in the ratio 4: 1.
Co-ordinates of point D are:
![]()
The line joining the points A (-3, -10) and B (-2, 6) is divided by the point P such that ![]() Find the co-ordinates of P.
Find the co-ordinates of P.
Let the co-ordinates of point P are (x, y).
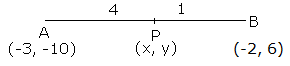
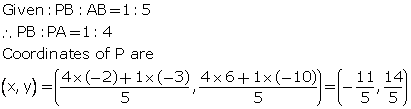
P is a point on the line joining A (4, 3) and B (-2, 6) such that 5AP = 2BP. Find the co-ordinates of P.
5AP = 2BP
![]()
The co-ordinates of the point P are
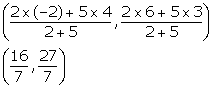
Calculate the ratio in which the line joining the points (-3, -1) and (5, 7) is divided by the line x = 2. Also, find the co-ordinates of the point of intersection.
The co-ordinates of every point on the line x = 2 will be of the type (2, y).
Using section formula, we have:

Thus, the required ratio is 5: 3.
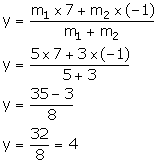
Thus, the required co-ordinates of the point of intersection are (2, 4).
Calculate the ratio in which the line joining A (6, 5) and B (4, -3) is divided by the line y = 2.
The co-ordinates of every point on the line y = 2 will be of the type (x, 2).
Using section formula, we have:
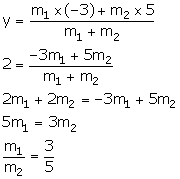
Thus, the required ratio is 3: 5.
The point P (5, -4) divides the line segment AB, as shown in the figure, in the ratio 2: 5. Find the co-ordinates of points A and B.
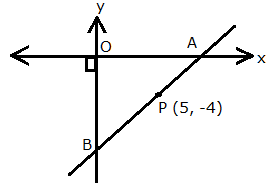
Point A lies on x-axis. So, let the co-ordinates of A be (x, 0).
Point B lies on y-axis. So, let the co-ordinates of B be (0, y).
P divides AB in the ratio 2: 5.
We have:
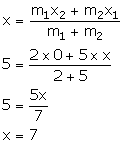
Thus, the co-ordinates of point A are (7, 0).
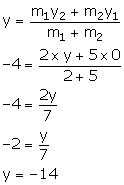
Thus, the co-ordinates of point B are (0, -14).
Find the co-ordinates of the points of trisection of the line joining the points (-3, 0) and (6, 6).
Let P and Q be the point of trisection of the line segment joining the points A (-3, 0) and B (6, 6).
So, AP = PQ = QB
We have AP: PB = 1: 2
Co-ordinates of the point P are

We have AQ: QB = 2: 1
Co-ordinates of the point Q are

Show that the line segment joining the points (-5, 8) and (10, -4) is trisected by the co-ordinate axes.
Let P and Q be the point of trisection of the line segment joining the points A (-5, 8) and B (10, -4).
So, AP = PQ = QB
We have AP: PB = 1: 2
Co-ordinates of the point P are
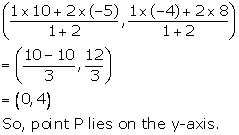
We have AQ: QB = 2: 1
Co-ordinates of the point Q are

So, point Q lies on the x-axis.
Hence, the line segment joining the given points A and B is trisected by the co-ordinate axes.
Show that A (3, -2) is a point of trisection of the line-segment joining the points (2, 1) and (5, -8). Also, find the co-ordinates of the other point of trisection.
Let A and B be the point of trisection of the line segment joining the points P (2, 1) and Q (5, -8).
So, PA = AB = BQ
We have PA: AQ = 1: 2
Co-ordinates of the point A are
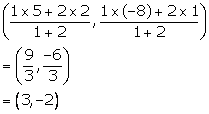
Hence, A (3, -2) is a point of trisection of PQ.
We have PB: BQ = 2: 1
Co-ordinates of the point B are

If A = (-4, 3) and B = (8, -6)
(i) Find the length of AB.
(ii) In what ratio is the line joining A and B, divided by the x-axis?
(i) A (-4,3) and B (8, -6)
AB =![]()

(ii) Let P be the point, which divides AB on the x-axis in the ratio k : 1.
Therefore, y-co-ordinate of P = 0.
![]()
![]() = 0
= 0
![]() -6k + 3 = 0
-6k + 3 = 0
![]() k =
k =![]()
![]() Required ratio is 1: 2.
Required ratio is 1: 2.
The line segment joining the points M (5, 7) and N (-3, 2) is intersected by the y-axis at point L. Write down the abscissa of L. Hence, find the ratio in which L divides MN. Also, find the co-ordinates of L.
Since, point L lies on y-axis, its abscissa is 0.
Let the co-ordinates of point L be (0, y). Let L divides MN in the ratio k: 1.
Using section formula, we have:

Thus, the required ratio is 5: 3.

A (2, 5), B (-1, 2) and C (5, 8) are the co-ordinates of the vertices of the triangle ABC. Points P and Q lie on AB and AC respectively, such that AP: PB = AQ: QC = 1: 2.
(i) Calculate the co-ordinates of P and Q.
(ii) Show that PQ = ![]() BC.
BC.
(i) Co-ordinates of P are

Co-ordinates of Q are

(ii) Using distance formula, we have:
BC = ![]()
PQ = ![]()
Hence, PQ = ![]() BC.
BC.
A (-3, 4), B (3, -1) and C (-2, 4) are the vertices of a triangle ABC. Find the length of line segment AP, where point P lies inside BC, such that BP: PC = 2: 3.
BP: PC = 2: 3
Co-ordinates of P are
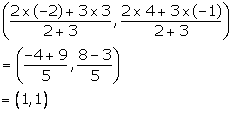
Using distance formula, we have:
![]()
The line segment joining A (2, 3) and B (6, -5) is intercepted by x-axis at the point K. Write down the ordinate of the point K. Hence, find the ratio in which K divides AB. Also, find the co-ordinates of the point K.
Since, point K lies on x-axis, its ordinate is 0.
Let the point K (x, 0) divides AB in the ratio k: 1.
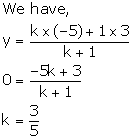
Thus, K divides AB in the ratio 3: 5.
Also, we have:
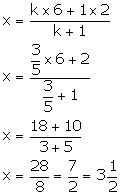
Thus, the co-ordinates of the point K are ![]() .
.
The line segment joining A (4, 7) and B (-6, -2) is intercepted by the y-axis at the point K. Write down the abscissa of the point K. Hence, find the ratio in which K divides AB. Also, find the co-ordinates of the point K.
Since, point K lies on y-axis, its abscissa is 0.
Let the point K (0, y) divides AB in the ratio k: 1.
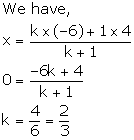
Thus, K divides AB in the ratio 2: 3.
Also, we have:
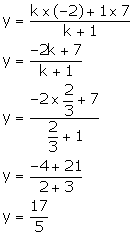
Thus, the co-ordinates of the point K are ![]() .
.
The line joining P (-4, 5) and Q (3, 2) intersects the y-axis at point R. PM and QN are perpendiculars from P and Q on the x-axis. Find:
(i) the ratio PR: RQ.
(ii) the co-ordinates of R.
(iii) the area of the quadrilateral PMNQ.
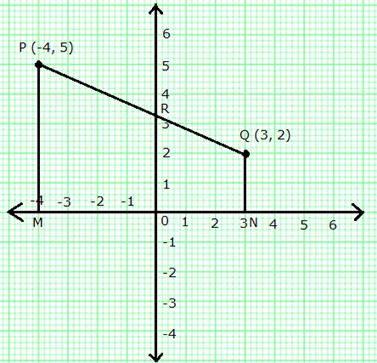
(i) Let point R (0, y) divides PQ in the ratio k: 1.
We have:
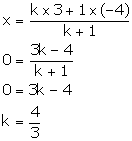
Thus, PR: RQ = 4: 3
(ii) Also, we have:
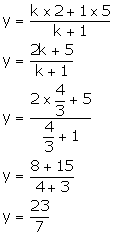
Thus, the co-ordinates of point R are ![]() .
.
(iii) Area of quadrilateral PMNQ
= ![]() (PM + QN)
(PM + QN) ![]() MN
MN
= ![]() (5 + 2)
(5 + 2) ![]() 7
7
= ![]() 7
7 ![]() 7
7
= 24.5 sq units
In the given figure, line APB meets the x-axis at point A and y-axis at point B. P is the point (-4, 2) and AP: PB = 1: 2. Find the co-ordinates of A and B.
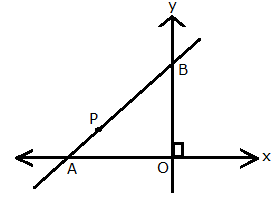
Given, A lies on x-axis and B lies on y-axis.
Let the co-ordinates of A and B be (x, 0) and (0, y) respectively.
Given, P is the point (-4, 2) and AP: PB = 1: 2.
Using section formula, we have:
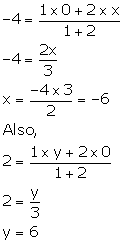
Thus, the co-ordinates of points A and B are (-6, 0) and (0, 6) respectively.
Given a line segment AB joining the points A(-4, 6) and B(8, -3). Find:
(i) the ratio in which AB is divided by the y-axis
(ii) find the coordinates of the point of intersection
(iii) the length of AB
(i)

(ii)
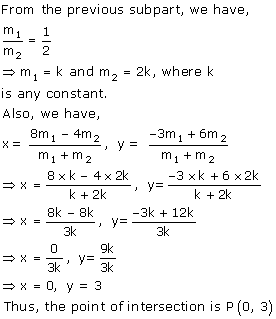
(iii)

If P(-b, 9a - 2) divides the line segment joining the points A(-3, 3a + 1) and B(5, 8a) in the ratio 3: 1, find the values of a and b.
Take (x1 , y1) = (-3, 3a + 1) ; (x2 , y2) = B(5, 8a) and
(x, y) = (-b, 9a - 2)
Here m1 = 3 and m2 =1
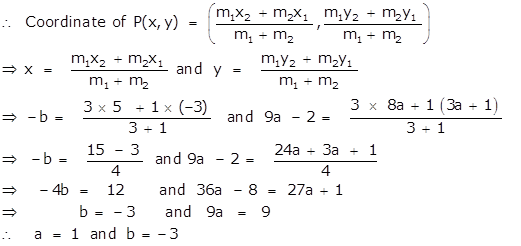
No comments:
Post a Comment