Find the equation of a line whose:
y-intercept = 2 and slope = 3.
Given, y-intercept = c = 2 and slope = m = 3.
Substituting the values of c and m in the equation y = mx + c, we get,
y = 3x + 2, which is the required equation.
Find the equation of a line whose:
y-intercept = -1 and inclination = 45o.
Given, y-intercept = c = -1 and inclination = 45o.
Slope = m = tan 45o = 1
Substituting the values of c and m in the equation y = mx + c, we get,
y = x - 1, which is the required equation.
Find the equation of the line whose slope is ![]() and which passes through (-3, 4).
and which passes through (-3, 4).
Given, slope = ![]()
The equation passes through (-3, 4) = (x1, y1)
Substituting the values in y - y1 = m(x - x1), we get,
y - 4 = ![]() (x + 3)
(x + 3)
3y - 12 = -4x - 12
4x + 3y = 0, which is the required equation.
Find the equation of a line which passes through (5, 4) and makes an angle of 60o with the positive direction of the x-axis.
Slope of the line = tan 60o = ![]()
The line passes through the point (5, 4) = (x1, y1)
Substituting the values in y - y1 = m(x - x1), we get,
y - 4 = ![]() (x - 5)
(x - 5)
y - 4 = ![]() x - 5
x - 5![]()
y =![]() x + 4 - 5
x + 4 - 5![]() , which is the required equation.
, which is the required equation.
Find the equation of the line passing through:
(i) (0, 1) and (1, 2) (ii) (-1, -4) and (3, 0)
(i) Let (0, 1) = (x1, y1) and (1, 2) = (x2, y2)
![]()
The required equation of the line is given by:
y - y1 = m(x - x1)
y - 1 = 1(x - 0)
y - 1 = x
y = x + 1
(ii) Let (-1, -4) = (x1, y1) and (3, 0) = (x2, y2)
![]()
The required equation of the line is given by:
y - y1 = m(x - x1)
y + 4 = 1(x + 1)
y + 4 = x + 1
y = x - 3
The co-ordinates of two points P and Q are (2, 6) and (-3, 5) respectively. Find:
(i) the gradient of PQ;
(ii) the equation of PQ;
(iii) the co-ordinates of the point where PQ intersects the x-axis.
Given, co-ordinates of two points P and Q are (2, 6) and (-3, 5) respectively.
(i) Gradient of PQ = ![]()
(ii) The equation of the line PQ is given by:
y - y1 = m(x - x1)
y - 6 = ![]() (x - 2)
(x - 2)
5y - 30 = x - 2
5y = x + 28
(iii) Let the line PQ intersects the x-axis at point A (x, 0).
Putting y = 0 in the equation of the line PQ, we get,
0 = x + 28
x = -28
Thus, the co-ordinates of the point where PQ intersects the x-axis are A (-28, 0).
The co-ordinates of two points A and B are (-3, 4) and (2, -1). Find:
(i) the equation of AB;
(ii) the co-ordinates of the point where the line AB intersects the y-axis.
(i) Given, co-ordinates of two points A and B are (-3, 4) and (2, -1).
Slope =![]()
The equation of the line AB is given by:
y - y1 = m(x - x1)
y + 1 = -1(x - 2)
y + 1 = -x + 2
x + y = 1
(ii) Let the line AB intersects the y-axis at point (0, y).
Putting x = 0 in the equation of the line, we get,
0 + y = 1
y = 1
Thus, the co-ordinates of the point where the line AB intersects the y-axis are (0, 1).
The figure given below shows two straight lines AB and CD intersecting each other at point P (3, 4). Find the equation of AB and CD.

Slope of line AB = tan 45o = 1
The line AB passes through P (3, 4). So, the equation of the line AB is given by:
y - y1 = m(x - x1)
y - 4 = 1(x - 3)
y - 4 = x - 3
y = x + 1
Slope of line CD = tan 60o = ![]()
The line CD passes through P (3, 4). So, the equation of the line CD is given by:
y - y1 = m(x - x1)
y - 4 = ![]() (x - 3)
(x - 3)
y - 4 = ![]() x - 3
x - 3 ![]()
y = ![]() x + 4 - 3
x + 4 - 3 ![]()
In ΔABC, A = (3, 5), B = (7, 8) and C = (1, -10). Find the equation of the median through A.
The following figure shows a parallelogram ABCD whose side AB is parallel to the x-axis, ![]() A = 60o and vertex C = (7, 5). Find the equations of BC and CD.
A = 60o and vertex C = (7, 5). Find the equations of BC and CD.
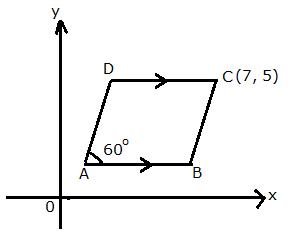
Since, ABCD is a parallelogram,
![]()
![]() B = 180o - 60o = 120o
B = 180o - 60o = 120o
Slope of BC = tan 120o = tan (90o + 30o) = cot30o = ![]()
Equation of the line BC is given by:
y - y1 = m(x - x1)
y - 5 = ![]() (x - 7)
(x - 7)
y - 5 = ![]() x - 7
x - 7![]()
y = ![]() x + 5 - 7
x + 5 - 7![]()
Since, CD || AB and AB || x-axis, slope of CD = Slope of AB = 0
Equation of the line CD is given by:
y - y1 = m(x - x1)
y - 5 = 0(x - 7)
y = 5
Find the equation of the straight line passing through origin and the point of intersection of the lines x + 2y = 7 and x - y = 4.
The given equations are:
x + 2y = 7 ....(1)
x - y = 4 ....(2)
Subtracting (2) from (1), we get,
3y = 3
y = 1
From (2), x = 4 + y = 4 + 1 = 5
The required line passes through (0, 0) and (5, 1).
![]()
Required equation of the line is given by:

In triangle ABC, the co-ordinates of vertices A, B and C are (4, 7), (-2, 3) and (0, 1) respectively. Find the equation of median through vertex A.
Also, find the equation of the line through vertex B and parallel to AC.
Given, the co-ordinates of vertices A, B and C of a triangle ABC are (4, 7), (-2, 3) and (0, 1) respectively.
Let AD be the median through vertex A.
Co-ordinates of the point D are
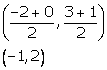
![]() Slope of AD =
Slope of AD = ![]()
The equation of the median AD is given by:
y - y1 = m(x - x1)
y - 2 = 1(x + 1)
y - 2 = x + 1
y = x + 3
The slope of the line which is parallel to line AC will be equal to the slope of AC.
Slope of AC = ![]()
The equation of the line which is parallel to AC and passes through B is given by:
y - 3 = ![]() (x + 2)
(x + 2)
2y - 6 = 3x + 6
2y = 3x + 12
A, B and C have co-ordinates (0, 3), (4, 4) and (8, 0) respectively. Find the equation of the line through A and perpendicular to BC.
Slope of BC = ![]()
Slope of line perpendicular to BC = ![]()
The equation of the line through A and perpendicular to BC is given by:
y - y1 = m(x - x1)
y - 3 = 1(x - 0)
y - 3 = x
y = x + 3
Find the equation of the perpendicular dropped from the point (-1, 2) onto the line joining the points (1, 4) and (2, 3).
Let A = (1, 4), B = (2, 3), and C = (-1, 2).
Slope of AB = ![]()
Slope of equation perpendicular to AB = ![]()
The equation of the perpendicular drawn through C onto AB is given by:
y - y1 = m(x - x1)
y - 2 = 1(x + 1)
y - 2 = x + 1
y = x + 3
Find the equation of the line, whose:
(i) x-intercept = 5 and y-intercept = 3
(ii) x-intercept = -4 and y-intercept = 6
(iii) x-intercept = -8 and y-intercept = -4
(i) When x-intercept = 5, corresponding point on x-axis is (5, 0)
When y-intercept = 3, corresponding point on y-axis is (0, 3).
Let (x1, y1) = (5, 0) and (x2, y2) = (0, 3)
Slope = ![]()
The required equation is:
y - y1 = m(x - x1)
y - 0 = ![]() (x - 5)
(x - 5)
5y = -3x + 15
3x + 5y = 15
(ii) When x-intercept = -4, corresponding point on x-axis is (-4, 0)
When y-intercept = 6, corresponding point on y-axis is (0, 6).
Let (x1, y1) = (-4, 0) and (x2, y2) = (0, 6)
Slope = ![]()
The required equation is:
y - y1 = m(x - x1)
y - 0 = ![]() (x + 4)
(x + 4)
2y = 3x + 12
(iii) When x-intercept = -8, corresponding point on x-axis is (-8, 0)
When y-intercept = -4, corresponding point on y-axis is (0, -4).
Let (x1, y1) = (-8, 0) and (x2, y2) = (0, -4)
Slope = ![]()
The required equation is:
y - y1 = m(x - x1)
y - 0 = ![]() (x + 8)
(x + 8)
2y = -x - 8
x + 2y + 8 = 0
Find the equation of the line whose slope is ![]() and x-intercept is 6.
and x-intercept is 6.
Since, x-intercept is 6, so the corresponding point on x-axis is (6, 0).
Slope = m = ![]()
Required equation of the line is given by:
y - y1 = m(x - x1)
y - 0 = ![]() (x - 6)
(x - 6)
6y = -5x + 30
5x + 6y = 30
Find the equation of the line with x-intercept 5 and a point on it (-3, 2).
Since, x-intercept is 5, so the corresponding point on x-axis is (5, 0).
The line also passes through (-3, 2).
![]() Slope of the line =
Slope of the line = ![]()
Required equation of the line is given by:
y - y1 = m(x - x1)
y - 0 = ![]() (x - 5)
(x - 5)
4y = -x + 5
x + 4y = 5
Find the equation of the line through (1, 3) and making an intercept of 5 on the y-axis.
Since, y-intercept = 5, so the corresponding point on y-axis is (0, 5).
The line passes through (1, 3).
![]() Slope of the line =
Slope of the line = ![]()
Required equation of the line is given by:
y - y1 = m(x - x1)
y - 5 = -2(x - 0)
y - 5 = -2x
2x + y = 5
Find the equations of the lines passing through point (-2, 0) and equally inclined to the co-ordinate axis.
Let AB and CD be two equally inclined lines.
For line AB:
Slope = m = tan 45o = 1
(x1, y1) = (-2, 0)
Equation of the line AB is:
y - y1 = m(x - x1)
y - 0 = 1(x + 2)
y = x + 2
For line CD:
Slope = m = tan (-45o) = -1
(x1, y1) = (-2, 0)
Equation of the line CD is:
y - y1 = m(x - x1)
y - 0 = -1(x + 2)
y = -x - 2
x + y + 2 = 0
The line through P(5, 3) intersects y-axis at Q.
(i) Write the slope of the line.
(ii) Write the equation of the line.
(iii) Find the co-ordinates of Q.
(i)
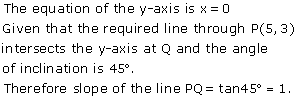
(ii)

(iii)

Write down the equation of the line whose gradient is ![]() and which passes through point P, where P divides the line segment joining A (4, -8) and B (12, 0) in the ratio 3: 1.
and which passes through point P, where P divides the line segment joining A (4, -8) and B (12, 0) in the ratio 3: 1.
Given, P divides the line segment joining A (4, -8) and B (12, 0) in the ratio 3: 1.
Co-ordinates of point P are

Slope = m =![]() (Given)
(Given)
Thus, the required equation of the line is
y - y1 = m(x - x1)
y + 2 = ![]() (x - 10)
(x - 10)
5y + 10 = -2x + 20
2x + 5y = 10
A (1, 4), B (3, 2) and C (7, 5) are vertices of a triangle ABC, Find:
(i) the co-ordinates of the centroid of triangle ABC.
(ii) the equation of a line, through the centroid and parallel to AB.
(i) Co-ordinates of the centroid of triangle ABC are
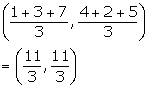
(ii) Slope of AB = ![]()
Slope of the line parallel to AB = Slope of AB = -1
Thus, the required equation of the line is
y - y1 = m(x - x1)
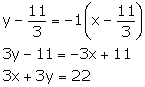
A (7, -1), B (4, 1) and C (-3, 4) are the vertices of a triangle ABC. Find the equation of a line through the vertex B and the point P in AC; such that AP: CP = 2: 3.
Given, AP: CP = 2: 3
![]() Co-ordinates of P are
Co-ordinates of P are

Slope of BP = ![]()
Required equation of the line passing through points B and P is
y - y1 = m(x - x1)
y - 1 = 0(x - 3)
y = 1
No comments:
Post a Comment