Chapter 20 - Cylinder, Cone and Sphere (Surface Area and Volume) Exercise Ex. 20(B)

Question 1

Find the volume of a cone whose slant height is 17 cm and radius of base is 8 cm.

Solution 1

Slant height () = 17 cm

Radius (r) = 8 cm

But,

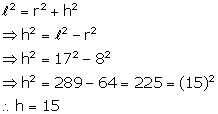
Now, volume of cone = 

Question 2

The curved surface area of a cone is  If the radius of its base is 56 cm, find its height.

Solution 2

Curved surface area = 

Radius of base (r) = 56 cm

Let slant height = 

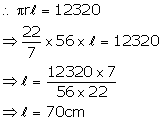
Height of the cone =

Question 3

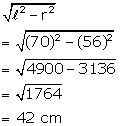
The circumference of the base of a 12 m high conical tent is 66 m. Find the volume of the air contained in it.

Solution 3

Circumference of the conical tent = 66 m

and height (h) = 12 m

Therefore, volume of air contained in it = 

Question 4

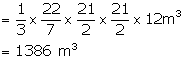
The radius and height of a right circular cone are in the ratio 5:12 and its volume is 2512 cubic cm. Find the radius and slant height of the cone. (Take 

Solution 4

The ratio between radius and height = 5:12

Volume = 5212 cubic cm

Let radius (r) = 5x, height (h) = 12x and slant height = 

Now Volume = 

Question 5

Two right circular cones x and y are made, x having three times the radius of y and y having half the volume of x. Calculate the ratio between the heights of x and y.

Solution 5

Let radius of cone y = r

Therefore, radius of cone x = 3r

Let volume of cone y = V

then volume of cone x = 2V

Let h₁ be the height of x and h2 be the height of y.

Therefore, Volume of cone = 

Volume of cone x = 

Volume of cone y = 

Question 6

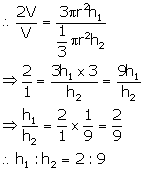
The diameters of two cones are equal. If their slant heights are in the ratio 5:4, find the ratio of their curved surface areas.

Solution 6

Let radius of each cone = r

Ratio between their slant heights = 5:4

Let slant height of the first cone = 5x

and slant height of second cone = 4x

Therefore, curved surface area of the first cone =

curved surface area of the second cone = 

Hence, ratio between them = 

Question 7

There are two cones. The curved surface area of one is twice that of the other. The slant height of the latter is twice that of the former. Find the ratio of their radii.

Solution 7

Let slant height of the first cone = 

then slant height of the second cone = 2

Radius of the first cone = 

Radius of the second cone = 

Then, curved surface area of first cone = 

curved surface area of second cone = 

According to given condition:

Question 8

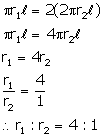
A heap of wheat is in the form of a cone of diameter 16.8 m and height 3.5 m. Find its volume. How much cloth is required to just cover the heap?

Solution 8

Diameter of the cone = 16.8 m

Therefore, radius (r) = 8.4 m

Height (h) = 3.5 m

(i) Volume of heap of wheat = 

(ii) Slant height () = 

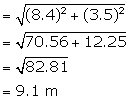
Therefore, cloth required or curved surface area = 

Question 9

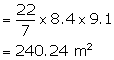
Find what length of canvas, 1.5 m in width, is required to make a conical tent 48 m in diameter and 7 m in height. Given that 10% of the canvas is used in folds and stitching. Also, find the cost of the canvas at the rate of Rs. 24 per meter.

Solution 9

Diameter of the tent = 48 m

Therefore, radius (r) = 24 m

Height (h) = 7 m

Slant height () = 

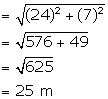
Curved surface area = 

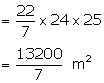
Canvas required for stitching and folding

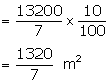
Total canvas required (area)

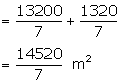
Length of canvas

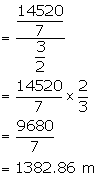
Rate = Rs 24 per meter

Total cost 

Question 10

A solid cone of height 8 cm and base radius 6 cm is melted and re-casted into identical cones, each of height 2 cm and diameter 1 cm. Find the number of cones formed.

Solution 10

Height of solid cone (h) = 8 cm

Radius (r) = 6 cm

Volume of solid cone = 

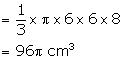
Height of smaller cone = 2 cm

and radius = 

Volume of smaller cone

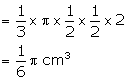
Number of cones so formed

Question 11

The total surface area of a right circular cone of slant height 13 cm is . Calculate:

(i) its radius in cm

(ii) its volume in cm³. Take 

Solution 11

Total surface area of cone = 

slant height (l) = 13 cm

(i) Let r be its radius, then

Total surface area = 

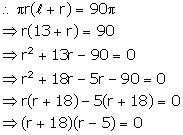
Either r+18 = 0, then r = -18 which is not possible

or r-5=0, then r = 5

Therefore, radius = 5 cm

(ii) Now

Question 12

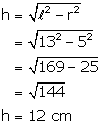
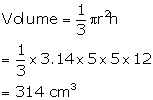
The area of the base of a conical solid is 38.5 cm² and its volume is 154 cm³. Find the curved surface area of the solid.

Solution 12

Question 13

A vessel, in the form of an inverted cone, is filled with water to the brim. Its height is 32 cm and diameter of the base is 25.2 cm. Six equal solid cones are dropped in it, so that they are fully submerged. As a result, one-fourth of water in the original cone overflows. What is the volume of each of the solid cones submerged?

Solution 13

Volume of vessel = volume of water = 

diameter = 25.2 cm, therefore radius = 12.6 cm

height = 32 cm

Volume of water in the vessel = 

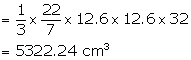
On submerging six equal solid cones into it, one-fourth of the water overflows.

Therefore, volume of the equal solid cones submerged

= Volume of water that overflows

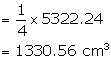
Now, volume of each cone submerged

Question 14

The volume of a conical tent is 1232 m³ and the area of the base floor is 154 m². Calculate the:

(i) radius of the floor

(ii) height of the tent

(iii) length of the canvas required to cover this conical tent if its width is 2 m.

Solution 14

(i) Let r be the radius of the base of the conical tent, then area of the base floor = 

Hence, radius of the base of the conical tent i.e. the floor = 7 m

(ii) Let h be the height of the conical tent, then the volume =

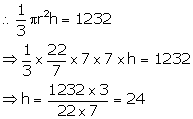
Hence, the height of the tent = 24 m

(iii) Let l be the slant height of the conical tent, then 

The area of the canvas required to make the tent = 

Length of the canvas required to cover the conical tent of its width 2 m =