Chapter 14 - Equation of a Line Exercise Ex. 14(D)

Question 1

Find the slope and y-intercept of the line:

(i) y = 4

(ii) ax - by = 0

(iii) 3x - 4y = 5

Solution 1

(i) y = 4

Comparing this equation with y = mx + c, we have:

Slope = m = 0

y-intercept = c = 4

(ii) ax - by = 0  by = ax  y = 

Comparing this equation with y = mx + c, we have:

Slope = m = 

y-intercept = c = 0

(iii) 3x - 4y = 5 

Comparing this equation with y = mx + c, we have:

Slope = m = 

y-intercept = c = 

Question 2

The equation of a line x - y = 4. Find its slope and y-intercept. Also, find its inclination.

Solution 2

Given equation of a line is x - y = 4

 y = x - 4

Comparing this equation with y = mx + c. We have:

Slope = m = 1

y-intercept = c = -4

Let the inclination be .

Slope = 1 = tan  = tan 45^o

Question 3

(i) Is the line 3x + 4y + 7 = 0 perpendicular to the line 28x - 21y + 50 = 0?

(ii) Is the line x - 3y = 4 perpendicular to the line 3x - y = 7?

(iii) Is the line 3x + 2y = 5 parallel to the line x + 2y = 1?

(iv) Determine x so that the slope of the line through (1, 4) and (x, 2) is 2.

Solution 3

(i) 3x + 4y + 7 = 0

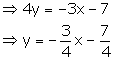
Slope of this line =

28x - 21y + 50 = 0

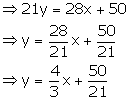
Slope of this line = 

Since, product of slopes of the two lines = -1, the lines are perpendicular to each other.

(ii) x - 3y = 4

3y = x - 4

y =

Slope of this line =

3x - y = 7

y = 3x - 7

Slope of this line = 3

Product of slopes of the two lines = 1 -1

So, the lines are not perpendicular to each other.

(iii) 3x + 2y = 5

2y = -3x + 5

y = 

Slope of this line = 

x + 2y = 1

2y = -x + 1

y = 

Slope of this line = 

Product of slopes of the two lines = 3 -1

So, the lines are not perpendicular to each other.

(iv) Given, the slope of the line through (1, 4) and (x, 2) is 2.

Question 4

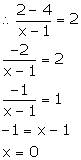
Find the slope of the line which is parallel to:

(i) x + 2y + 3 = 0 (ii) 

Solution 4

(i) x + 2y + 3 = 0

2y = -x - 3

y = 

Slope of this line = 

Slope of the line which is parallel to the given line = Slope of the given line = 

(ii) 

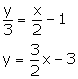
Slope of this line =

Slope of the line which is parallel to the given line = Slope of the given line = 

Question 5

Find the slope of the line which is perpendicular to:

(i)  (ii) 

Solution 5

(i) 

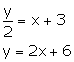
Slope of this line = 2

Slope of the line which is perpendicular to the given line = 

(ii) 

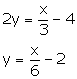
Slope of this line = 

Slope of the line which is perpendicular to the given line = 

Question 6

(i) Lines 2x - by + 5 = 0 and ax + 3y = 2 are parallel to each other. Find the relation connecting a and b.

(ii) Lines mx + 3y + 7 = 0 and 5x - ny - 3 = 0 are perpendicular to each other. Find the relation connecting m and n.

Solution 6

(i) 2x - by + 5 = 0

by = 2x + 5

Slope of this line =

 

ax + 3y = 2

3y = -ax + 2

y = 

Slope of this line =

Since, the lines are parallel, so the slopes of the two lines are equal.

 

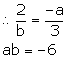
(ii) mx + 3y + 7 = 0

3y = -mx - 7

y = 

Slope of this line = 

 

5x - ny - 3 = 0

ny = 5x - 3

y = 

Slope of this line = 

Since, the lines are perpendicular; the product of their slopes is -1.

Question 7

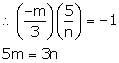
Find the value of p if the lines, whose equations are 2x - y + 5 = 0 and px + 3y = 4 are perpendicular to each other.

Solution 7

2x - y + 5 = 0

y = 2x + 5

Slope of this line = 2

px + 3y = 4

3y = -px + 4

y = 

Slope of this line = 

Since, the lines are perpendicular to each other, the product of the slopes is -1.

Question 8

The equation of a line AB is 2x - 2y + 3 = 0.

(i) Find the slope of the line AB.

(ii) Calculate the angle that the line AB makes with the positive direction of the x-axis.

Solution 8

(i) 2x - 2y + 3 = 0

2y = 2x + 3

y = x + 

Slope of the line AB = 1

(ii) Required angle = 

Slope = tan = 1 = tan 45^o

 = 45^o

Question 9

The lines represented by 4x + 3y = 9 and px - 6y + 3 = 0 are parallel. Find the value of p.

Solution 9

4x + 3y = 9

3y = -4x + 9

y =  + 3

Slope of this line = 

px - 6y + 3 = 0

6y = px + 3

y = 

Slope of this line = 

Since, the lines are parallel, their slopes will be equal.

Question 10

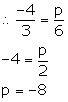
If the lines y = 3x + 7 and 2y + px = 3 are perpendicular to each other, find the value of p.

Solution 10

y = 3x + 7

Slope of this line = 3

2y + px = 3

2y = -px + 3

y = 

Slope of this line = 

Since, the lines are perpendicular to each other, the product of their slopes is -1.

Question 11

The line through A(-2,3) and B(4,b) is perpendicular to the line 2x - 4y =5. Find the value of b.

Solution 11

 

 

 

Question 12

Find the equation of the line through (-5, 7) and parallel to:

(i) x-axis (ii) y-axis

Solution 12

(i) The slope of the line parallel to x-axis is 0.

(x₁, y₁) = (-5, 7)

Required equation of the line is

y - y₁ = m(x - x₁)

y - 7 = 0(x + 5)

y = 7

(ii) The slope of the line parallel to y-axis is not defined.

That is slope of the line is  and hence the given line is parallel to y-axis.

(x₁, y₁) = (-5, 7)

Required equation of the line is

x - x₁ =0

x + 5=0

Question 13

(i) Find the equation of the line passing through (5, -3) and parallel to x - 3y = 4.

(ii) Find the equation of the line parallel to the line 3x + 2y = 8 and passing through the point (0, 1).

Solution 13

(i) x - 3y = 4

 3y = x - 4

 

Slope of this line = 

Slope of a line parallel to this line = 

Required equation of the line passing through (5, -3) is

y - y₁ = m(x - x₁)

y + 3 = (x - 5)

3y + 9 = x - 5

x - 3y - 14 = 0

(ii) 2y = -3x + 8

Or y = 

 Slope of given line = 

Since the required line is parallel to given straight line.

 Slope of required line (m) = 

Now the equation of the required line is given by:

y - y_{1 =} m(x - x₁)

y - 1 = 

2y - 2 = -3x

3x + 2y = 2

Question 14

Find the equation of the line passing through (-2, 1) and perpendicular to 4x + 5y = 6.

Solution 14

4x + 5y = 6

5y = -4x + 6

y = 

Slope of this line = 

The required line is perpendicular to the line 4x + 5y = 6.

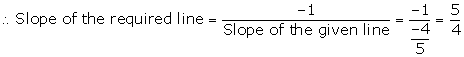
The required equation of the line is given by

y - y₁ = m(x - x₁)

y - 1 =  (x + 2)

4y - 4 = 5x + 10

5x - 4y + 14 = 0

Question 15

Find the equation of the perpendicular bisector of the line segment obtained on joining the points (6, -3) and (0, 3).

Solution 15

Let A = (6, -3) and B = (0, 3).

We know the perpendicular bisector of a line is perpendicular to the line and it bisects the line, that it, it passes through the mid-point of the line.

Co-ordinates of the mid-point of AB are

Thus, the required line passes through (3, 0).

Slope of AB = 

Slope of the required line = 

Thus, the equation of the required line is given by:

y - y₁ = m(x - x₁)

y - 0 = 1(x - 3)

y = x - 3

Question 16

In the following diagram, write down:

(i) the co-ordinates of the points A, B and C.

(ii) the equation of the line through A and parallel to BC.

Solution 16

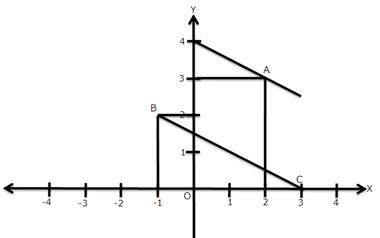
(i) The co-ordinates of points A, B and C are (2, 3), (-1, 2) and (3, 0) respectively.

(ii) Slope of BC = 

Slope of a line parallel to BC = Slope of BC = 

Required equation of a line passing through A and parallel to BC is given by

y - y₁ = m(x - x₁)

y - 3 =  (x - 2)

2y - 6 = -x + 2

X + 2y = 8

Question 17

B (-5, 6) and D (1, 4) are the vertices of rhombus ABCD. Find the equation of diagonal BD and of diagonal AC.

Solution 17

We know that in a rhombus, diagonals bisect each other at right angle.

Let O be the point of intersection of the diagonals AC and BD.

Co-ordinates of O are

Slope of BD = 

For line BD:

Slope = m = , (x₁, y₁) = (-5, 6)

Equation of the line BD is

y - y₁ = m(x - x₁)

y - 6 =  (x + 5)

3y - 18 = -x - 5

x + 3y = 13

For line AC:

Slope = m = , (x₁, y₁) = (-2, 5)

Equation of the line AC is

y - y₁ = m(x - x₁)

y - 5 = 3(x + 2)

y - 5 = 3x + 6

y = 3x + 11

Question 18

A = (7, -2) and C = (-1, -6) are the vertices of square ABCD. Find the equations of diagonal BD and of diagonal AC.

Solution 18

We know that in a square, diagonals bisect each other at right angle.

Let O be the point of intersection of the diagonals AC and BD.

Co-ordinates of O are

Slope of AC = 

For line AC:

Slope = m = , (x₁, y₁) = (7, -2)

Equation of the line AC is

y - y₁ = m(x - x₁)

y + 2 =  (x - 7)

2y + 4 = x - 7

2y = x - 11

For line BD:

Slope = m = 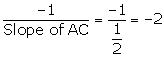, (x₁, y₁) = (3, -4)

Equation of the line BD is

y - y₁ = m(x - x₁)

y + 4 = -2(x - 3)

y + 4 = -2x + 6

2x + y = 2

Question 19

A (1, -5), B (2, 2) and C (-2, 4) are the vertices of triangle ABC, find the equation of:

(i) the median of the triangle through A.

(ii) the altitude of the triangle through B.

(iii) the line through C and parallel to AB.

Solution 19

(i) We know the median through A will pass through the mid-point of BC. Let AD be the median through A.

Co-ordinates of the mid-point of BC, i.e., D are

Slope of AD = 

Equation of the median AD is

y - 3 = -8(x - 0)

8x + y = 3

(ii) Let BE be the altitude of the triangle through B.

Slope of AC = 

Slope of BE = 

Equation of altitude BE is

y - 2 = (x - 2)

3y - 6 = x - 2

3y = x + 4

(iii) Slope of AB = 

Slope of the line parallel to AB = Slope of AB = 7

So, the equation of the line passing through C and parallel to AB is

y - 4 = 7(x + 2)

y - 4 = 7x + 14

y = 7x + 18

Question 20

(i) Write down the equation of the line AB, through (3, 2) and perpendicular to the line 2y = 3x + 5.

(ii) AB meets the x-axis at A and the y-axis at B. Write down the co-ordinates of A and B. Calculate the area of triangle OAB, where O is the origin.

Solution 20

(i) 2y = 3x + 5

Slope of this line = 

Slope of the line AB =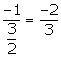 

(x₁, y₁) = (3, 2)

The required equation of the line AB is

y - y₁ = m(x - x₁)

y - 2 = (x - 3)

3y - 6 = -2x + 6

2x + 3y = 12

(ii) For the point A (the point on x-axis), the value of y = 0.

2x + 3y = 12  2x = 12  x = 6

Co-ordinates of point A are (6, 0).

For the point B (the point on y-axis), the value of x = 0.

2x + 3y = 12  3y = 12  y = 4

Co-ordinates of point B are (0, 4).

Area of OAB =  OA  OB =  6  4 = 12 sq units

Question 21

The line 4x - 3y + 12 = 0 meets the x-axis at A. Write the co-ordinates of A.

Determine the equation of the line through A and perpendicular to 4x - 3y + 12 = 0.

Solution 21

For the point A (the point on x-axis), the value of y = 0.

4x - 3y + 12 = 0  4x = -12  x = -3

Co-ordinates of point A are (-3, 0).

Here, (x₁, y₁) = (-3, 0)

The given line is 4x - 3y + 12 = 0

3y = 4x + 12

y = + 4

Slope of this line = 

Slope of a line perpendicular to the given line =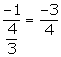 

Required equation of the line passing through A is

y - y₁ = m(x - x₁)

y - 0 = (x + 3)

4y = -3x - 9

3x + 4y + 9 = 0

Question 22

The point P is the foot of perpendicular from A (-5, 7) to the line whose equation is 2x - 3y + 18 = 0. Determine:

(i) the equation of the line AP

(ii) the co-ordinates of P

Solution 22

(i) The given equation is

2x - 3y + 18 = 0

3y = 2x + 18

y = x + 6

Slope of this line = 

Slope of a line perpendicular to this line =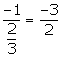 

(x₁, y₁) = (-5, 7)

The required equation of the line AP is given by

y - y₁ = m(x - x₁)

y - 7 = (x + 5)

2y - 14 = -3x - 15

3x + 2y + 1 = 0

(ii) P is the foot of perpendicular from point A.

So P is the point of intersection of the lines 2x - 3y + 18 = 0 and 3x + 2y + 1 = 0.

2x - 3y + 18 = 0  4x - 6y + 36 = 0

3x + 2y + 1 = 0  9x + 6y + 3 = 0

Adding the two equations, we get,

13x + 39 = 0

x = -3

3y = 2x + 18 = -6 + 18 = 12

y = 4

Thus, the co-ordinates of the point P are (-3, 4).

Question 23

The points A, B and C are (4, 0), (2, 2) and (0, 6) respectively. Find the equations of AB and BC.

If AB cuts the y-axis at P and BC cuts the x-axis at Q, find the co-ordinates of P and Q.

Solution 23

For the line AB:

(x₁, y₁) = (4, 0)

 

Equation of the line AB is

y - y₁ = m(x - x₁)

y - 0 = -1(x - 4)

y = -x + 4

x + y = 4 ....(1)

 

For the line BC:

(x₁, y₁) = (2, 2)

 

Equation of the line BC is

y - y₁ = m(x - x₁)

y - 2 = -2(x - 2)

y - 2 = -2x + 4

2x + y = 6 ....(2)

 

Given that AB cuts the y-axis at P. So, the abscissa of point P is 0.

Putting x = 0 in (1), we get,

y = 4

 

Thus, the co-ordinates of point P are (0, 4).

 

Given that BC cuts the x-axis at Q. So, the ordinate of point Q is 0.

Putting y = 0 in (2), we get,

2x = 6  x = 3

 

Thus, the co-ordinates of point Q are (3, 0).

Question 24

Match the equations A, B, C and D with lines L₁, L₂, L₃ and L₄, whose graphs are roughly drawn in the given diagram.

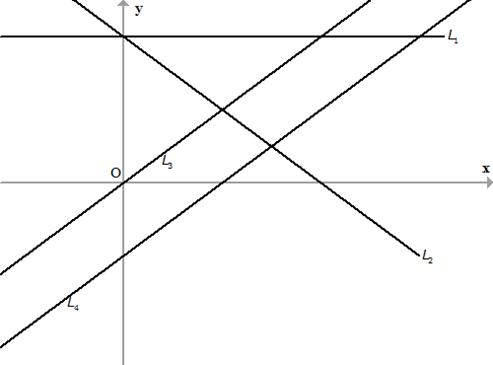
A  y = 2x; B  y - 2x + 2 = 0;

C  3x + 2y = 6; D  y = 2

Solution 24

Putting x = 0 and y = 0 in the equation y = 2x, we have:

LHS = 0 and RHS = 0

Thus, the line y = 2x passes through the origin.

Hence, A = L₃

Putting x = 0 in y - 2x + 2 = 0, we get, y = -2

Putting y = 0 in y - 2x + 2 = 0, we get, x = 1

So, x-intercept = 1 and y-intercept = -2

So, x-intercept is positive and y-intercept is negative.

Hence, B = L₄

Putting x = 0 in 3x + 2y = 6, we get, y = 3

Putting y = 0 in 3x + 2y = 6, we get, x = 2

So, both x-intercept and y-intercept are positive.

Hence, C = L₂

The slope of the line y = 2 is 0.

So, the line y = 2 is parallel to x-axis.

Hence, D = L₁

Question 25

Find the value of a for which the points A(a, 3), B(2, 1) and C(5, a) are collinear. Hence, find the equation of the line.

Solution 25