Chapter 18 - Tangents and Intersecting Chords Exercise Ex. 18(B)

Question 1

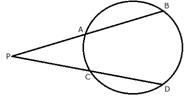
i) In the given figure, 3 x CP = PD = 9 cm and AP = 4.5 cm. Find BP.

ii) In the given figure, 5 x PA = 3 x AB = 30 cm and PC = 4cm. Find CD.

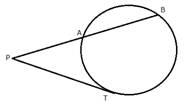
iii) In the given figure, tangent PT = 12.5 cm and PA = 10 cm; find AB.

Solution 1

i) Since two chords AB and CD intersect each other at P.

ii) Since two chords AB and CD intersect each other at P.

iii) Since PAB is the secant and PT is the tangent

Question 2

In the given figure, diameter AB and chord CD of a circle meet at P. PT is a tangent to the circle at T. CD = 7.8 cm, PD = 5 cm, PB = 4 cm. Find

(i) AB.

(ii) the length of tangent PT.

 

 

Solution 2

Question 3

In the following figure, PQ is the tangent to the circle at A, DB is a diameter and O is the centre of the circle. If ; calculate:

i) 

ii) 

iii) 

Solution 3

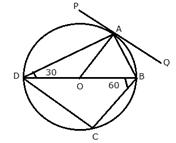
i) PAQ is a tangent and AB is the chord.

 (angles in the alternate segment)

ii) OA = OD (radii of the same circle)

iii) BD is the diameter.

 (angle in a semi-circle)

Now in 

Question 4

If PQ is a tangent to the circle at R; calculate:

i) 

ii) 

Given: O is the centre of the circle and 

Solution 4

PQ is a tangent and OR is the radius.

But in 

OT = OR (Radii of the same circle)

In 

Question 5

AB is diameter and AC is a chord of a circle with centre O such that angle BAC=30º. The tangent to the circle at C intersects AB produced in D. Show that BC = BD.

Solution 5

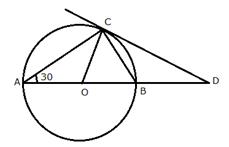
Join OC.

 (angles in alternate segment)

Arc BC subtends  at the centre of the circle and  at the remaining part of the circle.

Now in 

Now in 

Question 6

Tangent at P to the circumcircle of triangle PQR is drawn. If this tangent is parallel to side QR, show that triangle PQR is isosceles.

Solution 6

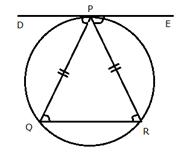
DE is the tangent to the circle at P.

DE||QR (Given)

Since the angle between a tangent and a chord through the point of contact is equal to the angle in the alternate segment

 (DE is tangent and PQ is chord)

from (i) and (ii)

Hence, triangle PQR is an isosceles triangle.

Question 7

Two circles with centers O and O' are drawn to intersect each other at points A and B.

Centre O of one circle lies on the circumference of the other circle and CD is drawn tangent to the circle with centre O' at A. Prove that OA bisects angle BAC.

Solution 7

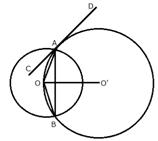
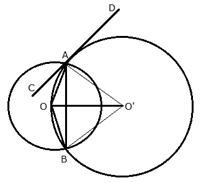
Join OA, OB, O'A, O'B and O'O.

CD is the tangent and AO is the chord.

 (angles in alternate segment)

In 

OA = OB (Radii of the same circle)

From (i) and (ii)

Therefore, OA is bisector of BAC

Question 8

Two circles touch each other internally at a point P. A chord AB of the bigger circle intersects the other circle in C and D. Prove that: 

Solution 8

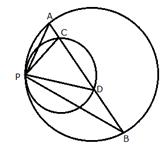
Draw a tangent TS at P to the circles given.

Since TPS is the tangent, PD is the chord.

Subtracting (i) from (ii)

But in 

Question 9

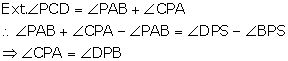
In a cyclic quadrilateral ABCD, the diagonal AC bisects the angle BCD. Prove that the diagonal BD is parallel to the tangent to the circle at point A.

Solution 9

TAS is a tangent and AB is a chord

But these are alternate angles

Therefore, TS||BD.

Question 10

In the figure, ABCD is a cyclic quadrilateral with BC = CD. TC is tangent to the circle at point C and DC is produced to point G. If angle BCG=108 and O is the centre of the circle, find:

i) angle BCT

ii) angle DOC

Solution 10

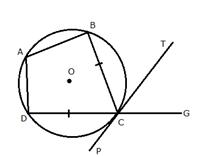
Join OC, OD and AC.

i)

ii)

PCT is a tangent and CA is a chord.

But arc DC subtends  at the centre and  at the

remaining part of the circle.

Question 11

Two circles intersect each other at point A and B. A straight line PAQ cuts the circle at P and Q. If the tangents at P and Q intersect at point T; show that the points P, B, Q and T are concyclic.

Solution 11

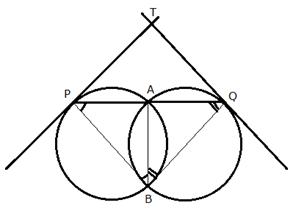
Join AB, PB and BQ

TP is the tangent and PA is a chord

 (angles in alternate segment)

Similarly,

Adding (i) and (ii)

But they are the opposite angles of the quadrilateral

Therefore, PBQT are cyclic.

Hence, P, B, Q and T are concyclic.

Question 12

In the figure, PA is a tangent to the circle. PBC is a secant and AD bisects angle BAC.

Show that the triangle PAD is an isosceles triangle. Also show that:

Solution 12

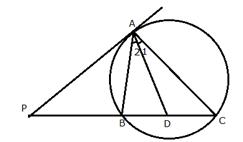
i) PA is the tangent and AB is a chord

 ( angles in the alternate segment)

AD is the bisector of 

In 

Therefore, is an isosceles triangle.

ii) In 

Question 13

Two circles intersect each other at point A and B. Their common tangent touches the circles at points P and Q as shown in the figure. Show that the angles PAQ and PBQ are supplementary.

Solution 13

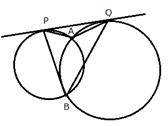
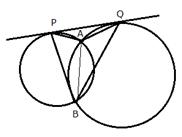
Join AB.

PQ is the tangent and AB is a chord

 (angles in alternate segment)

Similarly,

Adding (i) and (ii)

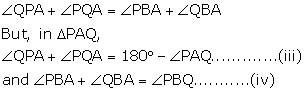
From (iii) and (iv)

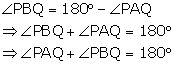
Hence,  and  are supplementary.

Question 14

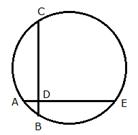
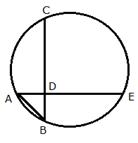
In the figure, chords AE and BC intersect each other at point D.

i) if , AB = 5 cm, BD = 4 cm and CD = 9 cm; find DE

ii) If AD = BD, Show that AE = BC.

Solution 14

Join AB.

i) In Rt. 

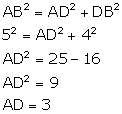
Chords AE and CB intersect each other at D inside the circle

AD x DE = BD x DC

3 x DE = 4 x 9

DE = 12 cm

ii) If AD = BD .......(i)

We know that:

AD x DE = BD x DC

But AD = BD

Therefore, DE = DC .......(ii)

Adding (i) and (ii)

AD + DE = BD + DC

Therefore, AE = BC

Question 15

Circles with centers P and Q intersect at points A and B as shown in the figure. CBD is a line segment and EBM is tangent to the circle, with centre Q, at point B. If the circles are congruent; show that CE = BD.

Solution 15

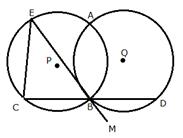
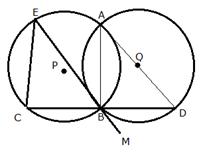
Join AB and AD

EBM is a tangent and BD is a chord.

 (angles in alternate segments)

 (Vertically opposite angles)

Since in the same circle or congruent circles, if angles are equal, then chords opposite to them are also equal.

Therefore, CE = BD

Question 16

In the adjoining figure, O is the centre of the circle and AB is a tangent to it at point B.  Find 

Solution 16

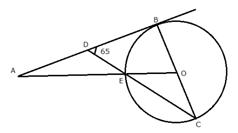
AB is a straight line.

AB i.e. DB is tangent to the circle at point B and BC is the diameter.

Now, OE = OC (radii of the same circle)

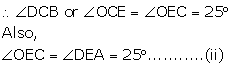
(vertically opposite angles)

In