Chapter 25 - Probability Exercise Ex. 25(A)

Question 1

A coin is tossed once. Find the probability of:

(i) getting a tail

(ii) not getting a tail

Solution 1

Sample Space = {H, T}

n(S) = 2

(i) A = Event of getting a tail = {T}

n(A)= 1

Therefore, the probability of getting a tail = 

(ii) Not getting a tail

Since P(getting a tail) + P(not getting a tail) = 1

→ P(not getting a tail) = 1 - (1/2) = 1/2

Question 2

A bag contains 3 white, 5 black and 2 red balls, all of the same shape and size. A ball is drawn from the bag without looking into it, find the probability that the ball drawn is:

(i) a black ball.

(ii) a red ball.

(iii) a white ball.

(iv) not a red ball.

(v) not a black ball.

Solution 2

Total number of balls = 3 + 5 + 2 = 10 

Total number of possible outcomes = 10

(i) There are 5 black balls

Number of favourable outcomes  = 5

Hence, P(getting a black ball) =  5/10 = 1/2

(ii) There are 2 red balls

 

Number of favourable outcomes  = 2

 

Hence, P(getting a red ball) =  2/10 = 1/5

 

(iii)

There are 3 white balls

Number of favourable outcomes  = 3

Hence, P(getting a white ball) =  3/10 = 3/10

 

(iv) There are 3 + 5 = 8 balls which are not red

 

Number of favourable outcomes  = 8

 

Hence, P(getting a white ball) =  8/10 = 4/5

 

(v) There are 3 + 2 = 5 balls which are not black

 

Number of favourable outcomes  = 5

 

Hence, P(getting a white ball) =  5/10 = 1/2

Question 3

In a single throw of a die, find the probability of getting a number:

(i) greater than 4.

(ii) less than or equal to 4.

(iii) not greater than 4.

Solution 3

Sample space = {1, 2, 3, 4, 5, 6}

n(s) = 6

(i) E = event of getting a number greater than 4 = {5, 6}

n (E) = 2

Probability of getting a number greater than 4 = 

(ii) E=event of getting a number less than or equal to 4={1, 2, 3, 4}

n(E) = 4

Probability of getting a number less than or equal to 4 = 

(iii) E=event of getting a number not greater than 4={1, 2, 3, 4}

n(E) = 4

Probability of getting a number not greater than 4 = 

Question 4

In a single throw of a die, find the probability that the number:

(i) will be an even number.

(ii) will not be an even number.

(iii) will be an odd number.

Solution 4

Sample space = {1, 2, 3, 4, 5, 6}

n(s) = 6

(i) E = event of getting an even number = {2, 4, 6}

n(E) = 3

Probability of a getting an even number = 

(ii) E = event of not getting an even number = {1, 3, 5}

n(E) = 3

Probability of a not getting an even number = 

(iii) E = event of getting an odd number = {1, 3, 5}

n(E) = 3

Probability of a getting an odd number = 

Question 5

From a well shuffled deck of 52 cards, one card is drawn. Find the probability that the card drawn will:

(i) be a black card.

(ii) not be a red card.

(iii) be a red card.

(iv) be a face card.

(v) be a face card of red colour.

Solution 5

Total number of cards = 52

Total number of outcomes = 52

There are 13 cards of each type. The cards of heart and diamond are red in colour. Spade and diamond are black. So, there are 26 red cards and 26 black cards.

(i) Number of black cards in a deck = 26

The number of favourable outcomes for the event of drawing a black card = 26

Probability of drawing a black card = 26/52 = 1/2

(ii) Number of red cards in a deck = 26

Therefore, number of non-red(black) cards = 52 - 26 = 26

The number of favourable outcomes for the event of not drawing a red card = 26

Probability of not drawing a red card = 26/52 = 1/2

(iii) Number of red cards in a deck = 26

The number of favourable outcomes for the event of drawing a red card = 26

Probability of drawing a red card =26/52= 1/2

(iv) There are 52 cards in a deck of cards, and 12 of these cards are face cards (4 kings, 4 queens, and 4 jacks).

The number of favourable outcomes for the event of drawing a face card  = 12

Probability of drawing a face card =12/52= 3/13

(v) There are 26 red cards in a deck, and 6 of these cards are face cards (2 kings, 2 queens, and 2 jacks).

The number of favourable outcomes for the event of drawing a face card of red color = 6

Probability of drawing a red face card =6/52 = 3/26

Question 6

(i) If A and B are two complementary events then what is the relation between P(A) and P(B)?

(ii) If the probability of happening an event A is 0.46. What will be the probability of not happening of the event A?

Solution 6

(i) Two complementary events, taken together, include all the outcomes for an experiment and the sum of the probabilities of all outcomes is 1.

P(A) + P(B) = 1

(ii) P(A) = 0.46

Let P(B) be the probability of not happening of event A

We know,

P(A) + P(B) = 1

P(B) = 1 - P(A)

P(B) = 1 - 0.46

P(B) = 0.54

Hence the probability of not happening of event A is 0.54

Question 7

In a T.T. match between Geeta and Ritu, the probability of the winning of Ritu is 0.73. Find the probability of:

(i) winning of Geeta

(ii) not winning of Ritu

Solution 7

(i) Winning of Geeta is a complementary event to winning of Ritu

Therefore,

P(winning of Ritu) + P(winning of Geeta) = 1

P(winning of Geeta) = 1 - P(winning of Ritu)

P(winning of Geeta) = 1 - 0.73

P(winning of Geeta) = 0.27

(ii) Not winning of Ritu is a complementary event to winning of Ritu

Therefore,

P(winning of Ritu) + P(not winning of Ritu) = 1

P(not winning of Ritu) = 1 - P(winning of Ritu)

P(not winning of Ritu) = 1 - 0.73

P(not winning of Ritu) = 0.27

Question 8

In a race between Mahesh and John, the probability that John will lose the race is 0.54. Find the probability of:

(i) winning of Mahesh

(ii) winning of John

Solution 8

(i) But if John looses, Mahesh wins

Hence, probability of John losing the race = Probability of Mahesh winning the race since it is a race between these two only

Therefore, P(winning of Mahesh) = 0.54

(ii) P(winning of Mahesh) + P(winning of John) = 1

0.54 + P(winning of John) = 1

P(winning of John) = 1 - 0.54

P(winning of John) = 0.46

Question 9

(i) Write the probability of a sure event

(ii) Write the probability of an event when impossible

(iii) For an event E, write a relation representing the range of values of P(E)

Solution 9

(i) The probability of a sure event is 1 i.e. P(E) = 1 where 'E' is the sure event.

Proof: In a sure event n(E) = n(S)

[Since Number of elements in Event 'E' will be equal to the number of element in sample-space.]

By definition of Probability :

P(E) = n (E)/ n (S) = 1

P(E) = 1

(ii) The probability of an impossible event is '0' i.e. P (E) = 0

Proof: Since E has no element, n(E) = 0

From definition of Probability:

P(E) = n (E) / n(S) = 0 / n(S)

P(E) = 0

(iii) The probability of an event lies between '0' and '1'.

i.e. 0P(E) 1.

Proof: Let 'S' be the sample space and 'E' be the event.

Then

0n(E)n (S)

0 / n(S) n(E)/ n(S) n(S) / n(S)

or 0 P(E) 1

The number of elements in 'E' can't be less than '0' i.e. negative and greater than the number of elements in S.

Question 10

In a single throw of die, find the probability of getting:

(i) 5

(ii) 8

(iii) a number less than 8

(iv) a prime number

Solution 10

Sample space = {1, 2, 3, 4, 5, 6}

n(S) = 6

(i) E = event of getting a 5 on a throw of die = {5}

n(E) = 1

Probability of getting a 5 =P(E) = n(E)/n(S) = 1/6

(ii) There are only six possible outcomes in a single throw of a die. If we want to find probability of 8 to come up, then in that case number of possible or favourable outcome is 0 (zero)

n(E) = 0

Probability of getting a 8 =P(E) = n(E)/n(S)= 0/6 = 0

(iii) If we consider to find the probability of number less than 8, then all six cases are favourable

n(E) = 6

Probability of getting a number less than 8 =P(E) = n(E)/n(S) = 6/6 = 1

(iv) E = event of getting a prime number = {2, 3, 5}

n(E) = 3

Probability of getting a prime number =P(E) = n(E)/n(S)  = 3/6 = 1/2

Question 11

A die is thrown once. Find the probability of getting:

(i) an even number

(ii) a number between 3 and 8

(iii) an even number or a multiple of 3

Solution 11

Sample space = {1, 2, 3, 4, 5, 6}

n(S) = 6

(i) E = the possible even numbers = {2, 4, 6}

n(E) = 3

Probability of getting an even number =P(E) = n(E)/n(S) = 3/6 =1/2

(ii) E = the possible even numbers between 3 and 8 = {4, 5, 6}

n(E) = 3

Probability of getting an even number between 3 and 8 =P(E) = n(E)/n(S) = 3/6= 1/2

(iii) E = the event of getting an even number or a multiple of 3 = {2, 3, 4, 6}

n(E) = 4

Probability of getting an even number or a multiple of 3 =P(E) = 4/6= 2/3

Question 12

Which of the following cannot be the probability of an event?

(i) 

(ii) 2.7

(iii) 43%

(iv) -0.6

(v) -3.2

(vi) 0.35

Solution 12

The probability of an event lies between '0' and '1' i.e. 0P(E)1.

(i)

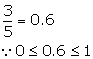
Hence, it can be the probability of an event.

(ii) 2.7

Hence, it cannot be the probability of an event.

(iii)

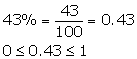
Hence, it can be the probability of an event.

(iv) -0.6

Hence, it cannot be the probability of an event.

(v) -3.2

Hence, it cannot be the probability of an event.

(vi) 0.35

Hence, it can be the probability of an event.

Question 13

A bag contains six identical black balls. A child withdraws one ball from the bag without looking into it. What is the probability that he takes out:

(i) a white ball

(ii) a black ball

Solution 13

Possible number of outcomes = 6 = number of balls in the bag

n(S) = 6

(i) E = event of drawing a white ball = number of white balls in the bag = 0

n(E) = 0

Probability of drawing a white ball =P(E) = n(E)/n(S)= 0/6 =0

(ii) E = event of drawing a black ball = number of black balls in the bag = 6

n(E) = 6

Probability of drawing a black ball =P(E)= n(E)/n(S)=6/6=1

Question 14

A single letter is selected at random from the word 'Probability'. Find the probability that it is a vowel.

Solution 14

Possible outcomes = S = {'P', 'r', 'o', 'b', 'a', 'b', 'i', 'l', 'i', 't', 'y'}

n(S) = 11

Event of selection of vowels = E = {'o', 'a', 'i', 'i'}

n(E) = 4

Probability of selection of a vowel = P(E)= n(E)/n(S) = 4/11

Question 15

Ramesh chooses a date at random in January for a party.

January
Mon		6	13	20	27
Tue		7	14	21	28
Wed	1	8	15	22	29
Thurs	2	9	16	23	30
Fri	3	10	17	24	31
Sat	4	11	18	25
Sun	5	12	19	26

 

Find the probability that he chooses:

(i) a Wednesday.

(ii) a Friday.

(iii) a Tuesday or a Saturday.

Solution 15

Number of possible outcomes = number of days in the month =31

n(S) = 31

(i) E = event of selection of a Wednesday = {1, 8, 15, 22, 29}

n(E) = 5

Probability of selection of a Wednesday =P(E) = n(E)/n(S)= 5/31

(ii) E = event of selection of a Friday = {3, 10, 17, 24, 31}

n(E) = 5

Probability of selection of a Friday =P(E) = n(E)/n(S)=5/31

(iii) E = event of selection of a Tuesday or a Saturday = {4, 7, 11, 14, 18, 21, 25, 28}

n(E) = 8

Probability of selection of a Tuesday or a Saturday =P(E) = n(E)/n(S)= 8/31