Evaluate:
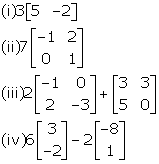

Find x and y if:
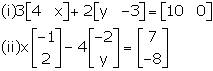
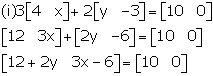
Comparing the corresponding elements, we get,
12 + 2y = 10 and 3x - 6 = 0
Simplifying, we get, y = -1 and x = 2.
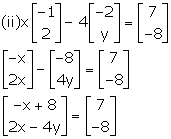
Comparing corresponding the elements, we get,
-x + 8 = 7 and 2x - 4y = -8
Simplifying, we get,
x = 1 and y = ![]() = 2.5
= 2.5
Given ![]() ; find:
; find:
(i) 2A - 3B + C
(ii) A + 2C - B
(i) 2A - 3B + C
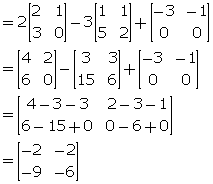
(ii) A + 2C - B
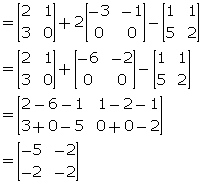
![]()
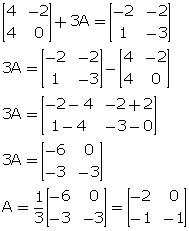
Given ![]()
(i) find the matrix 2A + B
(ii) find the matrix C such that:
C + B = ![]()
(i) ![]()
(ii) C + B = ![]()
C = ![]() - B =
- B = ![]()
If ![]() ; find the values of x, y and z.
; find the values of x, y and z.
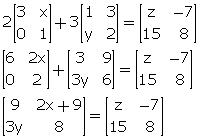
Comparing the corresponding elements, we get,
2x + 9 = -7 ![]() 2x = -16
2x = -16 ![]() x = -8
x = -8
3y = 15 ![]() y = 5
y = 5
z = 9
Given A = ![]() and At is its transpose matrix. Find:
and At is its transpose matrix. Find:
(i) 2A + 3At (ii) 2At - 3A
(iii) ![]() (iv)
(iv) ![]()
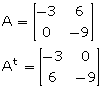
(i) 2A + 3At
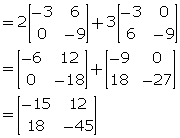
(ii) 2At - 3A
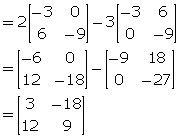
(iii) ![]()
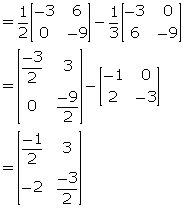
(iv) ![]()
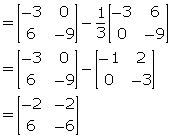
Given ![]()
Solve for matrix X:
(i) X + 2A = B
(ii) 3X + B + 2A = O
(iii) 3A - 2X = X - 2B.
(i) X + 2A = B
X = B - 2A
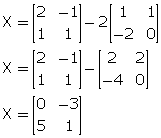
(ii) 3X + B + 2A = O
3X = -2A - B
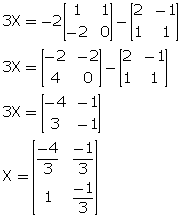
(iii) 3A - 2X = X - 2B
3A + 2B = X + 2X
3X = 3A + 2B
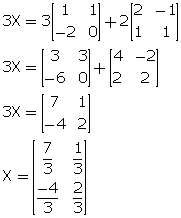
If ![]() , show that:
, show that:
3M + 5N = ![]()
3M + 5N
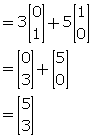
If I is the unit matrix of order 2 x 2; find the matrix M, such that:
(i) M - 2I = ![]()
(ii) 5M + 3I = ![]()
(i) M - 2I = ![]()
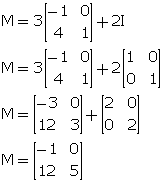
(ii) 5M + 3I = ![]()
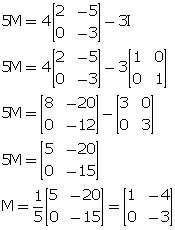
If ![]()
![]()
![]() 2M =
2M = ![]()
![]() M =
M = ![]()
No comments:
Post a Comment