Chapter 10 - Arithmetic Progression Exercise Ex. 10(F)

Question 1

The 6^th term of an A.P. is 16 and the 14^th term is 32. Determine the 36^th term.

Solution 1

Let 'a' be the first term and 'd' be the common difference of the given A.P.

Now, t₆ = 16 (given)

⇒ a + 5d = 16 ….(i)

And,

t₁₄ = 32 (given)

⇒ a + 13d = 32 ….(ii)

Subtracting (i) from (ii), we get

8d = 16

⇒ d = 2

⇒ a + 5(2) = 16

⇒ a = 6

Hence, 36^th term = t₃₆ = a + 35d = 6 + 35(2) = 76

Question 2

If the third and the 9^th term of an A.P. be 4 and -8 respectively, find which term is zero?

Solution 2

 

Question 3

An A.P. consists of 50 terms of which 3^rd term is 12 and the last term is 106. Find the 29^th term of the A.P.

Solution 3

For a given A.P.,

Number of terms, n = 50

3^rd term, t₃ = 12

⇒ a + 2d = 12 ….(i)

Last term, l = 106

⇒ t₅₀ = 106

⇒ a + 49d = 106 ….(ii)

Subtracting (i) from (ii), we get

47d = 94

⇒ d = 2

⇒ a + 2(2) = 12

⇒ a = 8

Hence, t₂₉ = a + 28d = 8 + 28(2) = 8 + 56 = 64

Question 4

Find the arithmetic mean of:

(i) -5 and 41

(ii) 3x - 2y and 3x + 2y

(iii) (m + n)² and (m - n)² 

Solution 4

Question 5

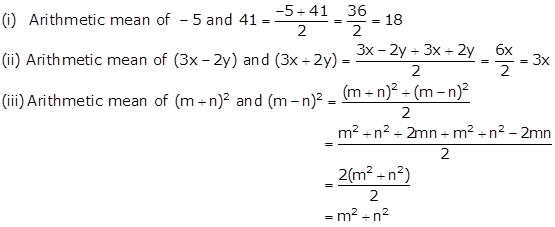
Find the sum of first 10 terms of the A.P.

4 + 6 + 8 + ……

Solution 5

Here,

First term, a = 4

Common difference, d = 6 - 4 = 2

n = 10

Question 6

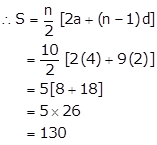
Find the sum of first 20 terms of an A.P. whose first term is 3 and the last term is 57.

Solution 6

Here,

First term, a = 3

Last term, l = 57

n = 20

Question 7

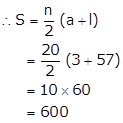
How many terms of the series 18 + 15 + 12 + …….. when added together will give 45?

Solution 7

Here, we find that

15 - 18 = 12 - 15 = -3

Thus, the given series is an A.P. with first term 18 and common difference -3.

Let the number of term to be added be 'n'.

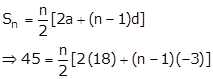
⇒ 90 = n[36 - 3n + 3]

⇒ 90 = n[39 - 3n]

⇒ 90 = 3n[13 - n]

⇒ 30 = 13n - n²

⇒ n² - 13n + 30 = 0

⇒ n² - 10n - 3n + 30 = 0

⇒ n(n - 10) - 3(n - 10) = 0

⇒ (n - 10)(n - 3) = 0

⇒ n - 10 = 0 or n - 3 = 0

⇒ n = 10 or n = 3

Thus, required number of term to be added is 3 or 10.

Question 8

The n^th term of a sequence is 8 - 5n. Show that the sequence is an A.P.

Solution 8

t_n = 8 - 5n

Replacing n by (n + 1), we get

t_n+1 = 8 - 5(n + 1) = 8 - 5n - 5 = 3 - 5n

Now,

t_n+1 - t_n = (3 - 5n) - (8 - 5n) = -5

Since, (t_n+1 - t_n) is independent of n and is therefore a constant.

Hence, the given sequence is an A.P.

Question 9

Find the general term (n^th term) and 23^rd term of the sequence 3, 1, -1, -3, ….. .

Solution 9

The given sequence is 1, -1, -3, …..

Now,

1 - 3 = -1 - 1 = -3 - (-1) = -2

Hence, the given sequence is an A.P. with first term a = 3 and common difference d = -2.

The general term (n^th term) of an A.P. is given by

t_n = a + (n - 1)d

= 3 + (n - 1)(-2)

= 3 - 2n + 2

= 5 - 2n

Hence, 23^rd term = t₂₃ = 5 - 2(23) = 5 - 46 = -41

Question 10

Which term of the sequence 3, 8, 13, ........ is 78?

Solution 10

The given sequence is 3, 8, 13, …..

Now,

8 - 3 = 13 - 8 = 5

Hence, the given sequence is an A.P. with first term a = 3 and common difference d = 5.

Let the n^th term of the given A.P. be 78.

⇒ 78 = 3 + (n - 1)(5)

⇒ 75 = 5n - 5

⇒ 5n = 80

⇒ n = 16

Thus, the 16^th term of the given sequence is 78.

Question 11

Is -150 a term of 11, 8, 5, 2, ....... ?

Solution 11

The given sequence is 11, 8, 5, 2, …..

Now,

8 - 11 = 5 - 8 = 2 - 5 = -3

Hence, the given sequence is an A.P. with first term a = 11 and common difference d = -3.

The general term of an A.P. is given by

t_n = a + (n - 1)d

⇒ -150 = 11 + (n - 1)(-5)

⇒ -161 = -5n + 5

⇒ 5n = 166

The number of terms cannot be a fraction.

So, clearly, -150 is not a term of the given sequence. 

Question 12

How many two digit numbers are divisible by 3?

Solution 12

 

Question 13

How many multiples of 4 lie between 10 and 250?

Solution 13

Question 14

The sum of the 4^th and the 8^th terms of an A.P. is 24 and the sum of the sixth term and the tenth is 44. Find the first three terms of the A.P.

Solution 14

Question 15

The sum of first 14 terms of an A.P. is 1050 and its 14^th term is 140. Find the 20^th term.

Solution 15

Let 'a' be the first term and 'd' be the common difference of the given A.P.

Given,

S₁₄ = 1050

⇒ 7[2a + 13d] = 1050

⇒ 2a + 13d = 150 

⇒ a + 6.5d = 75 ….(i)

And, t₁₄ = 140

⇒ a + 13d = 140 ….(ii)

Subtracting (i) from (ii), we get

6.5d = 65

⇒ d = 10

⇒ a + 13(10) = 140

⇒ a = 10

Thus, 20^th term = t₂₀ = 10 + 19d = 10 + 19(10) = 200

Question 16

The 25^th term of an A.P. exceeds its 9^th term by 16. Find its common difference.

Solution 16

n^th term of an A.P. is given by t_n= a + (n - 1) d.

⇒ t₂₅  = a + (25 - 1)d = a + 24d and

 t₉ = a + (9 - 1)d = a + 8d

According to the condition in the question, we get

t₂₅ = t₉ + 16

⇒ a + 24d = a + 8d + 16

⇒ 16d = 16

⇒ d = 1

 

 

Question 17

For an A.P., show that:

(m + n)^th term + (m - n)^th term = 2 × m^thterm

Solution 17

Let a and d be the first term and common difference respectively.

⇒(m + n)^th term = a + (m + n - 1)d …. (i) and

(m - n)^th term = a + (m - n - 1)d …. (ii)

From (i) + (ii), we get

(m + n)^th term + (m - n)^th term

= a + (m + n - 1)d + a + (m - n - 1)d

= a + md + nd - d + a + md - nd - d

= 2a + 2md - 2d

= 2a + (m - 1)2d

= 2[ a + (m - 1)d]

= 2 × m^thterm

 

Hence proved.

 

 

Question 18

If the n^th term of the A.P. 58, 60, 62,.... is equal to the n^th term of the A.P. -2, 5, 12, …., find the value of n.

Solution 18

In the first A.P. 58, 60, 62,....

a = 58 and d = 2

t_n = a + (n - 1)d

⇒ t_n = 58 + (n - 1)2 …. (i)

In the first A.P. -2, 5, 12, ….

a = -2 and d = 7

t_n = a + (n - 1)d

⇒ t_n= -2 + (n - 1)7 …. (ii)

Given that the n^th term of first A.P is equal to the n^th term of the second A.P.

⇒58 + (n - 1)2 = -2 + (n - 1)7 … from (i) and (ii)

⇒58 + 2n - 2 = -2 + 7n - 7

⇒ 65 = 5n

⇒ n = 15

 

 

Question 19

Which term of the A.P. 105, 101, 97 … is the first negative term?

Solution 19

Here a = 105 and d = 101 - 105 = -4

Let a_n be the first negative term.

⇒ a_n < 0

⇒ a + (n - 1)d < 0

⇒ 105 + (n - 1)(-4)<0

⇒ 105 - 4n + 4 <0

⇒ 109 - 4n < 0

⇒ 109 <4n

⇒ 27.25 < n

The value of n = 28.

Therefore 28^th term is the first negative term of the given A.P.

 

 

Question 20

How many three digit numbers are divisible by 7?

Solution 20

The first three digit number which is divisible by 7 is 105 and the last digit which is divisible by 7 is 994.

This is an A.P. in which a = 105, d = 7 and t_n = 994.

We know that n^th term of A.P is given by

 t_n = a + (n - 1)d.

⇒ 994 = 105 + (n - 1)7

⇒ 889 = 7n - 7

⇒ 896 = 7n

⇒ n = 128

∴ There are 128 three digit numbers which are divisible by 7.

 

Question 21

Divide 216 into three parts which are in A.P. and the product of the two smaller parts is 5040.

Solution 21

Let the three parts of 216 in A.P be (a - d), a, (a + d).

⇒a - d + a + a + d = 216

⇒ 3a = 216

⇒ a = 72

Given that the product of the two smaller parts is 5040.

⇒a(a - d ) = 5040

⇒ 72(72 - d) = 5040

⇒ 72 - d = 70

⇒ d = 2

∴ a - d = 72 - 2 = 70, a = 72 and a + d = 72 + 2 = 74

Therefore the three parts of 216 are 70, 72 and 74.

Question 22

Can 2n² - 7 be the n^th term of an A.P? Explain.

Solution 22

We have 2n² - 7,

Substitute n = 1, 2, 3, … , we get

2(1)² - 7, 2(2)² - 7, 2(3)² - 7, 2(4)² - 7, ….

-5, 1, 11, ….

Difference between the first and second term = 1 - (-5) = 6

And Difference between the second and third term = 11 - 1 = 10

Here, the common difference is not same.

Therefore the n^th term of an A.P can't be 2n² - 7.

 

Question 23

Find the sum of the A.P., 14, 21, 28, …, 168.

Solution 23

Here a = 14 , d = 7 and t_n = 168

t_n = a + (n - 1)d

⇒ 168 = 14 + (n - 1)7

⇒ 154 = 7n - 7

⇒ 154 = 7n - 7

⇒ 161 = 7n

⇒ n = 23

We know that,

 

Therefore the sum of the A.P., 14, 21, 28, …, 168 is 2093. 

Question 24

The first term of an A.P. is 20 and the sum of its first seven terms is 2100; find the 31^st term of this A.P.

Solution 24

Here a = 20 and S₇ = 2100

We know that,

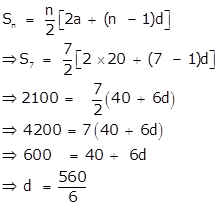
To find: t₃₁ =?

t_n = a + (n - 1)d

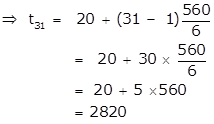
Therefore the 31^st term of the given A.P. is 2820. 

Question 25

Find the sum of last 8 terms of the A.P. -12, -10, -8, ……, 58.

Solution 25

First we will reverse the given A.P. as we have to find the sum of last 8 terms of the A.P.

58, …., -8, -10, -12.

Here a = 58 , d = -2

  

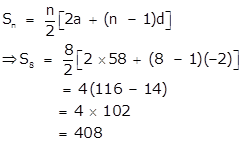
Therefore the sum of last 8 terms of the A.P. -12, -10, -8, ……, 58 is 408.