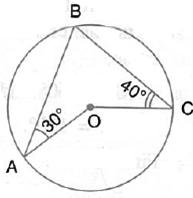
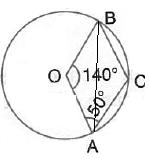
In the given figure, O is the centre of the circle. ![]() respectively. Find angle AOC Show your steps of working.
respectively. Find angle AOC Show your steps of working.


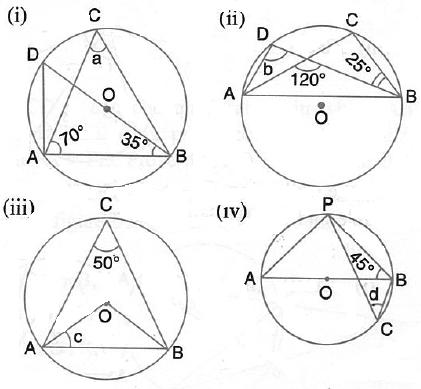
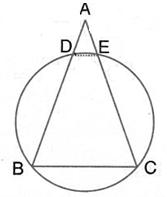
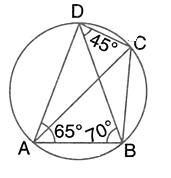
In the given figure, ∠BAD = 65°, ∠ABD = 70°, ∠BDC = 45°
(i) Prove that AC is a diameter of the circle.
(ii) Find ∠ACB.
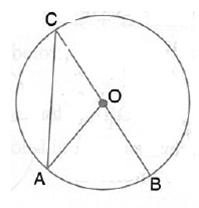
Given O is the centre of the circle and ![]() AOB = 70o.Calculate the value of:
AOB = 70o.Calculate the value of:
(i) ![]() OCA ; (ii)
OCA ; (ii) ![]() OAC.
OAC.


In each of the following figures, O is the centre of the circle. Find the values of a, b and c.
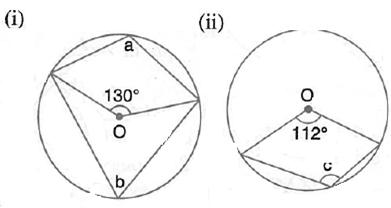


In each of the following figures, O is the centre of the circle. Find the values of a, b, c and d.


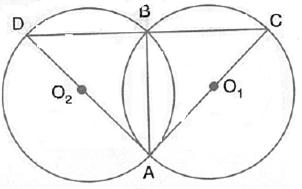
In the figure, AB is common chord of the two circles. If AC and AD are diameters; prove that D, B and C are in a straight line. O1 and O2 are the centres of two circles.

In the figure, given below, find:
![]() Show steps of your working.
Show steps of your working.


In the figure, given below, O is the centre of the circle. If
![]()

![]()


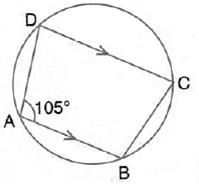
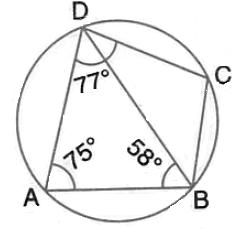
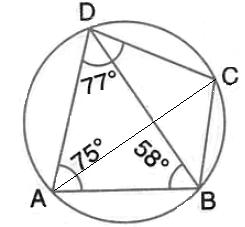
In the figure given below, ABCD is a cyclic quadrilateral in which ![]() BAD= 75o ;
BAD= 75o ; ![]() ABD= 58o and
ABD= 58o and ![]() ADC = 77o. Find:
ADC = 77o. Find:
(i) ![]() BDC, (ii)
BDC, (ii) ![]() BCD, (iii)
BCD, (iii) ![]() BCA.
BCA.

In the figure given below, O is the centre of the circle and triangle ABC is equilateral. Find:
(i) ![]() ADB, (ii)
ADB, (ii) ![]() AEB.
AEB.
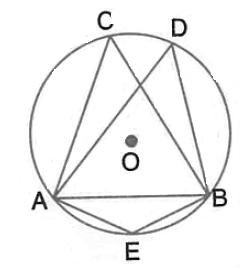


Given ![]() CAB = 75o and
CAB = 75o and ![]() CBA = 50o. Find the value of
CBA = 50o. Find the value of ![]() DAB +
DAB + ![]() ABD.
ABD.
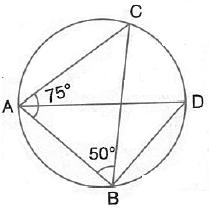


ABCD is a cyclic quadrilateral in a circle with centre O. If![]() ADC = 130o, find
ADC = 130o, find ![]() BAC.
BAC.


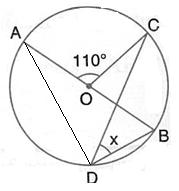
In the figure given alongside, AOB is a diameter of the circle and ![]() AOC = 110o, find
AOC = 110o, find ![]() BDC.
BDC.


In the following figure, O is the centre of the circle;![]() AOB = 60o and
AOB = 60o and ![]() BDC = 100o, find
BDC = 100o, find ![]() OBC.
OBC.
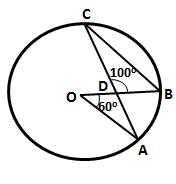


In ABCD is a cyclic quadrilateral in which![]() DAC = 27o,
DAC = 27o,![]() DBA = 50o and
DBA = 50o and ![]() ADB = 33o. Calculate (i)
ADB = 33o. Calculate (i) ![]() DBC, (ii)
DBC, (ii) ![]() DCB, (iii)
DCB, (iii)![]() CAB.
CAB.


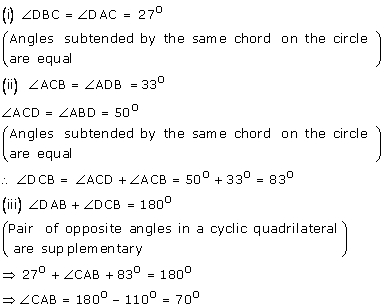
In the figure given alongside, AB and CD are straight lines through the centre O of a circle. If ![]() AOC = 80o and
AOC = 80o and ![]() CDE = 40o . Find the number of degrees in: (i)
CDE = 40o . Find the number of degrees in: (i) ![]() DCE; (ii)
DCE; (ii) ![]() ABC.
ABC.
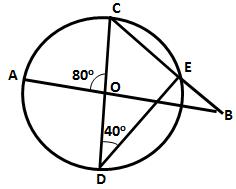


In the figure given below, AC is a diameter of a circle, whose centre is O. A circle is described on AO as diameter. AE, a chord of the larger circle, intersects the smaller circle at B. Prove that AB = BE.
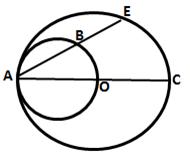


In the following figure,
(i) if ![]() BAD = 96o, find
BAD = 96o, find ![]() BCD and
BCD and ![]() BFE.
BFE.
(ii) Prove that AD is parallel to FE.



Prove that:
(i) the parallelogram, inscribed in a circle, is a rectangle.
(ii) the rhombus, inscribed in a circle, is a square.


In the following figure, AB = AC. Prove that DECB is an isosceles trapezium.


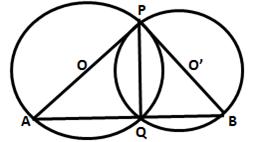
Two circles intersect at P and Q. Through P diameters PA and PB of the two circles are drawn. Show that the points A, Q and B are collinear.

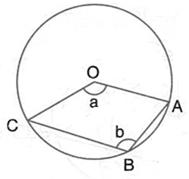
The figure given below, shows a circle with centre O. Given: ![]() AOC = a and
AOC = a and ![]() ABC = b.
ABC = b.
(i) Find the relationship between a and b
(ii) Find the measure of angle OAB, if OABC is a parallelogram.


Two chords AB and CD intersect at P inside the circle. Prove that the sum of the angles subtended by the arcs AC and BD as the centre O is equal to twice the angle APC


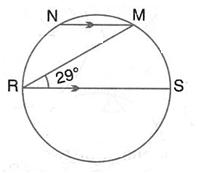
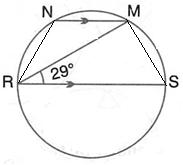
In the figure given RS is a diameter of the circle. NM is parallel to RS and ![]() MRS = 29o
MRS = 29o
Calculate : (i) ![]() RNM ; (ii)
RNM ; (ii) ![]() NRM.
NRM.

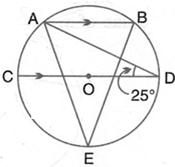
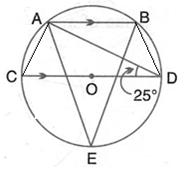
In the figure given alongside, AB || CD and O is the centre of the circle. If ![]() ADC = 25o; find the angle AEB. Give reasons in support of your answer.
ADC = 25o; find the angle AEB. Give reasons in support of your answer.

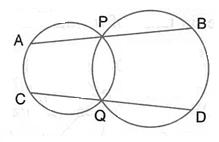
Two circles intersect at P and Q. Through P, a straight line APB is drawn to meet the circles in A and B. Through Q, a straight line is drawn to meet the circles at C and D. Prove that AC is parallel to BD.

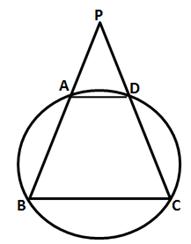
ABCD is a cyclic quadrilateral in which AB and DC on being produced, meet at P such that PA = PD. Prove that AD is parallel to BC.

AB is a diameter of the circle APBR as shown in the figure. APQ and RBQ are straight lines. Find:
![]()
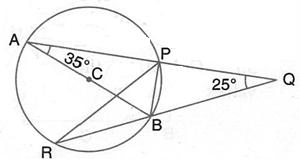


In the given figure, SP is the bisector of angle RPT and PQRS is a cyclic quadrilateral. Prove that: SQ = SR.
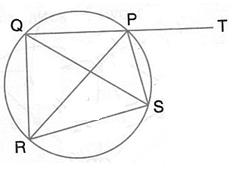


In the figure, O is the centre of the circle, ![]() AOE = 150o, DAO = 51o. Calculate the sizes of the angles CEB and OCE.
AOE = 150o, DAO = 51o. Calculate the sizes of the angles CEB and OCE.
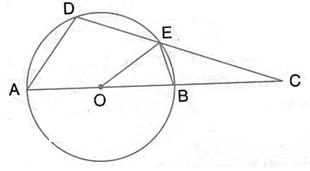


In the figure, P and Q are the centres of two circles intersecting at B and C. ACD is a straight line. Calculate the numerical value of x.
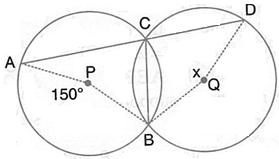


The figure shows two circles which intersect at A and B. The centre of the smaller circle is O and lies on the circumference of the larger circle. Given that ![]() APB = ao. Calculate, in terms of ao, the value of:
APB = ao. Calculate, in terms of ao, the value of:

Give reasons for your answers clearly.
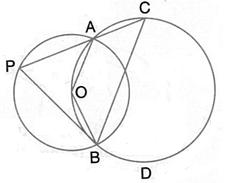


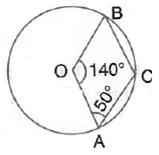
In the given figure, O is the centre of the circle and ![]() ABC = 55o. Calculate the values of x and y.
ABC = 55o. Calculate the values of x and y.
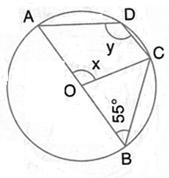


In the given figure, A is the centre of the circle, ABCD is a parallelogram and CDE is a straight line. Prove that ![]() BCD = 2
BCD = 2![]() ABE.
ABE.
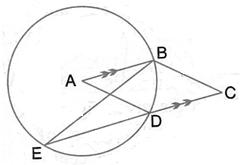


ABCD is a cyclic quadrilateral in which AB is parallel to DC and AB is a diameter of the circle. Given ![]() BED = 65o; calculate: (i)
BED = 65o; calculate: (i) ![]() DAB , (ii)
DAB , (ii) ![]() BDC.
BDC.
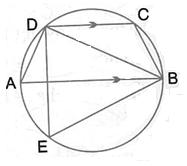

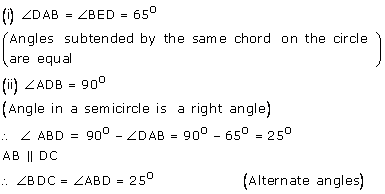
In the given figure, AB is a diameter of the circle. Chord ED is parallel to AB and ![]() EAB = 63o; calculate: (i)
EAB = 63o; calculate: (i) ![]() EBA , (ii)
EBA , (ii)![]() BCD.
BCD.
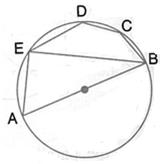

(i) ![]() AEB =
AEB = ![]()
(Angle in a semicircle is a right angle)
Therefore ![]() EBA =
EBA = ![]() -
- ![]() EAB =
EAB = ![]() -
- ![]() =
= ![]()
(ii) AB ![]() ED
ED
Therefore ![]() DEB = EBA =
DEB = EBA = ![]() (Alternate angles)
(Alternate angles)
Therefore BCDE is a cyclic quadrilateral
Therefore ![]() DEB +
DEB + ![]() BCD =
BCD = ![]()
[Pair of opposite angles in a cyclic quadrilateral are supplementary]
Therefore ![]() BCD =
BCD = ![]() -
- ![]() =
= ![]()
In the given figure, AB is a diameter of the circle with centre O. DO is parallel to CB and ![]() DCB = 120o; calculate:
DCB = 120o; calculate:
(i) ![]() DAB, (ii)
DAB, (ii) ![]() DBA, (iii)
DBA, (iii) ![]() DBC, (iv)
DBC, (iv) ![]() ADC.
ADC.
Also, show that the ![]() AOD is an equilateral triangle.
AOD is an equilateral triangle.
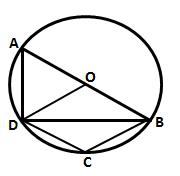


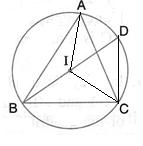
In the given figure, I is the incentre of the ![]() ABC. BI when produced meets the circumcirle of
ABC. BI when produced meets the circumcirle of ![]() ABC at D. Given
ABC at D. Given ![]() BAC = 55° and
BAC = 55° and ![]() ACB = 65o ; calculate: (i)
ACB = 65o ; calculate: (i) ![]() DCA, (ii)
DCA, (ii) ![]() DAC, (iii)
DAC, (iii) ![]() DCI, (iv)
DCI, (iv) ![]() AIC.
AIC.
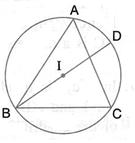

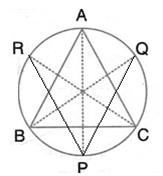
A triangle ABC is inscribed in a circle. The bisectors of angles BAC, ABC and ACB meet the circumcircle of the triangle at points P, Q and R respectively. Prove that:



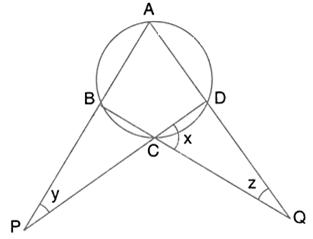
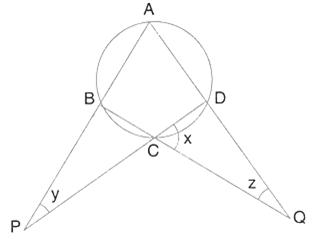
Calculate the angles x, y and z if: ![]()
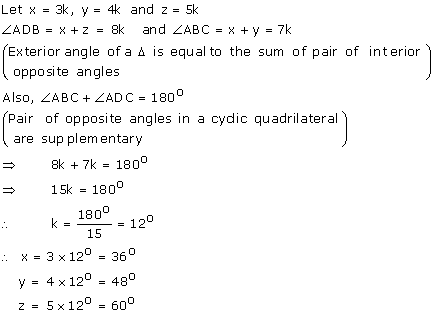
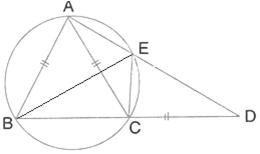
In the given figure, AB = AC = CD and ![]() ADC = 38o. Calculate:
ADC = 38o. Calculate:
(i) Angle ABC
(ii) Angle BEC.

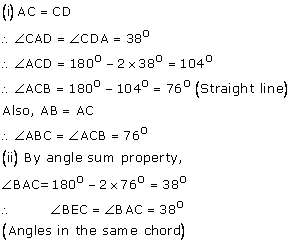
In the given figure, AC is the diameter of circle, centre O. Chord BD is perpendicular to AC. Write down the angles p, q and r in terms of x.


In the given figure, AC is the diameter of circle, centre O. CD and BE are parallel. Angle AOB = 80o and angle ACE = 10o. Calculate:
(i) Angle BEC ; (ii) Angle BCD ; (iii) Angle CED.
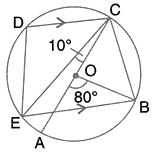


In the given figure, AE is the diameter of circle. Write down the numerical value of ![]() . Give reasons for your answer.
. Give reasons for your answer.
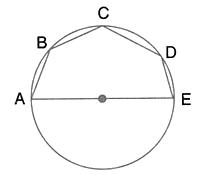

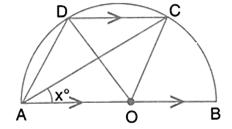
In the given figure, AOC is a diameter and AC is parallel to ED. If ![]() , calculate
, calculate ![]() .
.
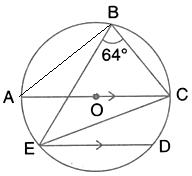

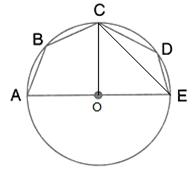
Use the given figure to find
![]() .
.
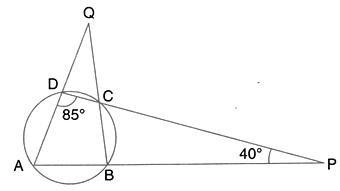


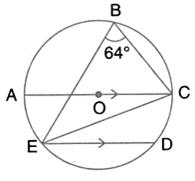
In the given figure, AOB is a diameter and DC is parallel to AB. If ![]() CAB = xo ; find (in terms of x) the values of:
CAB = xo ; find (in terms of x) the values of:
![]() .
.


In the given figure, AB is the diameter of a circle with centre O. ∠BCD = 130°. Find:
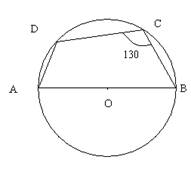
(i) ∠DAB (ii) ∠DBA
- ABCD is a cyclic quadrilateral
m∠DAB = 180° - ∠DCB
= 180° - 130°
= 50°
- In ∆ADB,
m∠DAB + m∠ADB + m∠DBA = 180°
⇒50° + 90° + m∠DBA = 180°
⇒m∠DBA = 40°
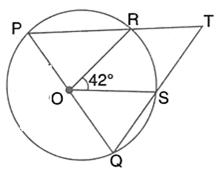
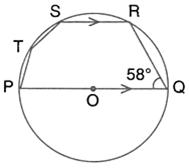
In the given figure, PQ is the diameter of the circle whose centre is O. Given![]() ROS =
ROS = ![]() ; calculate
; calculate ![]() RTS.
RTS.
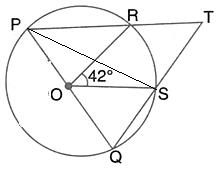

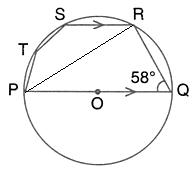
In the given figure, PQ is a diameter. Chord SR is parallel to PQ. Given that ![]() PQR =
PQR = ![]() ; calculate
; calculate
![]()

AB is the diameter of the circle with centre O. OD is parallel to BC and ![]() AOD =
AOD = ![]() ; calculate the numerical values of:
; calculate the numerical values of:
![]()
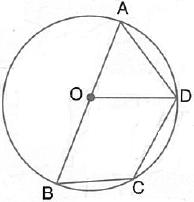


In the given figure, the centre O of the small circle lies on the circumference of the bigger circle. If ![]() APB =
APB = ![]() and
and ![]() BCD =
BCD = ![]() ; find:
; find:
![]()
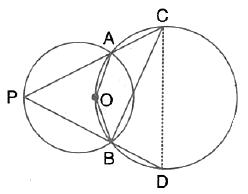
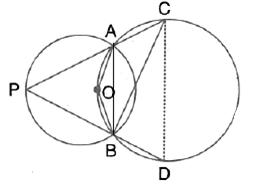

In the given figure, ![]() BAD =
BAD = ![]() ,
, ![]() ABD =
ABD = ![]() and
and ![]() BDC =
BDC = ![]() ; find:
; find:
![]()
Hence, show that AC is a diameter.


In a cyclic quadrilateral ABCD, ![]() A :
A :![]() C = 3 : 1 and
C = 3 : 1 and ![]() B :
B : ![]() D = 1 : 5; find each angle of the quadrilateral.
D = 1 : 5; find each angle of the quadrilateral.

The given figure shows a circle with centre O and![]() ABP =
ABP =![]() . Calculate the measure of
. Calculate the measure of
![]()

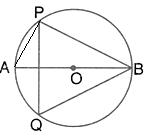

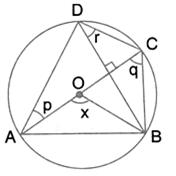
In the given figure, M is the centre of the circle. Chords AB and CD are perpendicular to each other. If ![]() MAD =x and
MAD =x and ![]() BAC = y,
BAC = y,

No comments:
Post a Comment