Point P divides the line segment joining the points A (8, 0) and B (16, -8) in the ratio 3: 5. Find its co-ordinates of point P.
Also, find the equation of the line through P and parallel to 3x + 5y = 7.
Using section formula, the co-ordinates of the point P are

3x + 5y = 7
![]()
Slope of this line = ![]()
As the required line is parallel to the line 3x + 5y = 7,
Slope of the required line = Slope of the given line =![]()
Thus, the equation of the required line is
y - y1 = m(x - x1)
y + 3 = ![]() (x - 11)
(x - 11)
5y + 15 = -3x + 33
3x + 5y = 18
The line segment joining the points A(3, -4) and B (-2, 1) is divided in the ratio 1: 3 at point P in it. Find the co-ordinates of P. Also, find the equation of the line through P and perpendicular to the line 5x - 3y = 4.
Using section formula, the co-ordinates of the point P are

The equation of the given line is
5x - 3y = 4

Slope of this line = ![]()
Since, the required line is perpendicular to the given line,
Slope of the required line = 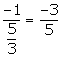
Thus, the equation of the required line is
y - y1 = m(x - x1)
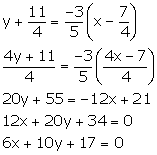
A line 5x + 3y + 15 = 0 meets y-axis at point P. Find the co-ordinates of point P. Find the equation of a line through P and perpendicular to x - 3y + 4 = 0.
Point P lies on y-axis, so putting x = 0 in the equation 5x + 3y + 15 = 0, we get, y = -5
Thus, the co-ordinates of the point P are (0, -5).
x - 3y + 4 = 0 ![]()
Slope of this line =![]()
The required equation is perpendicular to given equation x - 3y + 4 = 0.
![]() Slope of the required line =
Slope of the required line = 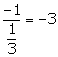
(x1, y1) = (0, -5)
Thus, the required equation of the line is
y - y1 = m(x - x1)
y + 5 = -3(x - 0)
3x + y + 5 = 0
Find the value of k for which the lines kx - 5y + 4 = 0 and 5x - 2y + 5 = 0 are perpendicular to each other.
kx - 5y + 4 = 0
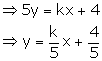
Slope of this line = m1 =![]()
5x - 2y + 5 = 0

Slope of this line = m2 =![]()
Since, the lines are perpendicular, m1m2 = -1
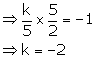
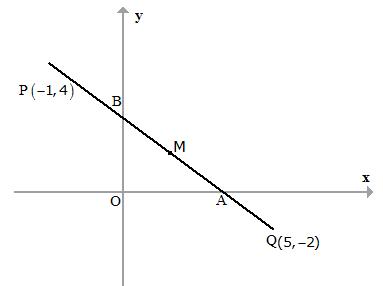
A straight line passes through the points P (-1, 4) and Q (5, -2). It intersects the co-ordinate axes at points A and B. M is the mid-point of the segment AB. Find:
(i) the equation of the line.
(ii) the co-ordinates of A and B.
(iii) the co-ordinates of M.
(i) Slope of PQ = ![]()
Equation of the line PQ is given by
y - y1 = m(x - x1)
y - 4 = -1(x + 1)
y - 4 = -x - 1
x + y = 3
(ii) For point A (on x-axis), y = 0.
Putting y = 0 in the equation of PQ, we get,
x = 3
Thus, the co-ordinates of point A are (3, 0).
For point B (on y-axis), x = 0.
Putting x = 0 in the equation of PQ, we get,
y = 3
Thus, the co-ordinates of point B are (0, 3).
(iii) M is the mid-point of AB.
So, the co-ordinates of point M are
![]()
(1, 5) and (-3, -1) are the co-ordinates of vertices A and C respectively of rhombus ABCD. Find the equations of the diagonals AC and BD.
A = (1, 5) and C = (-3, -1)
We know that in a rhombus, diagonals bisect each other at right angle.
Let O be the point of intersection of the diagonals AC and BD.
Co-ordinates of O are
![]()
Slope of AC = ![]()
For line AC:
Slope = m = ![]() , (x1, y1) = (1, 5)
, (x1, y1) = (1, 5)
Equation of the line AC is
y - y1 = m(x - x1)
y - 5 = ![]() (x - 1)
(x - 1)
2y - 10 = 3x - 3
3x - 2y + 7 = 0
For line BD:
Slope = m = ![]() , (x1, y1) = (-1, 2)
, (x1, y1) = (-1, 2)
Equation of the line BD is
y - y1 = m(x - x1)
y - 2 = ![]() (x + 1)
(x + 1)
3y - 6 = -2x - 2
2x + 3y = 4
Show that A (3, 2), B (6, -2) and C (2, -5) can be the vertices of a square.
(i) Find the co-ordinates of its fourth vertex D, if ABCD is a square.
(ii) Without using the co-ordinates of vertex D, find the equation of side AD of the square and also the equation of diagonal BD.

A line through origin meets the line x = 3y + 2 at right angles at point X. Find the co-ordinates of X.
The given line is
x = 3y + 2 ...(1)
3y = x - 2
![]()
Slope of this line is ![]() .
.
The required line intersects the given line at right angle.
![]() Slope of the required line =
Slope of the required line =
The required line passes through (0, 0) = (x1, y1)
The equation of the required line is
y - y1 = m(x - x1)
y - 0 = -3(x - 0)
3x + y = 0 ...(2)
Point X is the intersection of the lines (1) and (2).
Using (1) in (2), we get,
9y + 6 + y = 0
![]()
![]()
Thus, the co-ordinates of the point X are ![]() .
.
A straight line passes through the point (3, 2) and the portion of this line, intercepted between the positive axes, is bisected at this point. Find the equation of the line.
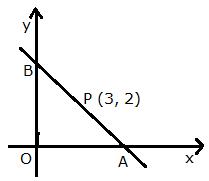
Let the line intersect the x-axis at point A (x, 0) and y-axis at point B (0, y).
Since, P is the mid-point of AB, we have:

Thus, A = (6, 0) and B = (0, 4)
Slope of line AB = ![]()
Let (x1, y1) = (6, 0)
The required equation of the line AB is given by
y - y1 = m(x - x1)
y - 0 = ![]() (x - 6)
(x - 6)
3y = -2x + 12
2x + 3y = 12
Find the equation of the line passing through the point of intersection of 7x + 6y = 71 and 5x - 8y = -23; and perpendicular to the line 4x - 2y = 1.
7x + 6y = 71 ![]() 28x + 24y = 284 ...(1)
28x + 24y = 284 ...(1)
5x - 8y = -23 ![]() 15x - 24y = -69 ...(2)
15x - 24y = -69 ...(2)
Adding (1) and (2), we get,
43x = 215
x = 5
From (2), 8y = 5x + 23 = 25 + 23 = 48 ![]() y = 6
y = 6
Thus, the required line passes through the point (5, 6).
4x - 2y = 1
2y = 4x - 1
y = 2x -![]()
Slope of this line = 2
Slope of the required line = ![]()
The required equation of the line is
y - y1 = m(x - x1)
y - 6 = ![]() (x - 5)
(x - 5)
2y - 12 = -x + 5
x + 2y = 17
Find the equation of the line which is perpendicular to the line ![]() at the point where this line meets y-axis.
at the point where this line meets y-axis.
The given line is
![]()
Slope of this line =![]()
Slope of the required line = 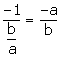
Let the required line passes through the point P (0, y).
Putting x = 0 in the equation ![]() , we get,
, we get,
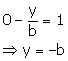
Thus, P = (0, -b) = (x1, y1)
The equation of the required line is
y - y1 = m(x - x1)
y + b = ![]() (x - 0)
(x - 0)
by + b2 = -ax
ax + by + b2 = 0
O (0, 0), A (3, 5) and B (-5, -3) are the vertices of triangle OAB. Find:
(i) the equation of median of triangle OAB through vertex O.
(ii) the equation of altitude of triangle OAB through vertex B.
(i) Let the median through O meets AB at D. So, D is the mid-point of AB.
Co-ordinates of point D are
![]()
Slope of OD = ![]()
(x1, y1) = (0, 0)
The equation of the median OD is
y - y1 = m(x - x1)
y - 0 = -1(x - 0)
x + y = 0
(ii) The altitude through vertex B is perpendicular to OA.
Slope of OA = ![]()
Slope of the required altitude = 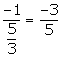
The equation of the required altitude through B is
y - y1 = m(x - x1)
y + 3 = ![]() (x + 5)
(x + 5)
5y + 15 = -3x - 15
3x + 5y + 30 = 0
Determine whether the line through points (-2, 3) and (4, 1) is perpendicular to the line 3x = y + 1.
Does the line 3x = y + 1 bisect the line segment joining the two given points?
Let A = (-2, 3) and B = (4, 1)
Slope of AB = m1 = ![]()
Equation of line AB is
y - y1 = m1(x - x1)
y - 3 = ![]() (x + 2)
(x + 2)
3y - 9 = -x - 2
x + 3y = 7 ...(1)
Slope of the given line 3x = y + 1 is 3 = m2.
![]()
Hence, the line through points A and B is perpendicular to the given line.
Given line is 3x = y +1 ...(2)
Solving (1) and (2), we get,
x = 1 and y = 2
So, the two lines intersect at point P = (1, 2).
The co-ordinates of the mid-point of AB are
![]()
Hence, the line 3x = y + 1 bisects the line segment joining the points A and B.
Given a straight line x cos ![]() + y sin
+ y sin ![]() = 2. Determine the equation of the other line which is parallel to it and passes through (4, 3).
= 2. Determine the equation of the other line which is parallel to it and passes through (4, 3).
x cos ![]() + y sin
+ y sin ![]() = 2
= 2
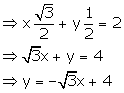
Slope of this line = ![]()
Slope of a line which is parallel to this given line = ![]()
Let (4, 3) = (x1, y1)
Thus, the equation of the required line is given by:
y - y1 = m1(x - x1)
y - 3 = ![]() (x - 4)
(x - 4)
![]()
Find the value of k such that the line (k - 2)x + (k + 3)y - 5 = 0 is:
(i) perpendicular to the line 2x - y + 7 = 0
(ii) parallel to it.
(k - 2)x + (k + 3)y - 5 = 0 ....(1)
(k + 3)y = -(k - 2)x + 5
y =![]()
Slope of this line = m1 = ![]()
(i) 2x - y + 7 = 0
y = 2x + 7 = 0
Slope of this line = m2 = 2
Line (1) is perpendicular to 2x - y + 7 = 0

(ii) Line (1) is parallel to 2x - y + 7 = 0
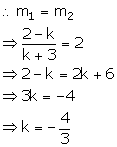
The vertices of a triangle ABC are A (0, 5), B (-1, -2) and C (11, 7). Write down the equation of BC. Find:
(i) the equation of line through A and perpendicular to BC.
(ii) the co-ordinates of the point, where the perpendicular through A, as obtained in (i), meets BC.
Slope of BC = ![]()
Equation of the line BC is given by
y - y1 = m1(x - x1)
y + 2 = ![]() (x + 1)
(x + 1)
4y + 8 = 3x + 3
3x - 4y = 5....(1)
(i) Slope of line perpendicular to BC = 
Required equation of the line through A (0, 5) and perpendicular to BC is
y - y1 = m1(x - x1)
y - 5 = ![]() (x - 0)
(x - 0)
3y - 15 = -4x
4x + 3y = 15 ....(2)
(ii) The required point will be the point of intersection of lines (1) and (2).
(1) ![]() 9x - 12y = 15
9x - 12y = 15
(2) ![]() 16x + 12y = 60
16x + 12y = 60
Adding the above two equations, we get,
25x = 75
x = 3
So, 4y = 3x - 5 = 9 - 5 = 4
y = 1
Thus, the co-ordinates of the required point is (3, 1).
From the given figure, find:
(i) the co-ordinates of A, B and C.
(ii) the equation of the line through A and parallel to BC.
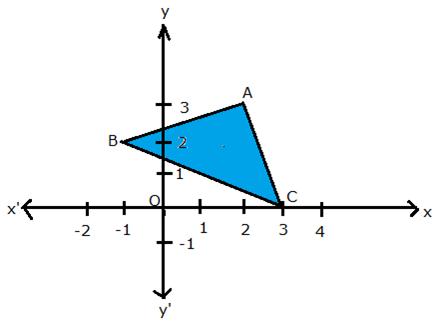
(i) A = (2, 3), B = (-1, 2), C = (3, 0)
(ii) Slope of BC = ![]()
Slope of required line which is parallel to BC = Slope of BC =![]()
(x1, y1) = (2, 3)
The required equation of the line through A and parallel to BC is given by:
y - y1 = m1(x - x1)
y - 3 = ![]() (x - 2)
(x - 2)
2y - 6 = -x + 2
x + 2y = 8
P (3, 4), Q (7, -2) and R (-2, -1) are the vertices of triangle PQR. Write down the equation of the median of the triangle through R.
The median (say RX) through R will bisect the line PQ.
The co-ordinates of point X are
![]()
Slope of RX =
(x1, y1) = (-2, -1)
The required equation of the median RX is given by:
y - y1 = m1(x - x1)
y + 1 = ![]() (x + 2)
(x + 2)
7y + 7 = 2x + 4
7y = 2x - 3
A (8, -6), B (-4, 2) and C (0, -10) are vertices of a triangle ABC. If P is the mid-point of AB and Q is the mid-point of AC, use co-ordinate geometry to show that PQ is parallel to BC. Give a special name of quadrilateral PBCQ.
P is the mid-point of AB. So, the co-ordinate of point P are
![]()
Q is the mid-point of AC. So, the co-ordinate of point Q are
![]()
Slope of PQ = ![]()
Slope of BC = ![]()
Since, slope of PQ = Slope of BC,
![]() PQ || BC
PQ || BC
Also, we have:
Slope of PB = ![]()
Slope of QC = ![]()
Thus, PB is not parallel to QC.
Hence, PBCQ is a trapezium.
A line AB meets the x-axis at point A and y-axis at point B. The point P (-4, -2) divides the line segment AB internally such that AP : PB = 1 : 2. Find:
(i) the co-ordinates of A and B.
(ii) the equation of line through P and perpendicular to AB.
(i) Let the co-ordinates of point A (lying on x-axis) be (x, 0) and the co-ordinates of point B (lying y-axis) be (0, y).
Given, P = (-4, -2) and AP: PB = 1:2
Using section formula, we have:
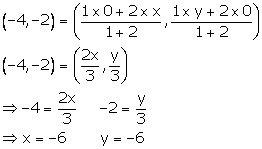
Thus, the co-ordinates of A and B are (-6, 0) and (0, -6).
(ii) Slope of AB = ![]()
Slope of the required line perpendicular to AB = ![]()
(x1, y1) = (-4, -2)
Required equation of the line passing through P and perpendicular to AB is given by
y - y1 = m(x - x1)
y + 2 = 1(x + 4)
y + 2 = x + 4
y = x + 2
A line intersects x-axis at point (-2, 0) and cuts off an intercept of 3 units from the positive side of y-axis. Find the equation of the line.
The required line intersects x-axis at point A (-2, 0).
Also, y-intercept = 3
So, the line also passes through B (0, 3).
Slope of line AB = ![]() = m
= m
(x1, y1) = (-2, 0)
Required equation of the line AB is given by
y - y1 = m(x - x1)
y - 0 = ![]() (x + 2)
(x + 2)
2y = 3x + 6
Find the equation of a line passing through the point (2, 3) and having the x-intercept of 4 units.
The required line passes through A (2, 3).
Also, x-intercept = 4
So, the required line passes through B (4, 0).
Slope of AB = ![]()
(x1, y1) = (4, 0)
Required equation of the line AB is given by
y - y1 = m(x - x1)
y - 0 = ![]() (x - 4)
(x - 4)
2y = -3x + 12
3x + 2y = 12
The given figure (not drawn to scale) shows two straight lines AB and CD. If equation of the line AB is: y = x + 1 and equation of line CD is: y = ![]() x - 1. Write down the inclination of lines AB and CD; also, find the angle
x - 1. Write down the inclination of lines AB and CD; also, find the angle ![]() between AB and CD.
between AB and CD.
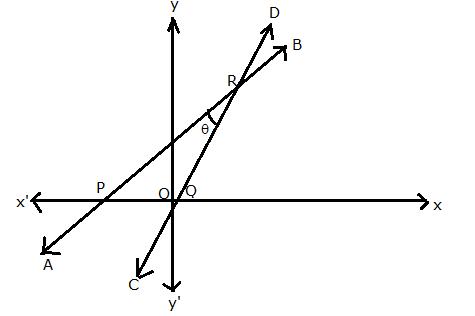
Equation of the line AB is y = x + 1
Slope of AB = 1
Inclination of line AB = ![]() (Since, tan 45o = 1)
(Since, tan 45o = 1)
![]()
Equation of line CD is y = ![]() x - 1
x - 1
Slope of CD = ![]()
Inclination of line CD = 60o (Since, tan 60o =![]() )
)
![]()
Using angle sum property in ![]() PQR,
PQR,
![]()
Write down the equation of the line whose gradient is ![]() and which passes through P, where P divides the line segment joining A (-2, 6) and B (3, -4) in the ratio 2: 3.
and which passes through P, where P divides the line segment joining A (-2, 6) and B (3, -4) in the ratio 2: 3.
Given, P divides the line segment joining A (-2, 6) and B (3, -4) in the ratio 2: 3.
Co-ordinates of point P are

Slope of the required line = m =![]()
The required equation of the line is given by
y - y1 = m(x - x1)
y - 2 = ![]() (x - 0)
(x - 0)
2y - 4 = 3x
2y = 3x + 4
The ordinate of a point lying on the line joining the points (6, 4) and (7, -5) is -23. Find the co-ordinates of that point.
Let A = (6, 4) and B = (7, -5)
Slope of the line AB = ![]()
(x1, y1) = (6, 4)
The equation of the line AB is given by
y - y1 = m(x - x1)
y - 4 = -9(x - 6)
y - 4 = -9x + 54
9x + y = 58 ...(1)
Now, given that the ordinate of the required point is -23.
Putting y = -23 in (1), we get,
9x - 23 = 58
9x = 81
x = 9
Thus, the co-ordinates of the required point is (9, -23).
Points A and B have coordinates (7, -3) and (1, 9) respectively. Find:
(i) the slope of AB.
(ii) the equation of the perpendicular bisector of the line segment AB.
(iii) the value of 'p' if (-2, p) lies on it.
Given points are A(7, -3) and B(1, 9).
(i) Slope of AB = ![]()
(ii) Slope of perpendicular bisector = ![]() =
= ![]()
Mid-point of AB = ![]() =(4, 3)
=(4, 3)
![]() Equation of perpendicular bisector is:
Equation of perpendicular bisector is:
y - 3 = ![]() (x - 4)
(x - 4)
2y - 6 = x - 4
x - 2y + 2 = 0
(iii) Point (-2, p) lies on x - 2y + 2 = 0.
![]() -2 - 2p + 2 = 0
-2 - 2p + 2 = 0
![]() 2p = 0
2p = 0
![]() p = 0
p = 0
A and B are two points on the x-axis and y-axis respectively. P (2, -3) is the mid-point of AB. Find the
(i) coordinates of A and B
(ii) slope of line AB
(iii) equation of line AB.
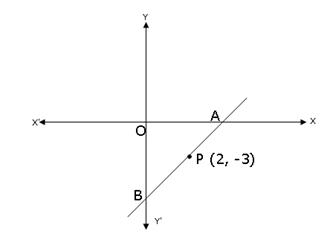
(i) Let the co-ordinates be A(x, 0) and B(0, y).
Mid-point of A and B is given by ![]()

(ii) Slope of line AB, m = ![]()
(iii) Equation of line AB, using A(4, 0)
![]()
2y = 3x - 12
The equation of a line 3x + 4y - 7 = 0. Find:
(i) the slope of the line.
(ii) the equation of a line perpendicular to the given line and passing through the intersection of the lines x - y + 2 = 0 and 3x + y - 10 = 0.
3x + 4y - 7 = 0 ...(1)
4y = -3x + 7
y = ![]()
(i) Slope of the line = m = ![]()
(ii) Slope of the line perpendicular to the given line = 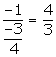
Solving the equations x - y + 2 = 0 and 3x + y - 10 = 0, we get x = 2 and y = 4.
So, the point of intersection of the two given lines is (2, 4).
Given that a line with slope ![]() passes through point (2, 4).
passes through point (2, 4).
Thus, the required equation of the line is
y - 4 = ![]() (x - 2)
(x - 2)
3y - 12 = 4x - 8
4x - 3y + 4 = 0
ABCD is a parallelogram where A(x, y), B(5, 8), C(4, 7) and D(2, -4). Find:
(i)Co-ordinates of A
(ii)Equation of diagonal BD
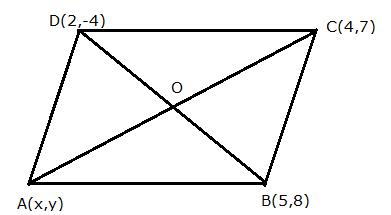
In parallelogram ABCD, A(x, y), B(5, 8), C(4, 7) and D(2, -4).
The diagonals of the parallelogram bisect each other.
O is the point of intersection of AC and BD
Since O is the midpoint of BD, its coordinates will be
![]()
(i)
Since O is the midpoint of AC also,
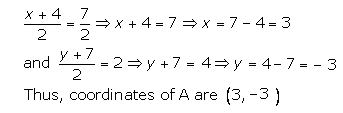
(ii)

Given equation of the line L1 is y = 4.
(i)Write the slope of the line L2 if L2 is the bisector of angle O
(ii)Write the coordinates of point P
(iii)Find the equation of L2
(i)
![]()
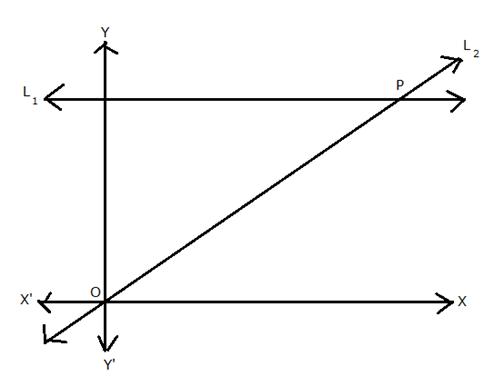
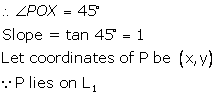
(ii)
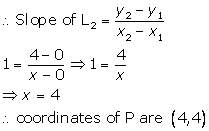
(iii)
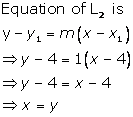
(i) equation of AB
(ii) equation of CD
Find the equation of the line that has x-intercept = -3 and is perpendicular to 3x + 5y = 1.
A straight line passes through the points P(-1, 4) and Q(5, -2). It intersects x-axis at point A and y-axis at point B. M is the mid point of the line segment AB. Find:
(i) the equation of the line.
(ii) the co-ordinates of points A and B.
(iii) the co-ordinates of point M

In the given figure. line AB meets y-axis at point A. Line through C(2, 10) and D intersects line AB at right angle at point R Find:
(i) equation of line AB
(ii) equation of line CD
(iii) co-ordinates of points E and D
A line through point P(4, 3) meets x-axis at point A and the y-axis at point B. If BP is double of PA, find the equation of AB.
Find the equation of line through the intersection of lines 2x - y = 1 and 3x + 2y = -9 and making an angle of 30° with positive direction of x-axis.
Find the equation of the line through the Points A(-1, 3) and B(0, 2). Hence, show that the points A, B and C(1, 1) are collinear.
Three vertices of a parallelogram ABCD taken in order are A(3, 6), B(5, 10) and C(3, 2), find :
(i) the co-ordinates of the fourth vertex D.
(ii) length of diagonal BD.
(iii) equation of side AB of the parallelogram ABCD.
In the figure, given, ABC is a triangle and BC is parallel to the y-axis. AB and AC intersect the y-axis at P and Q respectively.
(i) Write the co-ordinates of A.
(ii) Find the length of AB and AC.
(iii) Find the ratio in which Q divides AC.
(iv) Find the equation of the line AC.
![]()
i. k.
ii. mid-point of PQ, using the value of 'k' found in (i).
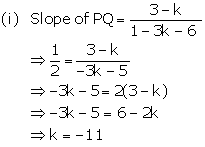
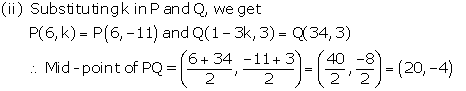
A line AB meets X-axis at A and Y-axis at B. P(4, -1) divides AB in the ration 1 : 2.
i. Find the co-ordinates of A and B.
ii. Find the equation of the line through P and perpendicular to AB.
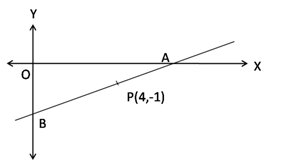
i. Since A lies on the X-axis, let the co-ordinates of A be (x, 0).
Since B lies on the Y-axis, let the co-ordinates of B be (0, y).
Let m = 1 and n = 2
Using Section formula,
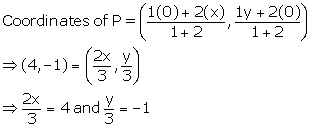
⇒ x = 6 and y = -3
So, the co-ordinates of A are (6, 0) and that of B are (0, -3).
![]()
⇒ Slope of line perpendicular to AB = m = -2
P = (4, -1)
Thus, the required equation is
y - y1 = m(x - x1)
⇒ y - (-1) = -2(x - 4)
⇒ y + 1 = -2x + 8
⇒ 2x + y = 7
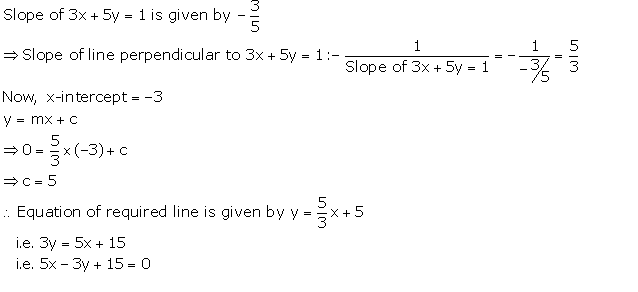


No comments:
Post a Comment