If a: b = 3: 5, find:
(10a + 3b): (5a + 2b)
Given, ![]()
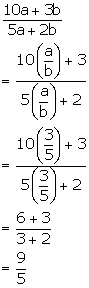
If 5x + 6y: 8x + 5y = 8: 9, find x: y.
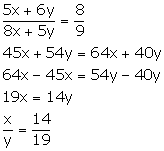
If (3x - 4y): (2x - 3y) = (5x - 6y): (4x - 5y), find x: y.
(3x - 4y): (2x - 3y) = (5x - 6y): (4x - 5y)

Find the:
(i) duplicate ratio of ![]()
(ii) triplicate ratio of 2a: 3b
(iii) sub-duplicate ratio of 9x2a4 : 25y6b2
(iv) sub-triplicate ratio of 216: 343
(v) reciprocal ratio of 3: 5
(vi) ratio compounded of the duplicate ratio of 5: 6, the reciprocal ratio of 25: 42 and the sub-duplicate ratio of 36: 49.
(i) Duplicate ratio of ![]()
(ii) Triplicate ratio of 2a: 3b = (2a)3: (3b)3 = 8a3 : 27b3
(iii) Sub-duplicate ratio of 9x2a4 : 25y6b2 = ![]()
(iv) Sub-triplicate ratio of 216: 343 = ![]()
(v) Reciprocal ratio of 3: 5 = 5: 3
(vi) Duplicate ratio of 5: 6 = 25: 36
Reciprocal ratio of 25: 42 = 42: 25
Sub-duplicate ratio of 36: 49 = 6: 7
Required compound ratio = ![]()
Find the value of x, if:
(i) (2x + 3): (5x - 38) is the duplicate ratio of ![]()
(ii) (2x + 1): (3x + 13) is the sub-duplicate ratio of 9: 25.
(iii) (3x - 7): (4x + 3) is the sub-triplicate ratio of 8: 27.
(i) (2x + 3): (5x - 38) is the duplicate ratio of ![]()
Duplicate ratio of ![]()
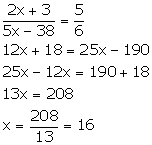
(ii) (2x + 1): (3x + 13) is the sub-duplicate ratio of 9: 25
Sub-duplicate ratio of 9: 25 = 3: 5

(iii) (3x - 7): (4x + 3) is the sub-triplicate ratio of 8: 27
Sub-triplicate ratio of 8: 27 = 2: 3
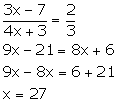
What quantity must be added to each term of the ratio x: y so that it may become equal to c: d?
Let the required quantity which is to be added be p.
Then, we have:
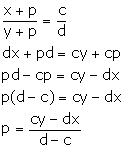
A woman reduces her weight in the ratio 7 : 5. What does her weight become if originally it was 84 kg?
If 15(2x2 - y2) = 7xy, find x: y; if x and y both are positive.
15(2x2 - y2) = 7xy

Find the:
(i) fourth proportional to 2xy, x2 and y2.
(ii) third proportional to a2 - b2 and a + b.
(iii) mean proportional to (x - y) and (x3 - x2y).
(i) Let the fourth proportional to 2xy, x2 and y2 be n.
![]() 2xy: x2 = y2: n
2xy: x2 = y2: n
![]() 2xy
2xy ![]() n = x2
n = x2![]() y2
y2
![]() n =
n =![]()
(ii) Let the third proportional to a2 - b2 and a + b be n.
![]() a2 - b2, a + b and n are in continued proportion.
a2 - b2, a + b and n are in continued proportion.
![]() a2 - b2 : a + b = a + b : n
a2 - b2 : a + b = a + b : n
![]() n =
n =![]()
(iii) Let the mean proportional to (x - y) and (x3 - x2y) be n.
![]() (x - y), n, (x3 - x2y) are in continued proportion
(x - y), n, (x3 - x2y) are in continued proportion
![]() (x - y) : n = n : (x3 - x2y)
(x - y) : n = n : (x3 - x2y)
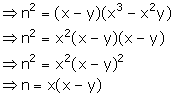
Find two numbers such that the mean proportional between them is 14 and third proportional to them is 112.
Let the required numbers be a and b.
Given, 14 is the mean proportional between a and b.
![]() a: 14 = 14: b
a: 14 = 14: b
![]() ab = 196
ab = 196
![]()
Also, given, third proportional to a and b is 112.
![]() a: b = b: 112
a: b = b: 112
![]()
Using (1), we have:
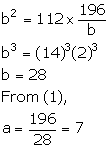
Thus, the two numbers are 7 and 28.
If x and y be unequal and x: y is the duplicate ratio of x + z and y + z, prove that z is mean proportional between x and y.
Given, ![]()
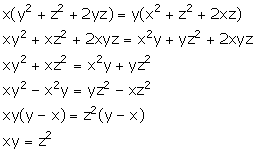
Hence, z is mean proportional between x and y.
If ![]() , find the value of
, find the value of ![]() .
.

If (4a + 9b) (4c - 9d) = (4a - 9b) (4c + 9d), prove that:
a: b = c: d.
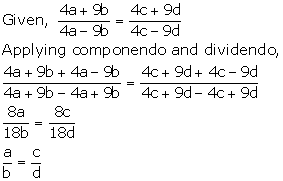
If ![]() , show that:
, show that:
(a + b) : (c + d) = ![]()
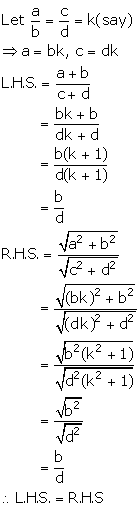
There are 36 members in a student council in a school and the ratio of the number of boys to the number of girls is 3: 1. How any more girls should be added to the council so that the ratio of the number of boys to the number of girls may be 9: 5?
Ratio of number of boys to the number of girls = 3: 1
Let the number of boys be 3x and number of girls be x.
![]() 3x + x = 36
3x + x = 36
4x = 36
x = 9
![]() Number of boys = 27
Number of boys = 27
Number of girls = 9
Le n number of girls be added to the council.
From given information, we have:
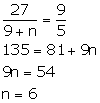
Thus, 6 girls are added to the council.
If 7x - 15y = 4x + y, find the value of x: y. Hence, use componendo and dividend to find the values of:
7x - 15y = 4x + y
7x - 4x = y + 15y
3x = 16y
![]()

If ![]() , use properties of proportion to find:
, use properties of proportion to find:
(i) m: n
(ii) ![]()
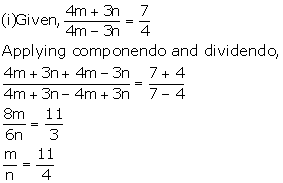

If x, y, z are in continued proportion, prove that 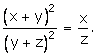
![]() x, y, z are in continued proportion,
x, y, z are in continued proportion,
![]()
![]()
Therefore,
![]()
![]()
![]() (By alternendo)
(By alternendo)
![]()
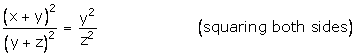
![]()

![]()

Hence Proved.
Given x =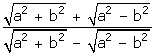 .
.
Use componendo and dividendo to prove that b2 =![]() .
.
x = 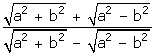
By componendo and dividendo,

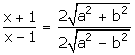
Squaring both sides,
![]()
By componendo and dividendo,
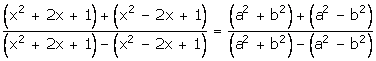
![]()
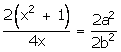
![]()
![]()
![]() b2 =
b2 = ![]()
Hence Proved.
If ![]() , find:
, find:
![]()

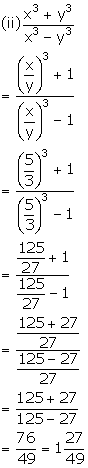
Using componendo and dividendo find the value of x:
![]()



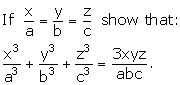
![]()

If b is the mean proportion between a and c, show that:
![]()
Given that b is the mean proportion between a and c.
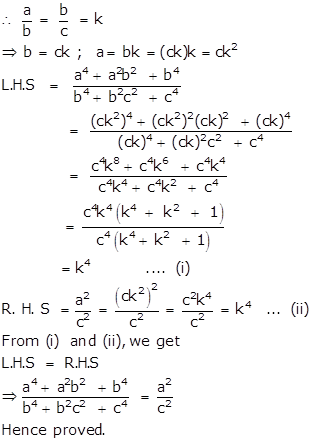
If ![]() , use properties of proportion to find:
, use properties of proportion to find:
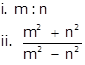
i.
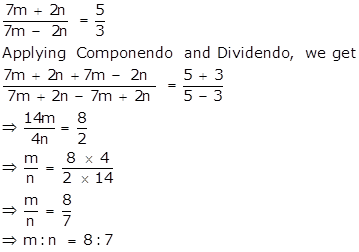
ii.
From (i),
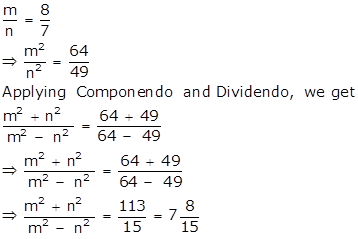
i. If x and y both are positive and (2x2 - 5y2): xy = 1: 3, find x: y.
ii. Find x, if![]() .
.
i. (2x2 - 5y2): xy = 1: 3
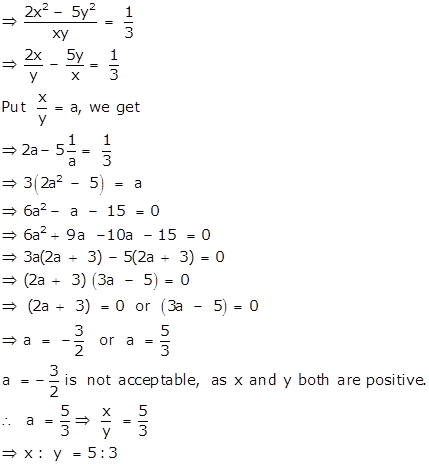
ii.
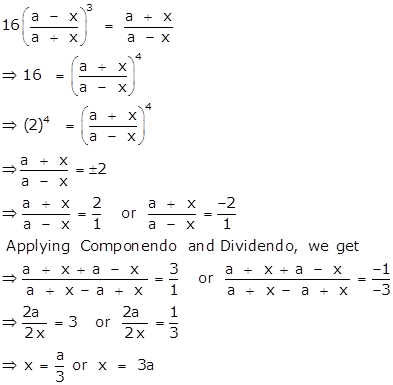
No comments:
Post a Comment