Chapter 10 - Arithmetic Progression Exercise Ex. 10(D)

Question 1

Find three numbers in A.P. whose sum is 24 and whose product is 440.

Solution 1

Question 2

The sum of three consecutive terms of an A.P. is 21 and the sum of their squares is 165. Find these terms

Solution 2

Question 3

The angles of a quadrilateral are in A.P. with common difference 20^o. Find its angles.

Solution 3

Question 4

Divide 96 into four parts which are in A.P and the ratio between product of their means to product of their extremes is 15 :7.

Solution 4

 

Question 5

Find five numbers in A.P. whose sum is 12.5 and the ratio of the first to the last terms is 2: 3.

Solution 5

We know that,

Sum of n terms of an A.P = 

Let the first term be 2x and the last term be 3x.

 ∴ Sum of 5 terms of an A.P =  

 

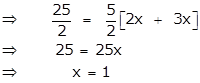
First term = 2x =2 × 1 = 2 and the last term = 3x = 3 × 1 = 3

n^th term of an A.P. is given by

t_n = a + (n - 1)d

⇒ a₅ = 2 + (5 - 1)d

⇒ 3 = 2 + 4d

⇒ 1 = 4d

⇒ d =  = 0.25

Therefore the five numbers in an A.P are 2, 2.25, 2.50, 2.75 and 3.

 

 

 

Question 6

Split 207 into three parts such that these parts are in A.P. and the product of the two smaller parts is 4623.

Solution 6

Question 7

The sum of three numbers in A.P. is 15 and the sum of the squares of the extreme terms is 58. Find the numbers.

Solution 7

Question 8

Find four numbers in A.P. whose sum is 20 and the sum of whose squares is 120.

Solution 8

 

Question 9

Insert one arithmetic mean between 3 and 13

Solution 9

Question 10

The angles of a polygon are in A.P with common difference 5^o. If the smallest angle is 120^o, find the number of sides of the polygon

 

Let the number sides be n

 

Solution 10

Question 11

Solution 11