(i) The ratio between the corresponding sides of two similar triangles is 2 is to 5. Find the ratio between the areas of these triangles.
(ii) Areas of two similar triangles are 98 sq. cm and 128 sq. cm. Find the ratio between the lengths of their corresponding sides.
We know that the ratio of the areas of two similar triangles is equal to the ratio of squares of their corresponding sides.
(i) Required ratio = ![]()
(ii) Required ratio = ![]()
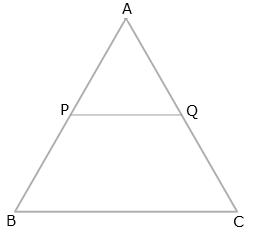
A line PQ is drawn parallel to the base BC of ![]() ABC which meets sides AB and AC at points P and Q respectively. If AP =
ABC which meets sides AB and AC at points P and Q respectively. If AP =![]() PB; find the value of:
PB; find the value of:
(i) ![]()
(ii) ![]()
(i) AP =![]() PB
PB ![]()

(ii) 
The perimeters of two similar triangles are 30 cm and 24 cm. If one side of the first triangle is 12 cm, determine the corresponding side of the second triangle.
Let ![]()

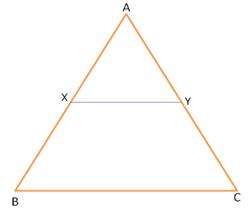
In the given figure, AX: XB = 3: 5.
Find:
(i) the length of BC, if the length of XY is 18 cm.
(ii) the ratio between the areas of trapezium XBCY and triangle ABC.
Given, ![]()
(i)

(ii)
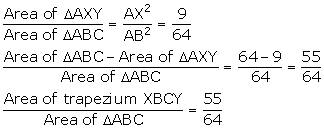
ABC is a triangle. PQ is a line segment intersecting AB in P and AC in Q such that PQ || BC and divides triangle ABC into two parts equal in area. Find the value of ratio BP: AB.

From the given information, we have:
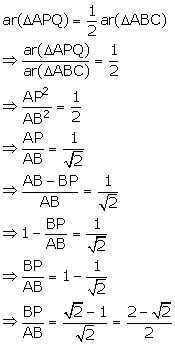
In the given triangle PQR, LM is parallel to QR and PM: MR = 3: 4.
Calculate the value of ratio:
(i) ![]()
(ii) ![]()
(iii) ![]()

(i)

(ii) Since ![]() LMN and
LMN and ![]() MNR have common vertex at M and their bases LN and NR are along the same straight line
MNR have common vertex at M and their bases LN and NR are along the same straight line

(iii) Since ![]() LQM and
LQM and ![]() LQN have common vertex at L and their bases QM and QN are along the same straight line
LQN have common vertex at L and their bases QM and QN are along the same straight line
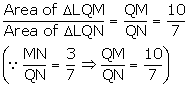
The given diagram shows two isosceles triangles which are similar also. In the given diagram, PQ and BC are not parallel; PC = 4, AQ = 3, QB = 12, BC = 15 and AP = PQ. Calculate:
(i) the length of AP,
(ii) the ratio of the areas of triangle APQ and triangle ABC.
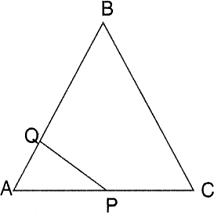
(i)

(ii)
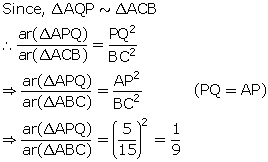
In the figure, given below, ABCD is a parallelogram. P is a point on BC such that BP: PC = 1: 2. DP produced meets AB produces at Q. Given the area of triangle CPQ = 20 cm2. Calculate:
(i) area of triangle CDP,
(ii) area of parallelogram ABCD.


In the given figure, BC is parallel to DE. Area of triangle ABC = 25 cm2, Area of trapezium BCED = 24 cm2 and DE = 14 cm. Calculate the length of BC. Also, find the area of triangle BCD.

The given figure shows a trapezium in which AB is parallel to DC and diagonals AC and BD intersects at point P. If AP: CP = 3: 5, find:
(i) ![]() APB :
APB : ![]() CPB(ii)
CPB(ii) ![]() DPC :
DPC : ![]() APB
APB
(iii) ![]() ADP :
ADP : ![]() APB(iv)
APB(iv) ![]() APB :
APB : ![]() ADB
ADB
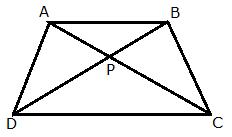
(i) Since ![]() APB and
APB and ![]() CPB have common vertex at B and their bases AP and PC are along the same straight line
CPB have common vertex at B and their bases AP and PC are along the same straight line
![]()
(ii) Since ![]() DPC and
DPC and ![]() BPA are similar
BPA are similar
![]()
(iii) Since ![]() ADP and
ADP and ![]() APB have common vertex at A and their bases DP and PB are along the same straight line
APB have common vertex at A and their bases DP and PB are along the same straight line

(iv) Since ![]() APB and
APB and ![]() ADB have common vertex at A and their bases BP and BD are along the same straight line
ADB have common vertex at A and their bases BP and BD are along the same straight line

In the given figure, ABC is a triangle. DE is parallel to BC and ![]() .
.

(i) Determine the ratios ![]()
(ii) Prove that ![]() DEF is similar to
DEF is similar to ![]() CBF. Hence, find
CBF. Hence, find ![]() .
.
(iii) What is the ratio of the areas of ![]() DEF and
DEF and ![]() BFC?
BFC?

(i) Given, DE || BC and ![]()
In ![]() ADE and
ADE and ![]() ABC,
ABC,
![]() A =
A = ![]() A(Corresponding Angles)
A(Corresponding Angles)
![]() ADE =
ADE = ![]() ABC(Corresponding Angles)
ABC(Corresponding Angles)
![]()
![]() (By AA- similarity)
(By AA- similarity)
![]()
![]() ..........(1)
..........(1)
Now![]()
Using (1), we get![]() .........(2)
.........(2)
(ii) In ![]() DEF and
DEF and ![]() CBF,
CBF,
![]() FDE =
FDE = ![]() FCB(Alternate Angle)
FCB(Alternate Angle)
![]() DFE =
DFE = ![]() BFC(Vertically Opposite Angle)
BFC(Vertically Opposite Angle)
![]()
![]() DEF
DEF ![]()
![]() CBF(By AA- similarity)
CBF(By AA- similarity)
![]() using (2)
using (2)
![]() .
.
(iii) Since the ratio of the areas of two similar triangles is equal to the square of the ratio of their corresponding sides, therefore
![]()
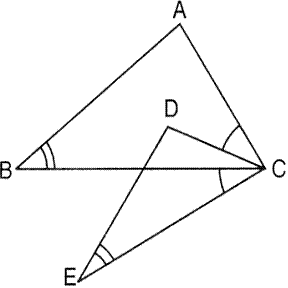
In the given figure, ![]() B =
B = ![]() E,
E, ![]() ACD =
ACD = ![]() BCE, AB = 10.4 cm and DE = 7.8 cm. Find the ratio between areas of the
BCE, AB = 10.4 cm and DE = 7.8 cm. Find the ratio between areas of the ![]() ABC and
ABC and ![]() DEC.
DEC.
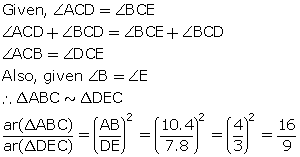
No comments:
Post a Comment