In the figure, given below, straight lines AB and CD intersect at P; and AC ‖ BD. Prove that :
If BD = 2.4 cm, AC = 3.6 cm, PD = 4.0 cm and PB = 3.2 cm; find the lengths of PA and PC.
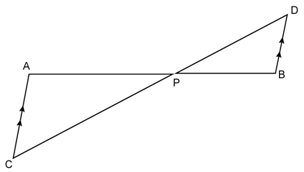

In the figure, given below, straight lines AB and CD intersect at P; and AC ‖ BD. Prove that:
ΔAPC and ΔBPD are similar.
In a trapezium ABCD, side AB is parallel to side DC; and the diagonals AC and BD intersect each other at point P. Prove that :
Δ APB is similar to Δ CPD.
In a trapezium ABCD, side AB is parallel to side DC; and the diagonals AC and BD intersect each other at point P. Prove that :
PA x PD = PB x PC.
P is a point on side BC of a parallelogram ABCD. If DP produced meets AB produced at point L, prove that :
DP : PL = DC : BL.
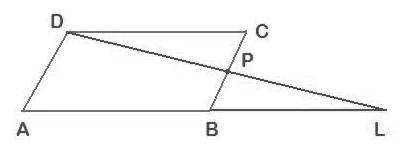

P is a point on side BC of a parallelogram ABCD. If DP produced meets AB produced at point L, prove that :
DL : DP = AL : DC.
In quadrilateral ABCD, the diagonals AC and BD intersect each other at point O. If AO = 2CO and BO = 2DO; show that :
Δ AOB is similar to Δ COD.
In quadrilateral ABCD, the diagonals AC and BD intersect each other at point O. If AO = 2CO and BO = 2DO; show that :
OA x OD = OB x OC.
In Δ ABC, angle ABC is equal to twice the angle ACB, and bisector of angle ABC meets the opposite side at point P. Show that :
CB : BA = CP : PA
In Δ ABC, angle ABC is equal to twice the angle ACB, and bisector of angle ABC meets the opposite side at point P. Show that :
AB x BC = BP x CA
In the given figure, DE ‖ BC, AE = 15 cm, EC = 9 cm, NC = 6 cm and BN = 24 cm.
Write all possible pairs of similar triangles.
In the given figure, DE ‖ BC, AE = 15 cm, EC = 9 cm, NC = 6 cm and BN = 24 cm.
Find lengths of ME and DM.
In the given figure, AD = AE and AD2 = BD x EC.
Prove that: triangles ABD and CAE are similar.
In the given figure, AB ‖ DC, BO = 6 cm and DQ = 8 cm; find: BP x DO.
Angle BAC of triangle ABC is obtuse and AB = AC. P is a point in BC such that PC = 12 cm. PQ and PR are perpendiculars to sides AB and AC respectively. If PQ = 15 cm and PR = 9 cm; find the length of PB.
State, true or false:
(i) Two similar polygons are necessarily congruent.
(ii) Two congruent polygons are necessarily similar.
(iii) All equiangular triangles are similar.
(iv) All isosceles triangles are similar.
(v) Two isosceles-right triangles are similar.
(vi) Two isosceles triangles are similar, if an angle of one is congruent to the corresponding angle of the other.
(vii) The diagonals of a trapezium, divide each other into proportional segments.
(i) False
(ii) True
(iii) True
(iv) False
(v) True
(vi) True
(vii) True
Given: ![]() GHE =
GHE = ![]() DFE = 90o, DH = 8, DF = 12, DG = 3x - 1 and DE = 4x + 2.
DFE = 90o, DH = 8, DF = 12, DG = 3x - 1 and DE = 4x + 2.
Find: the lengths of segments DG and DE.

D is a point on the side BC of triangle ABC such that angle ADC is equal to angle BAC. Prove that: CA2 = CB ![]() CD.
CD.
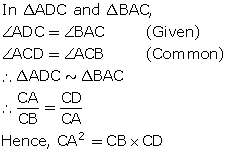
In the given figure, ∆ABC and ∆AMP are right angled at B and M respectively.
Given AC = 10 cm, AP = 15 cm and PM = 12 cm.
- ∆ ABC ~ ∆ AMP.
- Find AB and BC.

(i) In ∆ ABC and ∆ AMP,
![]() BAC=
BAC= ![]() PAM [Common]
PAM [Common]
![]() ABC=
ABC= ![]() PMA [Each = 90°]
PMA [Each = 90°]
∆ ABC ~ ∆ AMP [AA Similarity]
(ii)
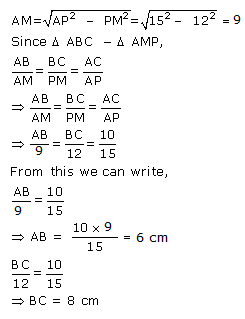
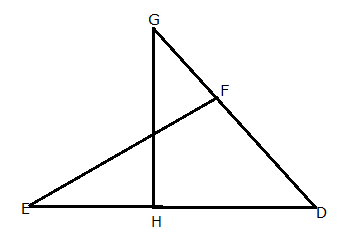
Given: RS and PT are altitudes of ![]() PQR. Prove that:
PQR. Prove that:
(i) ![]()
(ii) PQ ![]() QS = RQ
QS = RQ ![]() QT.
QT.
(i)
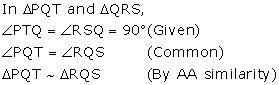
(ii)
Since, triangles PQT and RQS are similar.
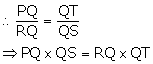
Given: ABCD is a rhombus, DPR and CBR are straight lines. Prove that: DP ![]() CR = DC
CR = DC ![]() PR.
PR.

Hence, DP ![]() CR = DC
CR = DC ![]() PR
PR
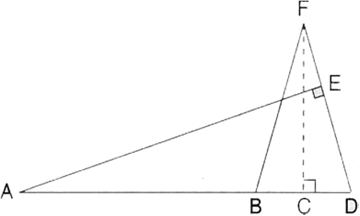
Given: FB = FD, AE ![]() FD and FC
FD and FC ![]() AD. Prove:
AD. Prove: ![]()

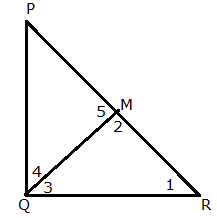
In ![]() PQR,
PQR, ![]() Q = 90o and QM is perpendicular to PR. Prove that:
Q = 90o and QM is perpendicular to PR. Prove that:
(i) PQ2 = PM ![]() PR
PR
(ii) QR2 = PR ![]() MR
MR
(iii) PQ2 + QR2 = PR2
(i) In ![]() PQM and
PQM and ![]() PQR,
PQR,
![]() PMQ =
PMQ = ![]() PQR = 90o
PQR = 90o
![]() QPM =
QPM = ![]() RPQ (Common)
RPQ (Common)
![]()
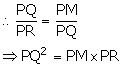
(ii) In ![]() QMR and
QMR and ![]() PQR,
PQR,
![]() QMR =
QMR = ![]() PQR = 90o
PQR = 90o
![]() QRM =
QRM = ![]() QRP (Common)
QRP (Common)
![]()
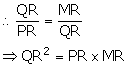
(iii) Adding the relations obtained in (i) and (ii), we get,
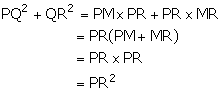
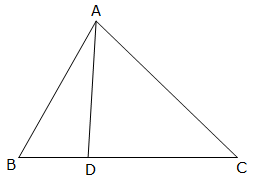
In ![]() ABC,
ABC, ![]() B = 90o and BD
B = 90o and BD ![]() AC.
AC.
(i) If CD = 10 cm and BD = 8 cm; find AD.
(ii) If AC = 18 cm and AD = 6 cm; find BD.
(iii) If AC = 9 cm and AB = 7 cm; find AD.

(i) In ![]() CDB,
CDB,
![]() 1 +
1 + ![]() 2 +
2 +![]() 3 = 180o
3 = 180o
![]() 1 +
1 + ![]() 3 = 90o ..... (1)(Since,
3 = 90o ..... (1)(Since, ![]() 2 = 90o)
2 = 90o)
![]() 3 +
3 + ![]() 4 = 90o .....(2) (Since,
4 = 90o .....(2) (Since, ![]() ABC = 90o)
ABC = 90o)
From (1) and (2),
![]() 1 +
1 + ![]() 3 =
3 = ![]() 3 +
3 + ![]() 4
4
![]() 1 =
1 = ![]() 4
4
Also, ![]() 2 =
2 = ![]() 5 = 90o
5 = 90o

Hence, AD = 6.4 cm

(iii)
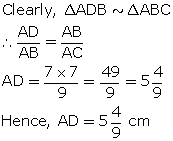
In the figure, PQRS is a parallelogram with PQ = 16 cm and QR = 10 cm. L is a point on PR such that RL: LP = 2: 3. QL produced meets RS at M and PS produced at N.
Find the lengths of PN and RM.
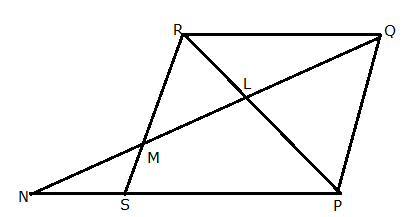

In quadrilateral ABCD, diagonals AC and BD intersect at point E such that AE: EC = BE: ED. Show that ABCD is a trapezium.
Given, AE: EC = BE: ED
Draw EF || AB
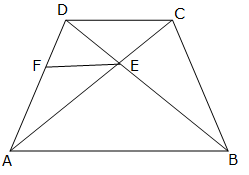
In ![]() ABD, EF || AB
ABD, EF || AB
Using Basic Proportionality theorem,

Thus, in ![]() DCA, E and F are points on CA and DA respectively such that
DCA, E and F are points on CA and DA respectively such that ![]()
Thus, by converse of Basic proportionality theorem, FE || DC.
But, FE || AB.
Hence, AB || DC.
Thus, ABCD is a trapezium.
In triangle ABC, AD is perpendicular to side BC and AD2 = BD ![]() DC. Show that angle BAC = 90o.
DC. Show that angle BAC = 90o.
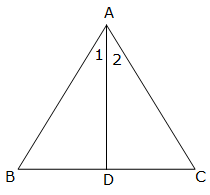
Given, AD2 = BD ![]() DC
DC
![]()
![]()
So, these two triangles will be equiangular.

In the given figure, AB || EF || DC; AB = 67.5 cm, DC = 40.5 cm and AE = 52.5 cm.
(i) Name the three pairs of similar triangles.
(ii) Find the lengths of EC and EF.
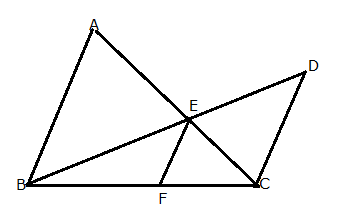
(i) The three pair of similar triangles are:
![]() BEF and
BEF and ![]() BDC
BDC
![]() CEF and
CEF and ![]() CAB
CAB
![]() ABE and
ABE and ![]() CDE
CDE
(ii) Since, ![]() ABE and
ABE and ![]() CDE are similar,
CDE are similar,

Since, ![]() CEF and
CEF and ![]() CAB are similar,
CAB are similar,

In the given figure, QR is parallel to AB and DR is parallel to QB. Prove that: PQ2 = PD ![]() PA.
PA.
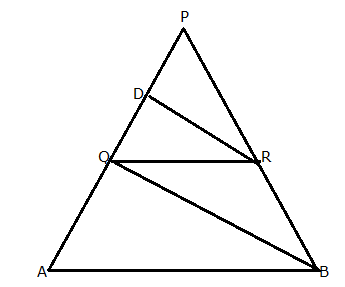
Given, QR is parallel to AB. Using Basic proportionality theorem,
![]()
Also, DR is parallel to QB. Using Basic proportionality theorem,
![]()
From (1) and (2), we get,

Through the mid-point M of the side CD of a parallelogram ABCD, the line BM is drawn intersecting diagonal AC in L and AD produced in E. Prove that: EL = 2BL.
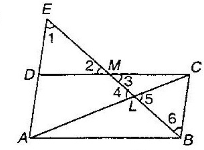
![]() 1 =
1 = ![]() 6 (Alternate interior angles)
6 (Alternate interior angles)
![]() 2 =
2 = ![]() 3 (Vertically opposite angles)
3 (Vertically opposite angles)
DM = MC (M is the mid-point of CD)
![]()
So, DE = BC (Corresponding parts of congruent triangles)
Also, AD = BC (Opposite sides of a parallelogram)
![]() AE = AD + DE = 2BC
AE = AD + DE = 2BC
Now, ![]() 1 =
1 = ![]() 6 and
6 and ![]() 4 =
4 = ![]() 5
5
![]()

In the figure, given below, P is a point on AB such that AP: PB = 4: 3. PQ is parallel to AC.
(i) Calculate the ratio PQ: AC, giving reason for your answer.
(ii) In triangle ARC, ![]() ARC = 90o and in triangle PQS,
ARC = 90o and in triangle PQS, ![]() PSQ = 90o. Given QS = 6 cm, calculate the length of AR.
PSQ = 90o. Given QS = 6 cm, calculate the length of AR.
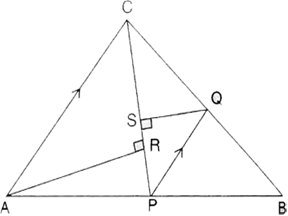
(i) Given, AP: PB = 4: 3.
Since, PQ || AC. Using Basic Proportionality theorem,

Now, ![]() PQB =
PQB = ![]() ACB (Corresponding angles)
ACB (Corresponding angles)
![]() QPB =
QPB = ![]() CAB (Corresponding angles)
CAB (Corresponding angles)
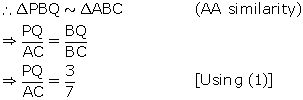
(ii) ![]() ARC =
ARC = ![]() QSP = 90o
QSP = 90o
![]() ACR =
ACR = ![]() SPQ (Alternate angles)
SPQ (Alternate angles)

In the right-angled triangle QPR, PM is an altitude. Given that QR = 8 cm and MQ = 3.5 cm, calculate the value of PR.
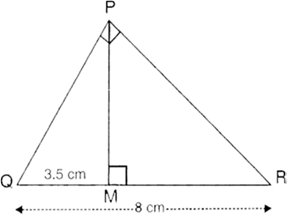
We have:

In the figure, given below, the medians BD and CE of a triangle ABC meet at G. Prove that:
(i) ![]() and
and
(ii) BG = 2 GD from (i) above.
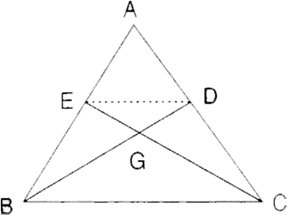
(i) Since, BD and CE are medians.
AD = DC
AE = BE
Hence, by converse of Basic Proportionality theorem,
ED || BC
In ![]() EGD and
EGD and ![]() CGB,
CGB,

(ii) Since, ![]()
![]()
In ![]() AED and
AED and ![]() ABC,
ABC,

From (1),

No comments:
Post a Comment