In the following figure, XY is parallel to BC, AX = 9 cm, XB = 4.5 cm and BC = 18 cm.
In the following figure, XY is parallel to BC, AX = 9 cm, XB = 4.5 cm and BC = 18 cm.
In the following figure, ABCD to a trapezium with AB ‖ DC. If AB = 9 cm, DC = 18 cm, CF= 13.5,cm, AP = 6 cm and BE = 15 cm, Calculate: PE


In the following figure, ABCD to a trapezium with AB ‖ DC. If AB = 9 cm, DC = 18 cm, CF= 13.5,cm, AP = 6 cm and BE = 15 cm, Calculate: CE
In the following figure, ABCD to a trapezium with AB ‖ DC. If AB = 9 cm, DC = 18 cm, CF= 13.5,cm, AP = 6 cm and BE = 15 cm, Calculate: AF
In the following figure, AB, CD and EF are perpendicular to the straight line BDF.
Triangle ABC is similar to triangle PQR. If AD and PM are corresponding medians of the two triangles, prove that: .
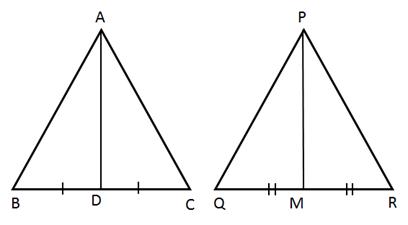

Triangle ABC is similar to triangle PQR. If bisector of angle BAC meets BC at point D and bisector of angle QPR meets QR at point M, prove that:.

In the following figure, ∠AXY = ∠AYX. If show that triangle ABC is isosceles.

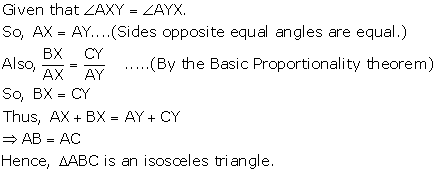
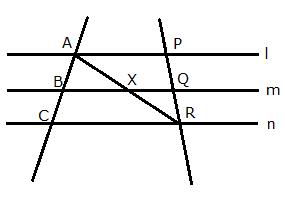
In the following diagram, lines l, m and n are parallel to each other. Two transversals p and q intersect the parallel lines at points A, B, C and P, Q, R as shown.
Prove that: ![]()

Join AR.
In ![]() ACR, BX || CR. By Basic Proportionality theorem,
ACR, BX || CR. By Basic Proportionality theorem,
![]()
In ![]() APR, XQ || AP. By Basic Proportionality theorem,
APR, XQ || AP. By Basic Proportionality theorem,
![]()
From (1) and (2), we get,
![]()
In the figure given below, AB ‖ EF ‖ CD. If AB = 22.5 cm, EP = 7.5 cm, PC = 15 cm and DC = 27 cm. Calculate : EF
In the figure given below, AB ‖ EF ‖ CD. If AB = 22.5 cm, EP = 7.5 cm, PC = 15 cm and DC = 27 cm. Calculate : AC
In ΔABC, ∠ABC = ∠DAC, AB = 8 cm, AC = 4 cm and AD = 5 cm.
Prove that ΔACD is similar to ΔBCA.
In ΔABC, ∠ABC = ∠DAC, AB = 8 cm, AC = 4 cm and AD = 5 cm.
Find BC and CD.

In ΔABC, ∠ABC = ∠DAC, AB = 8 cm, AC = 4 cm and AD = 5 cm.
Find area of ΔACD : area of ΔABC.
In the given triangle P, Q and R are mid-points of sides AB, BC and AC respectively. Prove that triangle QRP is similar to triangle ABC.
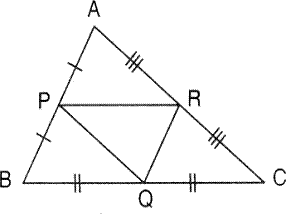
In ![]() ABC, PR || BC. By Basic proportionality theorem,
ABC, PR || BC. By Basic proportionality theorem,
![]()
Also, in ![]() PAR and
PAR and ![]() ABC,
ABC,

Similarly, ![]()
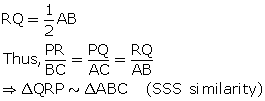
In the following figure, AD and CE are medians of ![]() ABC. DF is drawn parallel to CE. Prove that:
ABC. DF is drawn parallel to CE. Prove that:
(i) EF = FB,
(ii) AG: GD = 2: 1
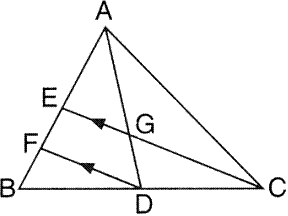
(i)

(ii) In ![]() AFD, EG || FD. Using Basic Proportionality theorem,
AFD, EG || FD. Using Basic Proportionality theorem,
![]() … (1)
… (1)
Now, AE = EB (as E is the mid-point of AB)
AE = 2EF (Since, EF = FB, by (i))
From (1),
![]()
Hence, AG: GD = 2: 1.
Two similar triangles are equal in area. Prove that the triangles are congruent.
Let us assume two similar triangles as ![]() ABC
ABC ![]()
![]() PQR
PQR

The ratio between the altitudes of two similar triangles is 3: 5; write the ratio between their:
(i) medians. (ii) perimeters. (iii) areas.
The ratio between the altitudes of two similar triangles is same as the ratio between their sides.
(i) The ratio between the medians of two similar triangles is same as the ratio between their sides.
![]() Required ratio = 3: 5
Required ratio = 3: 5
(ii) The ratio between the perimeters of two similar triangles is same as the ratio between their sides.
![]() Required ratio = 3: 5
Required ratio = 3: 5
(iii) The ratio between the areas of two similar triangles is same as the square of the ratio between their corresponding sides.
![]() Required ratio = (3)2 : (5)2 = 9: 25
Required ratio = (3)2 : (5)2 = 9: 25
The ratio between the areas of two similar triangles is 16: 25. Find the ratio between their:
(i) perimeters. (ii) altitudes. (iii) medians.
The ratio between the areas of two similar triangles is same as the square of the ratio between their corresponding sides.
So, the ratio between the sides of the two triangles = 4: 5
(i) The ratio between the perimeters of two similar triangles is same as the ratio between their sides.
![]() Required ratio = 4: 5
Required ratio = 4: 5
(ii) The ratio between the altitudes of two similar triangles is same as the ratio between their sides.
![]() Required ratio = 4: 5
Required ratio = 4: 5
(iii) The ratio between the medians of two similar triangles is same as the ratio between their sides.
![]() Required ratio = 4: 5
Required ratio = 4: 5
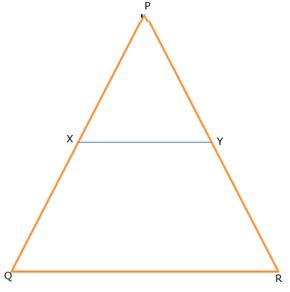
The following figure shows a triangle PQR in which XY is parallel to QR. If PX: XQ = 1: 3 and QR = 9 cm, find the length of XY.
Further, if the area of ![]() PXY = x cm2; find, in terms of x, the area of:
PXY = x cm2; find, in terms of x, the area of:
(i) triangle PQR. (ii) trapezium XQRY.
In ![]() PXY and
PXY and ![]() PQR, XY is parallel to QR, so corresponding angles are equal.
PQR, XY is parallel to QR, so corresponding angles are equal.
![]()
Hence, ![]() (By AA similarity criterion)
(By AA similarity criterion)
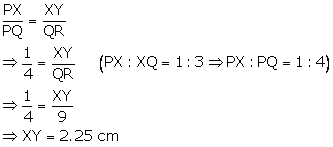
(i) We know that the ratio of areas of two similar triangles is equal to the ratio of the squares of their corresponding sides.
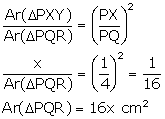
(ii) Ar (trapezium XQRY) = Ar (![]() PQR) - Ar (
PQR) - Ar (![]() PXY)
PXY)
= (16x - x) cm2
= 15x cm2
On a map drawn to a scale of 1: 20000, a rectangular plot of land ABCD is measured as AB = 24 cm and BC = 32 cm. Calculate:
(i) the diagonal distance of the plot in kilometre.
(ii) the area of the plot in sq. km.
Scale :- 1 : 20000
1 cm represents 20000 cm= ![]() = 0.2 km
= 0.2 km
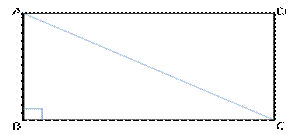
(i)
![]()
= ![]()
= 576 + 1024 = 1600
AC = 40 cm
Actual length of diagonal = 40 ![]() 0.2 km = 8 km
0.2 km = 8 km
(ii)
1 cm represents 0.2 km
1 cm2 represents 0.2 ![]() 0.2
0.2 ![]()
The area of the rectangle ABCD = AB ![]() BC
BC
= 24 ![]() 32 = 768
32 = 768![]()
Actual area of the plot = 0.2 ![]() 0.2
0.2 ![]() 768
768 ![]() = 30.72 km2
= 30.72 km2
The dimensions of the model of a multistoreyed building are 1 m by 60 cm by 1.20 m. If the scale factor is 1: 50, find the actual dimensions of the building. Also, find:
(i) the floor area of a room of the building, if the floor area of the corresponding room in the model is 50 sq. cm.
(ii) the space (volume) inside a room of the model, if the space inside the corresponding room of the building is 90 m3.
The dimensions of the building are calculated as below.
Length = 1 ![]() 50 m = 50 m
50 m = 50 m
Breadth = 0.60 ![]() 50 m = 30 m
50 m = 30 m
Height = 1.20 ![]() 50 m = 60 m
50 m = 60 m
Thus, the actual dimensions of the building are 50 m ![]() 30 m
30 m ![]() 60 m.
60 m.
(i)
Floor area of the room of the building ![]()
(ii)
Volume of the model of the building
![]()
![]()
In a triangle PQR, L and M are two points on the base QR, such that ![]() LPQ =
LPQ = ![]() QRP and
QRP and ![]() RPM =
RPM = ![]() RQP. Prove that:
RQP. Prove that:
(i) ![]()
(ii) ![]()
(iii) ![]()
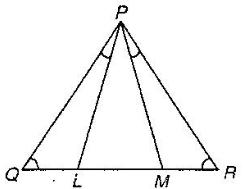
(i)

(ii)

(iii)

A triangle ABC with AB = 3 cm, BC = 6 cm and AC = 4 cm is enlarged to ![]() DEF such that the longest side of
DEF such that the longest side of ![]() DEF = 9 cm. Find the scale factor and hence, the lengths of the other sides of
DEF = 9 cm. Find the scale factor and hence, the lengths of the other sides of ![]() DEF.
DEF.
Triangle ABC is enlarged to DEF. So, the two triangles will be similar.
![]()
Longest side in ![]() ABC = BC = 6 cm
ABC = BC = 6 cm
Corresponding longest side in ![]() DEF = EF = 9 cm
DEF = EF = 9 cm
Scale factor = ![]() = 1.5
= 1.5
Two isosceles triangles have equal vertical angles. Show that the triangles are similar.
If the ratio between the areas of these two triangles is 16: 25, find the ratio between their corresponding altitudes.
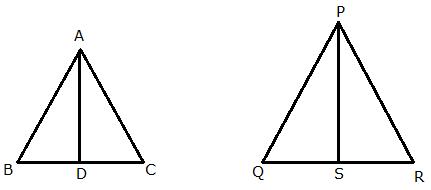
Let ABC and PQR be two isosceles triangles.
Then, ![]()
Also, ![]() A =
A = ![]() P (Given)
P (Given)
![]()
Let AD and PS be the altitude in the respective triangles.
We know that the ratio of areas of two similar triangles is equal to the square of their corresponding altitudes.

In ![]() ABC, AP: PB = 2: 3. PO is parallel to BC and is extended to Q so that CQ is parallel to BA. Find:
ABC, AP: PB = 2: 3. PO is parallel to BC and is extended to Q so that CQ is parallel to BA. Find:
(i) area ![]() APO : area
APO : area ![]() ABC.
ABC.
(ii) area ![]() APO : area
APO : area ![]() CQO.
CQO.
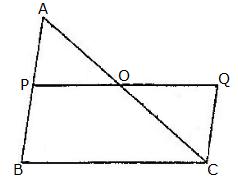
In triangle ABC, PO || BC. Using Basic proportionality theorem,
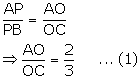
(i)
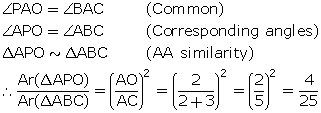
(ii)
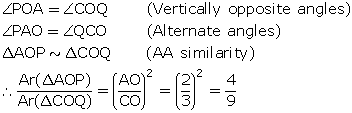
The following figure shows a triangle ABC in which AD and BE are perpendiculars to BC and AC respectively. Show that:
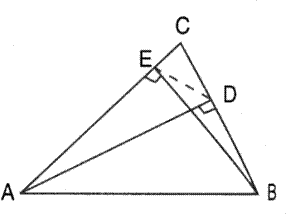

In the given figure, ABC is a triangle with ![]() EDB =
EDB = ![]() ACB. Prove that
ACB. Prove that ![]() ABC
ABC ![]()
![]() EBD. If BE = 6 cm, EC = 4 cm, BD = 5 cm and area of
EBD. If BE = 6 cm, EC = 4 cm, BD = 5 cm and area of ![]() BED = 9 cm2. Calculate the :
BED = 9 cm2. Calculate the :
(i) length of AB.
(ii) area of ![]() ABC.
ABC.
In ![]() ABC and
ABC and ![]() EBD,
EBD,
![]() ACB =
ACB = ![]() EDB (given)
EDB (given)
![]() ABC =
ABC = ![]() EBD (common)
EBD (common)
![]() (by AA- similarity)
(by AA- similarity)
(i) We have, ![]()
(ii) ![]()

In the given figure, ABC is a right angled triangle with m∠BAC = 90°
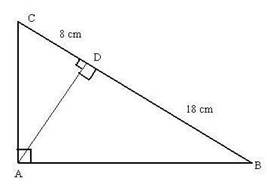
- Prove that ∆ADB ~ ∆CDA
- If BD = 18 cm and CD = 8 cm, find AD.
- Find the ratio of the area of ∆ADB to the area of ∆CDA.

In the given figure, AB and DE are perpendiculars to BC.
Prove that : ΔABC ~ ΔDEC
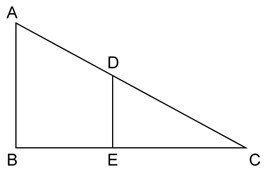

In the given figure, AB and DE are perpendiculars to BC.
If AB = 6 cm, DE = 4 cm and AC = 15 cm. Calculate CD.
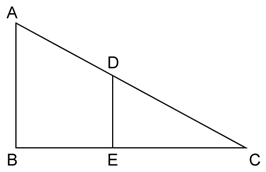

In the given figure, AB and DE are perpendiculars to BC.
Find the ratio of the area of a ΔABC : area of ΔDEC.
ABC is a right angled triangle with ∠ABC = 90°. D is any point on AB and DE is perpendicular to AC. Prove that :
ΔADE ~ ΔACB.
ABC is a right angled triangle with ∠ABC = 90°. D is any point on AB and DE is perpendicular to AC. Prove that :
If AC = 13 cm, BC = 5 cm and AE = 4 cm. Find DE and AD.
ABC is a right angled triangle with ∠ABC = 90°. D is any point on AB and DE is perpendicular to AC. Prove that :
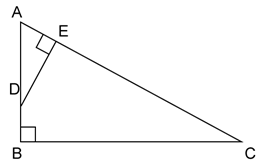
Find, area of ΔADE : area of quadrilateral BCED.

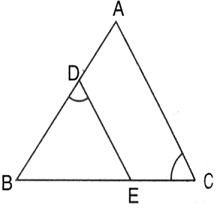
Given: AB || DE and BC || EF. Prove that:
(i) ![]()
(ii) ![]()

(i) In ![]() AGB, DE || AB , by Basic proportionality theorem,
AGB, DE || AB , by Basic proportionality theorem,
![]() .... (1)
.... (1)
In ![]() GBC, EF || BC, by Basic proportionality theorem,
GBC, EF || BC, by Basic proportionality theorem,
![]() .... (2)
.... (2)
From (1) and (2), we get,
![]()
![]()
(ii)
From (i), we have:
![]()
![]()
PQR is a triangle. S is a point on the side QR of ΔPQR such that ∠PSR = ∠QPR. Given QP = 8 cm, PR = 6 cm and SR = 3 cm.
i. Prove ΔPQR ∼ ΔSPR.
ii. Find the lengths of QR and PS.
iii. ![]()

i.
In ∆PQR and ∆SPR,
∠PSR = ∠QPR … given
∠PRQ = ∠PRS … common angle
⇒ ∆PQR ∼ ∆SPR (AA Test)
ii. Find the lengths of QR and PS.
Since ∆PQR ∼ ∆SPR … from (i)
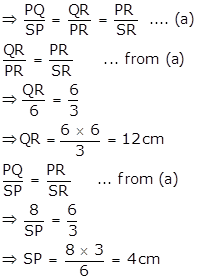
iii.
![]()
No comments:
Post a Comment