Find the slope of the line whose inclination is:
(i) 0![]() (ii) 30
(ii) 30![]()
(iii) 72![]() 30' (iv) 46
30' (iv) 46![]()
(i) Slope = tan 0o = 0
(ii) Slope = tan 30o = ![]()
(iii) Slope = tan 72o 30' = 3.1716
(iv) Slope = tan 46o = 1.0355
Find the inclination of the line whose slope is:
(i) 0 (ii) ![]()
(iii) 0.7646 (iv) 1.0875
(i) Slope = tan ![]() = 0
= 0
![]() = 0o
= 0o
(ii) Slope = tan ![]() =
= ![]()
![]() = 60o
= 60o
(iii) Slope = tan ![]() = 0.7646
= 0.7646
![]() = 37o 24'
= 37o 24'
(iv) Slope = tan ![]() = 1.0875
= 1.0875
![]() = 47o 24'
= 47o 24'
Find the slope of the line passing through the following pairs of points:
(i) (-2, -3) and (1, 2)
(ii) (-4, 0) and origin
(iii) (a, -b) and (b, -a)
We know:
Slope = ![]()
(i) Slope = ![]()
(ii) Slope = ![]()
(iii) Slope = ![]()
Find the slope of the line parallel to AB if:
(i) A = (-2, 4) and B = (0, 6)
(ii) A = (0, -3) and B = (-2, 5)
(i) Slope of AB = ![]()
Slope of the line parallel to AB = Slope of AB = 1
(ii) Slope of AB = ![]()
Slope of the line parallel to AB = Slope of AB = -4
Find the slope of the line perpendicular to AB if:
(i) A = (0, -5) and B = (-2, 4)
(ii) A = (3, -2) and B = (-1, 2)
(i) Slope of AB = ![]()
Slope of the line perpendicular to AB = ![]()

(ii) Slope of AB = ![]()
Slope of the line perpendicular to AB = ![]() 1
1
The line passing through (0, 2) and (-3, -1) is parallel to the line passing through (-1, 5) and (4, a). Find a.
Slope of the line passing through (0, 2) and (-3, -1) = ![]()
Slope of the line passing through (-1, 5) and (4, a) = ![]()
Since, the lines are parallel.

The line passing through (-4, -2) and (2, -3) is perpendicular to the line passing through (a, 5) and (2, -1). Find a.
Slope of the line passing through (-4, -2) and (2, -3) = ![]()
Slope of the line passing through (a, 5) and (2, -1) = ![]()
Since, the lines are perpendicular.
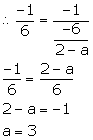
Without using the distance formula, show that the points A (4, -2), B (-4, 4) and C (10, 6) are the vertices of a right-angled triangle.
The given points are A (4, -2), B (-4, 4) and C (10, 6).
![]()
![]()
![]()
It can be seen that:
![]()
Hence, AB ![]() AC.
AC.
Thus, the given points are the vertices of a right-angled triangle.
Without using the distance formula, show that the points A (4, 5), B (1, 2), C (4, 3) and D (7, 6) are the vertices of a parallelogram.
The given points are A (4, 5), B (1, 2), C (4, 3) and D (7, 6).
![]()
![]()
Since, slope of AB = slope of CD
Therefore AB || CD

Since, slope of BC = slope of DA
Therefore, BC || DA
Hence, ABCD is a parallelogram
(-2, 4), (4, 8), (10, 7) and (11, -5) are the vertices of a quadrilateral. Show that the quadrilateral, obtained on joining the mid-points of its sides, is a parallelogram.
Let the given points be A (-2, 4), B (4, 8), C (10, 7) and D (11, -5).
Let P, Q, R and S be the mid-points of AB, BC, CD and DA respectively.
Co-ordinates of P are
![]()
Co-ordinates of Q are
![]()
Co-ordinates of R are
![]()
Co-ordinates of S are
![]()

Since, slope of PQ = Slope of RS, PQ || RS.

Since, slope of QR = Slope of SP, QR || SP.
Hence, PQRS is a parallelogram.
Show that the points P (a, b + c), Q (b, c + a) and R (c, a + b) are collinear.
The points P, Q, R will be collinear if slope of PQ and QR is the same.

Hence, the points P, Q, and R are collinear.
Find x, if the slope of the line joining (x, 2) and (8, -11) is![]() .
.
Let A = (x, 2) and B = (8, -11)
Slope of AB = ![]()
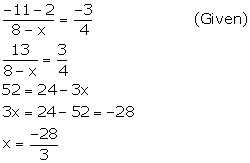
The side AB of an equilateral triangle ABC is parallel to the x-axis. Find the slope of all its sides.

We know that the slope of any line parallel to x-axis is 0.
Therefore, slope of AB = 0
Since, ABC is an equilateral triangle, ![]()
Slope of AC = tan 60o =![]()
Slope of BC = -tan 60o = -![]()
The side AB of a square ABCD is parallel to the x-axis. Find the slopes of all its sides.
Also, find:
(i) the slope of the diagonal AC,
(ii) the slope of the diagonal BD.
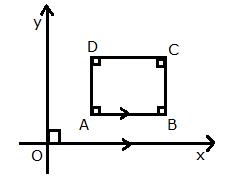
We know that the slope of any line parallel to x-axis is 0.
Therefore, slope of AB = 0
As CD || AB, slope of CD = Slope of AB = 0
As BC ![]() AB, slope of BC =
AB, slope of BC = ![]()
As AD ![]() AB, slope of AD =
AB, slope of AD = ![]()
(i) The diagonal AC makes an angle of 45o with the positive direction of x axis.
![]()
(ii) The diagonal BD makes an angle of -45o with the positive direction of x axis.
A (5, 4), B (-3, -2) and C (1, -8) are the vertices of a triangle ABC. Find:
(i) the slope of the altitude of AB,
(ii) the slope of the median AD, and
(iii) the slope of the line parallel to AC.
Given, A (5, 4), B (-3, -2) and C (1, -8) are the vertices of a triangle ABC.
(i) Slope of AB = ![]()
Slope of the altitude of AB = 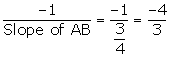
(ii) Since, D is the mid-point of BC.
Co-ordinates of point D are
![]()
Slope of AD = ![]()
(iii) Slope of AC = ![]()
Slope of line parallel to AC = Slope of AC = 3
The slope of the side BC of a rectangle ABCD is![]() . Find:
. Find:
(i) the slope of the side AB,
(ii) the slope of the side AD.
(i) Since, BC is perpendicular to AB,
Slope of AB = 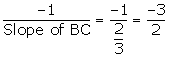
(ii) Since, AD is parallel to BC,
Slope of AD = Slope of BC = ![]()
Find the slope and the inclination of the line AB if:
(i) A = (-3, -2) and B = (1, 2)
(ii) A = (0, ![]() ) and B = (3, 0)
) and B = (3, 0)
(iii) A = (-1, 2![]() ) and B = (-2,
) and B = (-2, ![]() )
)
(i) A = (-3, -2) and B = (1, 2)
Slope of AB = ![]()
Inclination of line AB = ![]() = 45o
= 45o
(ii) A = (0, ![]() ) and B = (3, 0)
) and B = (3, 0)
Slope of AB = ![]()
Inclination of line AB = ![]() = 30o
= 30o
(iii) A = (-1, 2![]() ) and B = (-2,
) and B = (-2, ![]() )
)
Slope of AB = ![]()
Inclination of line AB = ![]() = 60o
= 60o
The points (-3, 2), (2, -1) and (a, 4) are collinear. Find a.
Given, points A (-3, 2), B (2, -1) and C (a, 4) are collinear.
![]() Slope of AB = Slope of BC
Slope of AB = Slope of BC

The points (K, 3), (2, -4) and (-K + 1, -2) are collinear. Find K.
Given, points A (K, 3), B (2, -4) and C (-K + 1, -2) are collinear.
![]() Slope of AB = Slope of BC
Slope of AB = Slope of BC
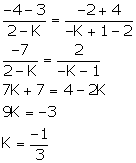
Plot the points A (1, 1), B (4, 7) and C (4, 10) on a graph paper. Connect A and B, and also A and C.
Which segment appears to have the steeper slope, AB or AC?
Justify your conclusion by calculating the slopes of AB and AC.
From the graph, clearly, AC has steeper slope.
Slope of AB = ![]()
Slope of AC = ![]()
The line with greater slope is steeper. Hence, AC has steeper slope.
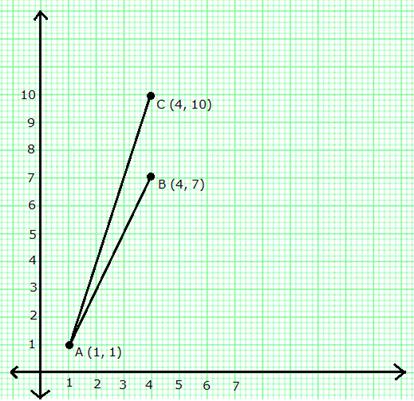
Find the value(s) of k so that PQ will be parallel to RS. Given:
(i) P (2, 4), Q (3, 6), R (8, 1) and S (10, k)
(ii) P (3, -1), Q (7, 11), R (-1, -1) and S (1, k)
(iii) P (5, -1), Q (6, 11), R (6, -4k) and S (7, k2)
Since, PQ || RS,
Slope of PQ = Slope of RS
(i) Slope of PQ = ![]()
Slope of RS = ![]()
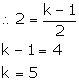
(ii) Slope of PQ = ![]()
Slope of RS = ![]()
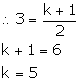
(iii) Slope of PQ = ![]()
Slope of RS = ![]()
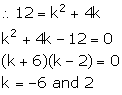
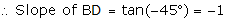
No comments:
Post a Comment