Chapter 13 - Section and Mid-Point Formula Exercise Ex. 13(B)

Question 1

Find the mid-point of the line segment joining the points:

(i) (-6, 7) and (3, 5)

(ii) (5, -3) and (-1, 7)

Solution 1

(i) A (-6, 7) and B (3, 5)

Mid-point of AB = 

(ii) A (5, -3) and B (-1, 7)

Mid-point of AB = 

Question 2

Points A and B have co-ordinates (3, 5) and (x, y) respectively. The mid-point of AB is (2, 3). Find the values of x and y.

Solution 2

Mid-point of AB = (2, 3)

Question 3

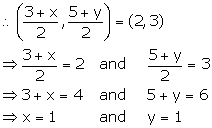
A (5, 3), B (-1, 1) and C (7, -3) are the vertices of triangle ABC. If L is the mid-point of AB and M is the mid-point of AC, show that LM = BC.

Solution 3

Given, L is the mid-point of AB and M is the mid-point of AC.

Co-ordinates of L are

Co-ordinates of M are

Using distance formula, we have:

Question 4

Given M is the mid-point of AB, find the co-ordinates of:

(i) A; if M = (1, 7) and B = (-5, 10)

(ii) B; if A = (3, -1) and M = (-1, 3).

Solution 4

(i) Let the co-ordinates of A be (x, y).

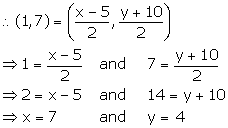
Hence, the co-ordinates of A are (7, 4).

(ii) Let the co-ordinates of B be (x, y).

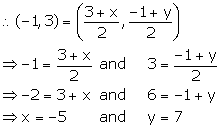
Hence, the co-ordinates of B are (-5, 7).

Question 5

P (-3, 2) is the mid-point of line segment AB as shown in the given figure. Find the co-ordinates of points A and B.

Solution 5

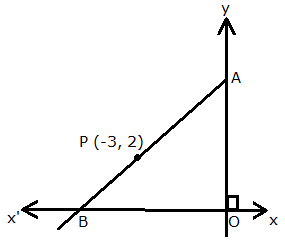
Point A lies on y-axis, so let its co-ordinates be (0, y).

Point B lies on x-axis, so let its co-ordinates be (x, 0).

P (-3, 2) is the mid-point of line segment AB.

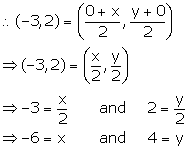
Thus, the co-ordinates of points A and B are (0, 4) and (-6, 0) respectively.

Question 6

In the given figure, P (4, 2) is mid-point of line segment AB. Find the co-ordinates of A and B.

Solution 6

Point A lies on x-axis, so let its co-ordinates be (x, 0).

Point B lies on y-axis, so let its co-ordinates be (0, y).

P (4, 2) is mid-point of line segment AB.

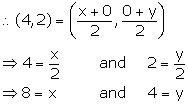
Hence, the co-ordinates of points A and B are (8, 0) and (0, 4) respectively.

Question 7

(-5, 2), (3, -6) and (7, 4) are the vertices of a triangle. Find the lengths of its median through the vertex (3, -6)

Solution 7

Let A (-5, 2), B (3, -6) and C (7, 4) be the vertices of the given triangle.

Let AD be the median through A, BE be the median through B and CF be the median through C.

 

We know that median of a triangle bisects the opposite side.

 

Co-ordinates of point F are

 

Co-ordinates of point D are

 

Co-ordinates of point E are

The median of the triangle through the vertex B(3, -6) is BE

 

Using distance formula,

Question 8

Given a line ABCD in which AB = BC = CD, B = (0, 3) and C = (1, 8). Find the co-ordinates of A and D.

Solution 8

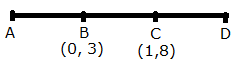
Given, AB = BC = CD

So, B is the mid-point of AC. Let the co-ordinates of point A be (x, y).

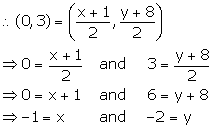
Thus, the co-ordinates of point A are (-1, -2).

Also, C is the mid-point of BD. Let the co-ordinates of point D be (p, q).

Thus, the co-ordinates of point D are (2, 13).

Question 9

One end of the diameter of a circle is (-2, 5). Find the co-ordinates of the other end of it, if the centre of the circle is (2, -1).

Solution 9

We know that the centre is the mid-point of diameter.

Let the required co-ordinates of the other end of mid-point be (x, y).

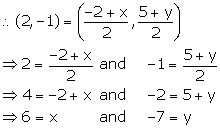
Thus, the required co-ordinates are (6, -7).

Question 10

A (2, 5), B (1, 0), C (-4, 3) and D (-3, 8) are the vertices of a quadrilateral ABCD. Find the co-ordinates of the mid-points of AC and BD.

Give a special name to the quadrilateral.

Solution 10

Co-ordinates of the mid-point of AC are

Co-ordinates of the mid-point of BD are

Since, mid-point of AC = mid-point of BD

Hence, ABCD is a parallelogram.

Question 11

P (4, 2) and Q (-1, 5) are the vertices of a parallelogram PQRS and (-3, 2) are the co-ordinates of the points of intersection of its diagonals. Find the coordinates of R and S.

Solution 11

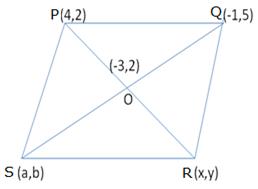
Let the coordinates of R and S be (x,y) and (a,b) respectively.

Mid-point of PR is O.

O(-3,2) = 

-6 = 4 + x, 4 = 2 + y

x = -10 , y = 2

Hence, R = (-10,2)

Similarly, the mid-point of SQ is O.

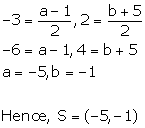
Thus, the coordinates of the point R and S are (-10, 2) and (-5, -1).

Question 12

A (-1, 0), B (1, 3) and D (3, 5) are the vertices of a parallelogram ABCD. Find the co-ordinates of vertex C.

Solution 12

Let the co-ordinates of vertex C be (x, y).

ABCD is a parallelogram.

Mid-point of AC = Mid-point of BD

Thus, the co-ordinates of vertex C is (5, 8).

Question 13

The points (2, -1), (-1, 4) and (-2, 2) are mid-points of the sides of a triangle. Find its vertices.

Solution 13

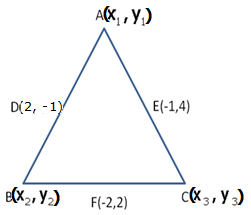
Let A(x₁,y₁), B and C be the co-ordinates of the vertices of ABC.

 

Midpoint of AB, i.e. D

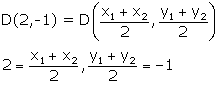
Similarly,

Adding (1), (3) and (5), we get,

 

 

 

 

 

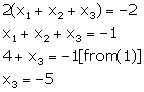
From (3)

From (5)

Adding (2), (4) and (6), we get,

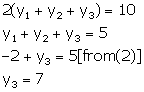
From (4)

From (6)

 

Thus, the co-ordinates of the vertices of ABC are (3, 1), (1, -3) and (-5, 7).

Question 14

Points A (-5, x), B (y, 7) and C (1, -3) are collinear (i.e., lie on the same straight line) such that AB = BC. Calculates the values of x and y.

Solution 14

Given, AB = BC, i.e., B is the mid-point of AC.

Question 15

Points P (a, -4), Q (-2, b) and R (0, 2) are collinear. If Q lies between P and R, such that PR = 2QR, calculate the values of a and b.

Solution 15

Given, PR = 2QR

Now, Q lies between P and R, so, PR = PQ + QR

PQ + QR = 2QR

 PQ = QR

 Q is the mid-point of PR.

Question 16

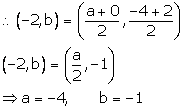
Calculate the co-ordinates of the centroid of a triangle ABC, if A = (7, -2), B = (0, 1) and C = (-1, 4).

Solution 16

Co-ordinates of the centroid of triangle ABC are

Question 17

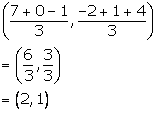
The co-ordinates of the centroid of a PQR are (2, -5). If Q = (-6, 5) and R = (11, 8); calculate the co-ordinates of vertex P.

Solution 17

Let G be the centroid of DPQR whose coordinates are (2, -5) and let (x,y) be the coordinates of vertex P.

Coordinates of G are,

6 = x + 5, -15 = y + 13

x = 1, y = -28

Coordinates of vertex P are (1, -28)

Question 18

A (5, x), B (-4, 3) and C (y, -2) are the vertices of the triangle ABC whose centroid is the origin. Calculate the values of x and y.

Solution 18

Given, centroid of triangle ABC is the origin.