Chapter 24 - Measures of Central Tendency (Mean, Median, Quartiles and Mode) Exercise Ex. 24(C)

Question 1

A student got the following marks in 9 questions of a question paper.

3, 5, 7, 3, 8, 0, 1, 4 and 6.

Find the median of these marks.

Solution 1

Arranging the given data in descending order:

8, 7, 6, 5, 4, 3, 3, 1, 0

The middle term is 4 which is the 5^th term.

Median = 4

Question 2

The weights (in kg) of 10 students of a class are given below:

21, 28.5, 20.5, 24, 25.5, 22, 27.5, 28, 21 and 24.

Find the median of their weights.

Solution 2

Arranging the given data in descending order:

28.5, 28, 27.5, 25.5, 24, 24, 22, 21, 21, 20.5

The middle terms are 24 and 24, 5^th and 6^th terms

Question 3

The marks obtained by 19 students of a class are given below:

27, 36, 22, 31, 25, 26, 33, 24, 37, 32, 29, 28, 36, 35, 27, 26, 32, 35 and 28. Find:

(i) median

(ii) lower quartile

(iii) upper quartile

(iv) interquartile range

Solution 3

Arranging in ascending order:

22, 24, 25, 26, 26, 27, 27, 28, 28, 29, 21, 32, 32, 33, 35, 35, 36, 36, 37

(i) Middle term is 10^th term i.e. 29

Median = 29

(ii) Lower quartile =

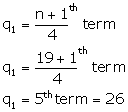
(iii) Upper quartile =

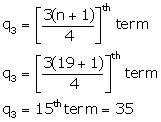
(iv) Interquartile range = q₃ - q₁ =35 - 26 = 9

Question 4

From the following data, find:

(i) Median

(ii) Upper quartile

(iii) Inter-quartile range

25, 10, 40, 88, 45, 60, 77, 36, 18, 95, 56, 65, 7, 0, 38 and 83

Solution 4

Arrange in ascending order:

0, 7, 10, 18, 25, 36, 38, 40, 45, 56, 60, 65, 77, 83, 88, 95

(i) Median is the mean of 8^th and 9^th term

(ii) Upper quartile =

(iii) Interquartile range =

Question 5

The ages of 37 students in a class are given in the following table:

Age (in years)	11	12	13	14	15	16
Frequency	2	4	6	10	8	7

Find the median.

Solution 5

Age (in years)	Frequency	Cumulative Frequency
11	2	2
12	4	6
13	6	12
14	10	22
15	8	30
16	7	37

Number of terms = 37

Median = 

Median = 14

Question 6

The weight of 60 boys are given in the following distribution table:

Weight (kg)	37	38	39	40	41
No. of boys	10	14	18	12	6

Find:

(i) median

(ii) lower quartile

(iii) upper quartile

(iv) interquartile range

Solution 6

Weight (kg) x	no. of boys f	cumulative frequency
37	10	10
38	14	24
39	18	42
40	12	54
41	6	60

Number of terms = 60

(i) median = the mean of the 30^th and the 31^st terms

(ii) lower quartile (Q₁) = 

(iii) upper quartile (Q₃) = 

(iv) Interquartile range = Q₃ - Q₁ = 40 - 38 = 2

Question 7

Estimate the median for the given data by drawing an ogive:

Class	0-10	10-20	20-30	30-40	40-50
frequency	4	9	15	14	8

Solution 7

Class	Frequency	Cumulative Frequency
0-10	4	4
10-20	9	13
20-30	15	28
30-40	14	42
40-50	8	50

Number of terms = 50

Through mark of 25.5 on the y-axis, draw a line parallel to x-axis which meets the curve at A. From A, draw a perpendicular to x-axis, which meets x-axis at B.

The value of B is the median which is 28.

Question 8

By drawing an ogive, estimate the median for the following frequency distribution:

Weight (kg)	10-15	15-20	20-25	25-30	30-35
No. of boys	11	25	12	5	2

Solution 8

Weight (kg)	No. of boys	Cumulative Frequency
10-15	11	11
15-20	25	36
20-25	12	48
25-30	5	53
30-35	2	55

Number of terms = 55

Through mark of 28 on the y-axis, draw a line parallel to x-axis which meets the curve at A. From A, draw a perpendicular to x-axis, which meets x-axis at B.

The value of B is the median which is 18.4 kg

Question 9

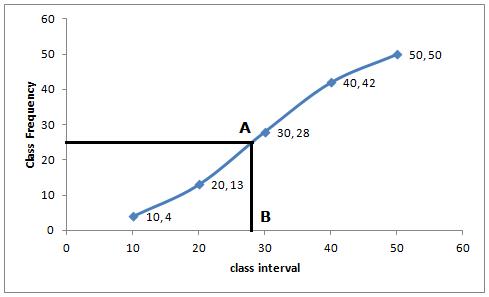
From the following cumulative frequency table, find:

(i) median

(ii) lower quartile

(iii) upper quartile

Marks(less than)	10	20	30	40	50	60	70	80	90	100
Cumulative frequency	5	24	37	40	42	48	70	77	79	80

Solution 9

Marks (less than)	Cumulative frequency
10	5
20	24
30	37
40	40
50	42
60	48
70	70
80	77
90	79
100	80

Number of terms = 80

\Median = 40^th term.

(i) Median = Through 40^th term mark draw a line parallel to the x-axis which meets the curve at A. From A, draw a perpendicular to x-axis which meets it at B.

Value of B is the median = 40

(ii) Lower quartile (Q₁) = 20^th term = 18

(iii) Upper Quartile (Q₃) = 60^th term = 66

Question 10

In a school, 100 pupils have heights as tabulated below:

Height (in cm)	No. of pupils
121 - 130	12
131 - 140	16
141 - 150	30
151 - 160	20
161 - 170	14
171 - 180	8

Find the median height by drawing an ogive.

Solution 10

Height (in cm)	No. of pupils	Cumulative Frequency
121 - 130	12	12
131 - 140	16	28
141 - 150	30	58
151 - 160	20	78
161 - 170	14	92
171 - 180	8	100

Number of terms = 100

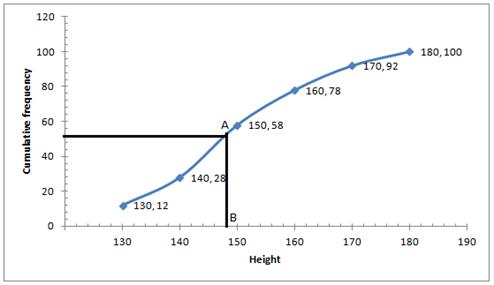
Through 50^th term mark draw a line parallel to the x-axis which meets the curve at A. From A, draw a perpendicular to x-axis which meets it at B.

Value of B is the median = 148

Median height = 148cm