Chapter 12 - Reflection (In x-axis, y-axis, x=a, y=a and the origin ; Invariant Points) Exercise Ex. 12(B)

Question 1

Attempt this question on graph paper.

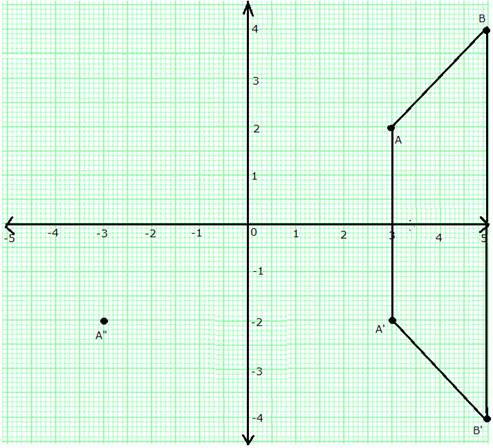
(a) Plot A (3, 2) and B (5, 4) on graph paper. Take 2 cm = 1 unit on both the axes.

(b) Reflect A and B in the x-axis to A' and B' respectively. Plot these points also on the same graph paper.

(c) Write down:

(i) the geometrical name of the figure ABB'A';

(ii) the measure of angle ABB';

(iii) the image of A'' of A, when A is reflected in the origin.

(iv) the single transformation that maps A' to A''.

Solution 1

(c)

(i) From graph, it is clear that ABB'A' is an isosceles trapezium.

(ii) The measure of angle ABB' is 45°.

(iii) A'' = (-3, -2)

(iv) Single transformation that maps A' to A" is the reflection in y-axis.

Question 2

Points (3, 0) and (-1, 0) are invariant points under reflection in the line L₁; points (0, -3) and (0, 1) are invariant points on reflection in line L₂.

(i) Name or write equations for the lines L₁ and L₂.

(ii) Write down the images of the points P (3, 4) and Q (-5, -2) on reflection in line L₁. Name the images as P' and Q' respectively.

(iii) Write down the images of P and Q on reflection in L₂. Name the images as P" and Q" respectively.

(iv) State or describe a single transformation that maps P' onto P".

Solution 2

(i) We know that every point in a line is invariant under the reflection in the same line.

Since points (3, 0) and (-1, 0) lie on the x-axis.

So, (3, 0) and (-1, 0) are invariant under reflection in x-axis.

Hence, the equation of line L₁ is y = 0.

Similarly, (0, -3) and (0, 1) are invariant under reflection in y-axis.

Hence, the equation of line L₂ is x = 0.

(ii) P' = Image of P (3, 4) in L₁ = (3, -4)

Q' = Image of Q (-5, -2) in L₁ = (-5, 2)

(iii) P'' = Image of P (3, 4) in L₂ = (-3, 4)

Q'' = Image of Q (-5, -2) in L₂ = (5, -2)

(iv) Single transformation that maps P' onto P" is reflection in origin.

Question 3

(i) Point P (a, b) is reflected in the x-axis to P' (5, -2). Write down the values of a and b.

(ii) P" is the image of P when reflected in the y-axis. Write down the co-ordinates of P".

(iii) Name a single transformation that maps P' to P".

Solution 3

(i) We know M_x (x, y) = (x, -y)

P' (5, -2) = reflection of P (a, b) in x-axis.

Thus, the co-ordinates of P are (5, 2).

Hence, a = 5 and b = 2.

(ii) P" = image of P (5, 2) reflected in y-axis = (-5, 2)

(iii) Single transformation that maps P' to P" is the reflection in origin.

Question 4

The point (-2, 0) on reflection in a line is mapped to (2, 0) and the point (5, -6) on reflection in the same line is mapped to (-5, -6).

(i) State the name of the mirror line and write its equation.

(ii) State the co-ordinates of the image of (-8, -5) in the mirror line.

Solution 4

(i) We know reflection of a point (x, y) in y-axis is (-x, y).

Hence, the point (-2, 0) when reflected in y-axis is mapped to (2, 0).

Thus, the mirror line is the y-axis and its equation is x = 0.

(ii) Co-ordinates of the image of (-8, -5) in the mirror line (i.e., y-axis) are (8, -5).

Question 5

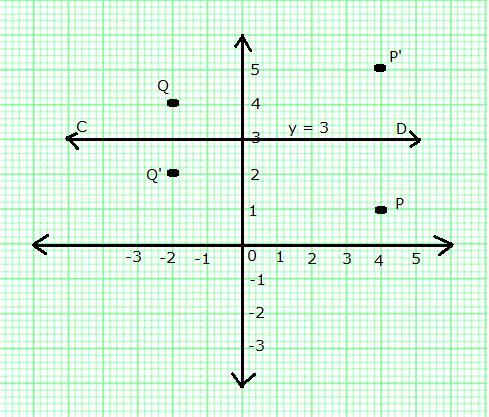
The points P (4, 1) and Q (-2, 4) are reflected in line y = 3. Find the co-ordinates of P', the image of P and Q', the image of Q.

Solution 5

The line y = 3 is a line parallel to x-axis and at a distance of 3 units from it.

Mark points P (4, 1) and Q (-2, 4).

From P, draw a straight line perpendicular to line CD and produce. On this line mark a point P' which is at the same distance above CD as P is below it.

The co-ordinates of P' are (4, 5).

Similarly, from Q, draw a line perpendicular to CD and mark point Q' which is at the same distance below CD as Q is above it.

The co-ordinates of Q' are (-2, 2).

Question 6

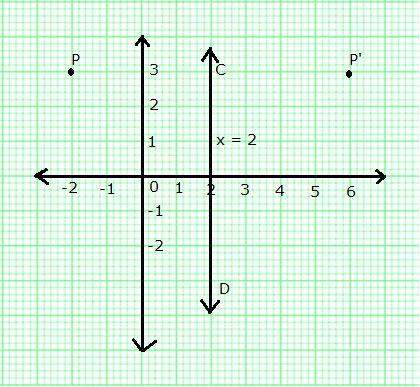
A point P (-2, 3) is reflected in line x = 2 to point P'. Find the coordinates of P'.

Solution 6

The line x = 2 is a line parallel to y-axis and at a distance of 2 units from it.

Mark point P (-2, 3).

From P, draw a straight line perpendicular to line CD and produce. On this line mark a point P' which is at the same distance to the right of CD as P is to the left of it.

The co-ordinates of P' are (6, 3).

Question 7

A point P (a, b) is reflected in the x-axis to P' (2, -3). Write down the values of a and b. P" is the image of P, reflected in the y-axis. Write down the co-ordinates of P". Find the co-ordinates of P''', when P is reflected in the line, parallel to y-axis, such that x = 4.

Solution 7

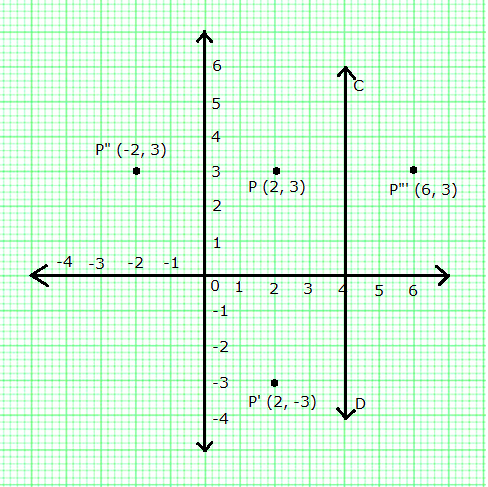
A point P (a, b) is reflected in the x-axis to P' (2, -3).

We know M_x (x, y) = (x, -y)

Thus, co-ordinates of P are (2, 3). Hence, a = 2 and b = 3.

P" = Image of P reflected in the y-axis = (-2, 3)

P''' = Reflection of P in the line (x = 4) = (6, 3)

Question 8

Points A and B have co-ordinates (3, 4) and (0, 2) respectively. Find the image:

(a) A' of A under reflection in the x-axis.

(b) B' of B under reflection in the line AA'.

(c) A" of A under reflection in the y-axis.

(d) B" of B under reflection in the line AA".

Solution 8

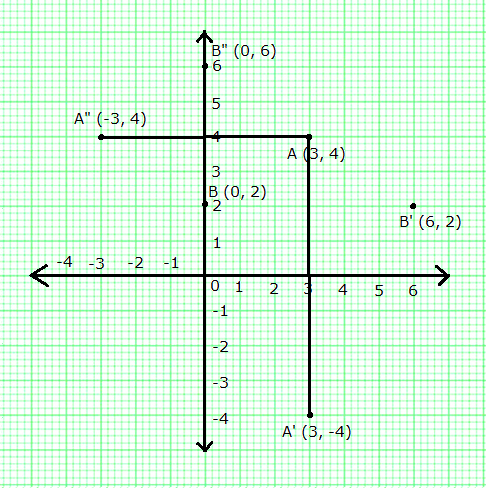
(a) A' = Image of A under reflection in the x-axis = (3, -4)

(b) B' = Image of B under reflection in the line AA' = (6, 2)

(c) A" = Image of A under reflection in the y-axis = (-3, 4)

(d) B" = Image of B under reflection in the line AA" = (0, 6)

Question 9

(i) Plot the points A (3, 5) and B (-2, -4). Use 1 cm = 1 unit on both the axes.

(ii) A' is the image of A when reflected in the x-axis. Write down the co-ordinates of A' and plot it on the graph paper.

(iii) B' is the image of B when reflected in the y-axis, followed by reflection in the origin. Write down the co-ordinates of B' and plot it on the graph paper.

(iv) Write down the geometrical name of the figure AA'BB'.

(v) Name the invariant points under reflection in the x-axis.

Solution 9

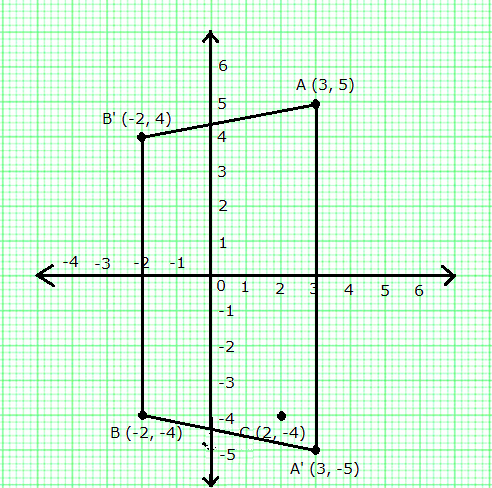
(i) The points A (3, 5) and B (-2, -4) can be plotted on a graph as shown.

(ii) A' = Image of A when reflected in the x-axis = (3, -5)

(iii) C = Image of B when reflected in the y-axis = (2, -4)

B' = Image when C is reflected in the origin = (-2, 4)

(iv) Isosceles trapezium

(v) Any point that remains unaltered under a given transformation is called an invariant.

Thus, the required two points are (3, 0) and (-2, 0).

Question 10

The point P (5, 3) was reflected in the origin to get the image P'.

(a) Write down the co-ordinates of P'.

(b) If M is the foot if the perpendicular from P to the x-axis, find the co-ordinates of M.

(c) If N is the foot if the perpendicular from P' to the x-axis, find the co-ordinates of N.

(d) Name the figure PMP'N.

(e) Find the area of the figure PMP'N.

Solution 10

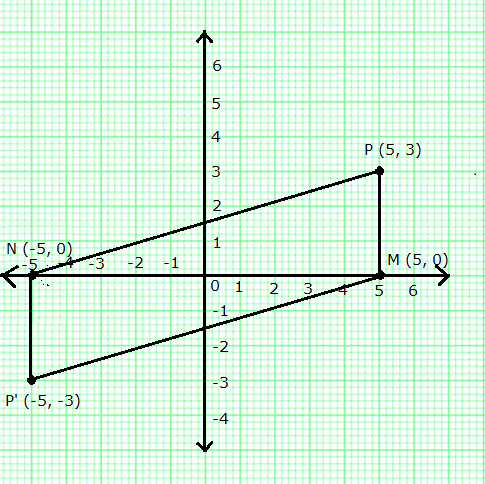
(a) Co-ordinates of P' = (-5, -3)

(b) Co-ordinates of M = (5, 0)

(c) Co-ordinates of N = (-5, 0)

(d) PMP'N is a parallelogram.

(e) Are of PMP'N = 2 (Area of D PMN)

Question 11

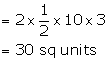
The point P (3, 4) is reflected to P' in the x-axis; and O' is the image of O (the origin) when reflected in the line PP'. Write:

(i) the co-ordinates of P' and O'.

(ii) the length of the segments PP' and OO'.

(iii) the perimeter of the quadrilateral POP'O'.

(iv) the geometrical name of the figure POP'O'.

Solution 11

 

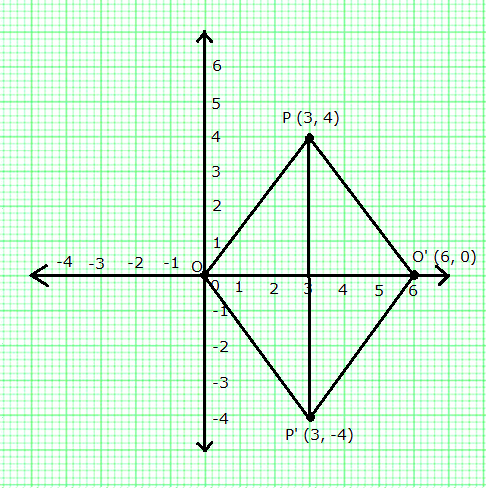
(i) Co-ordinates of P' and O' are (3, -4) and (6, 0) respectively.

(ii) PP' = 8 units and OO' = 6 units.

(iii) From the graph it is clear that all sides of the quadrilateral POP'O' are equal.

In right PO'O,

PO' = 

So, perimeter of quadrilateral POP'O' = 4 PO' = 4  5 units = 20 units

(iv) Quadrilateral POP'O' is a rhombus.

Question 12

A (1, 1), B (5, 1), C (4, 2) and D (2, 2) are vertices of a quadrilateral. Name the quadrilateral ABCD. A, B, C, and D are reflected in the origin on to A', B', C' and D' respectively. Locate A', B', C' and D' on the graph sheet and write their co-ordinates. Are D, A, A' and D' collinear?

Solution 12

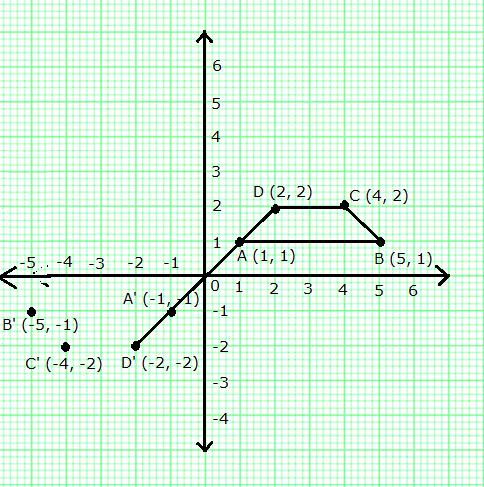
Quadrilateral ABCD is an isosceles trapezium.

Co-ordinates of A', B', C' and D' are A'(-1, -1), B'(-5, -1), C'(-4, -2) and D'(-2, -2) respectively.

It is clear from the graph that D, A, A' and D' are collinear.

Question 13

P and Q have co-ordinates (0, 5) and (-2, 4).

(a) P is invariant when reflected in an axis. Name the axis.

(b) Find the image of Q on reflection in the axis found in (a).

(c) (0, k) on reflection in the origin is invariant. Write the value of k.

(d) Write the co-ordinates of the image of Q, obtained by reflecting it in the origin followed by reflection in x-axis.

Solution 13

(a) Any point that remains unaltered under a given transformation is called an invariant.

 

It is given that P (0, 5) is invariant when reflected in an axis. Clearly, when P is reflected in the y-axis then it will remain invariant. Thus, the required axis is the y-axis.

(b) The co-ordinates of the image of Q (-2, 4) when reflected in y-axis is (2, 4).

(c) (0, k) on reflection in the origin is invariant. We know the reflection of origin in origin is invariant. Thus, k = 0.

(d) Co-ordinates of image of Q (-2, 4) when reflected in origin = (2, -4)

Co-ordinates of image of (2, -4) when reflected in x-axis = (2, 4)

Thus, the co-ordinates of the point are (2, 4).

Question 14

(i) The point P (2, -4) is reflected about the line x = 0 to get the image Q. Find the co-ordinates of Q.

(ii) The point Q is reflected about the line y = 0 to get the image R. Find the co-ordinates or R.

(iii) Name the figure PQR.

(iv) Find the area of figure PQR.

Solution 14

(i) P (2, -4) is reflected in (x = 0) y-axis to get Q.

P(2, -4)  Q (-2, -4)

(ii) Q (-2, -4) is reflected in (y = 0) x-axis to get R.

Q (-2, -4)  R (-2, 4)

(iii) The figure PQR is right angled triangle.

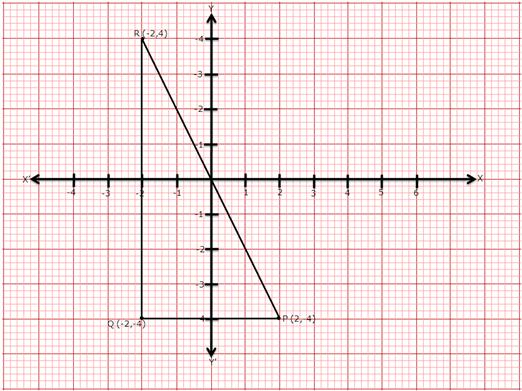
(iv) Area of 

Question 15

Using a graph paper, plot the point A (6, 4) and B (0, 4).

(a) Reflect A and B in the origin to get the image A' and B'.

(b) Write the co-ordinates of A' and B'.

(c) Sate the geometrical name for the figure ABA'B'.

(d) Find its perimeter.

Solution 15

(a)

 

Question 16

Use graph paper for this question.

(Take 2 cm = 1 unit along both side x-axis and y-axis.)

Plot the points O(0,0), A(-4, 4), B(-3, 0) and C(0, -3).

 i. Reflect points A and B on the y-axis and name them A' and B' respectively. Write down their co-ordinates.

 ii. Name the figure OABCB'A'.

 iii. State the line of symmetry of this figure. [Now symmetry is not in course] 

Solution 16

 

 

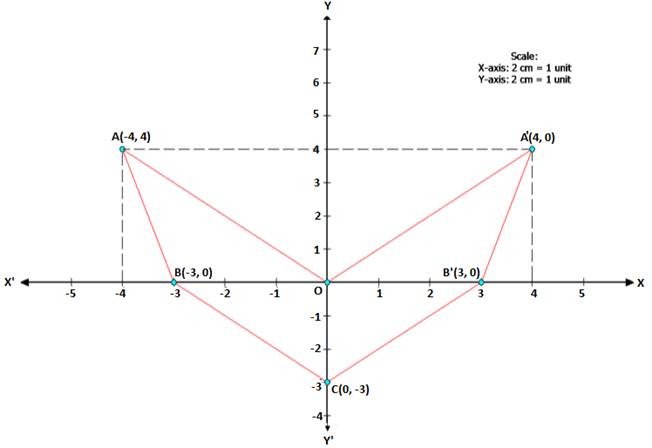
 i. A' = (4, 4) AND B' = (3, 0)

 ii. The figure is an arrow head.

 iii. The y-axis i.e. x = 0 is the line of symmetry of figure OABCB'A'.

Question 17

Use a graph paper for this question: (Take 2cm = 1 unit on both x and y axes) (i) Plot the following points: A(0,4), B(2,3), C(1,1) and D(2,0).

(ii) Reflect points B, C, D on the y-axis and write down their coordinates. Name the images as B', C', D' respectively.

(iii) Join the points A, B, C, D, D', C', B' and A in order, so as to form a closed figure. Write down the equation to the line about which if this closed figure obtained is folded, the two parts of the figure exactly coincide.

Solution 17

(i)Plotting A(0,4), B(2,3), C(1,1) and D(2,0).

 

 

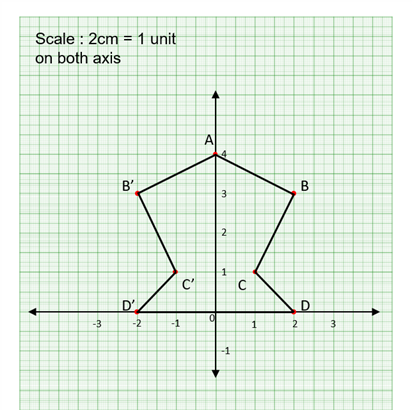
(ii) Reflected points B'(-2,3), C'(-1,1) and D'(-2,0). 

(iii) The figure is symmetrical about x = 0