Chapter 17 - Circles Exercise Ex. 17(C)

Question 1

In the given circle with diametre AB, find the valuv of x.

Solution 1

Question 2

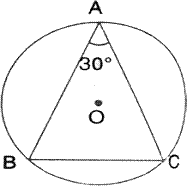
In the given figure, ABC is a triangle in which BAC = 30. Show that BC is equal to the radius of the circum-circle of the triangle ABC, whose centre is O.

Solution 2

Question 3

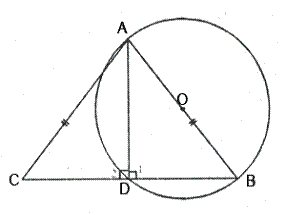
Prove that the circle drawn on any one a the equalside of an isoscele triangle as diameter bisects the base.

Solution 3

Question 4

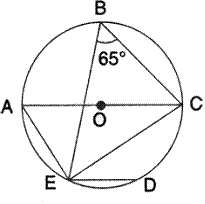
In the given figure, chord ED is parallel to diameter AC of the circle. Given CBE =, calculateDEC.

Solution 4

 

Question 5

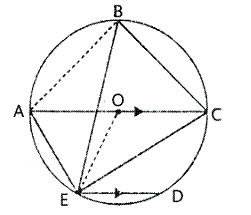
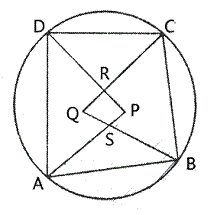
The quadrilateral formed by angle bisectors of a cyclic quadrilateral is also cyclic. Prove it.

Solution 5

Question 6

In the figure, ∠DBC = 58°. BD is a diameter of the circle. Calculate :

(i) ∠BDC

(ii) ∠BEC

(iii) ∠BAC

 

Solution 6

 

Question 7

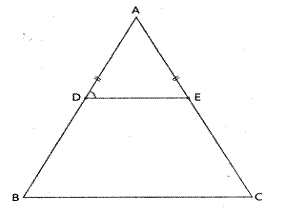
D and E are points on equal sides AB and AC of an isosceles triangle ABC such that AD = AE. Provet that the points B, C, E and D are concyclic.

Solution 7

Question 8

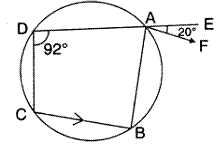
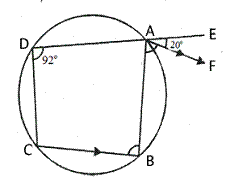
In the given rigure, ABCD is a cyclic eqadrilateral. AF is drawn parallel to CB and DA is produced to point E. If ADC =,FAE =; determineBCD. Given reason in support of your answer.

Solution 8

Question 9

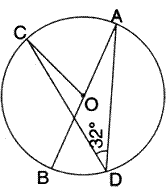
If I is the incentre of triangle ABC and AI when produced meets the cicrumcircle of triangle ABC in points D. ifBAC =and = .calculate:

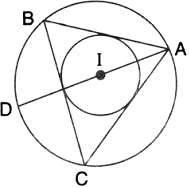
(i)DBC (ii)IBC (iii)BIC.

Solution 9

Question 10

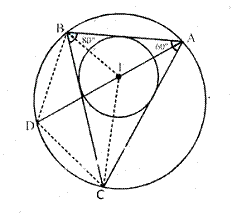
In the given figure, AB = AD = DC = PB and DBC = x^o. Determine, in terms of x :

(i)ABD, (ii)APB.

Hence or otherwise, prove thet AP is parallel to DB.

Solution 10

Question 11

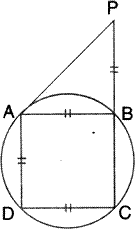
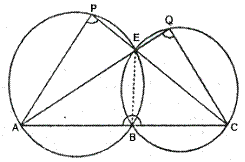
In the given figure; ABC, AEQ and CEP are straight lines. Show thatAPE andCQE are supplementary.

Solution 11

Question 12

In the given, AB is the diameter of the circle with centre O.

IfADC = , find angle BOC.

Solution 12

Question 13

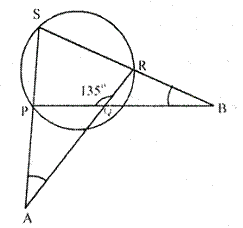
In a cyclic-quadrilateral PQRS, angle PQR =. Sides SP and RQ prouduced meet at point A: whereas sides PQ and SR produced meet at point B.

IfA : B =2 : 1 ; find angles A and B.

Solution 13

Question 14

In the following figure, ABCD is a cyclic quadrilateral in which AD is parallel to BC.

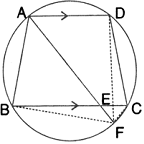
If the bisector of angle A meet BC at point E and the given circle at point F, prove that:

(i) EF = FC (ii) BF = DF

Solution 14

 

Question 15

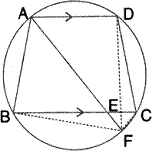
ABCD is a cyclic quadrilateral. Sides AB and DC produced meet at point e; whereas sides BC and AD produced meet at point F.

IfDCF : F : E = 3 : 5 : 4, find the angles of the cyclic quadrilateral ABCD.

Solution 15

Question 16

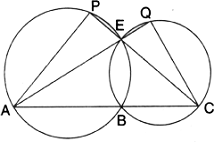
The following figure shows a cicrcle with PR as its diameter. If PQ = 7 cm and QR = 3RS = 6 cm, Find the perimetre of the cyclic quadrilateral PQRS.

Solution 16

Question 17

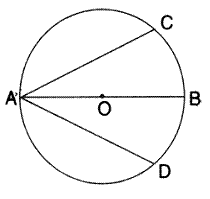
In the following figure, AB is the diameter of a circle with centre O. If chord AC = chord AD ,prove that:

(i) arc BC = arc DB

(ii) AB is bisector ofCAD.

Further if the lenghof arc AC is twice the lengthof arc BC find : (a)BAC (b) ABC

Solution 17

Question 18

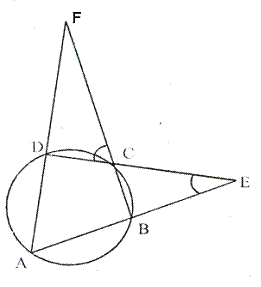
In cyclic quadrilateral ABCD; AD = BC,BAC= andCBD= ; find ;

(i)BCD (ii)BCA

(iii)ABC (iv)ADC

Solution 18

Question 19

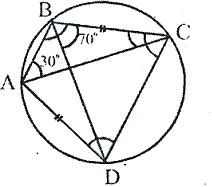
In the given figure, ACE =  and CAF=; find the values of a, b and c.

Solution 19

 

Question 20

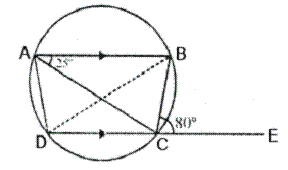
In the given figure, AB is parallel to DC ,BCE = and BAC = 

Find

(i)CAD (ii)CBD (iii)ADC

Solution 20

 

Question 21

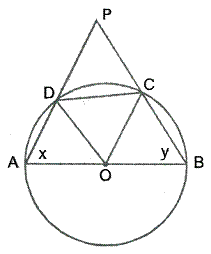
ABCD is a cyclic quadrilalteral of a circle with centre O such that AB is a diameter of this circle and the length of the chord CD is equal to the radius of the circle,.if AD and BC produced meet at P, show that APB =.

Solution 21

Question 22

In the figure, given alongside, CP bisects angle ACB.

Show that DP bisects angle ADB.

Solution 22

Question 23

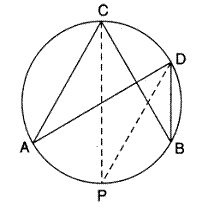
In the figure, given below , AD = BC, BAC =  and CBD = find:

(i)BCD

(ii)BCA

(iii)ABC

(iv)ADB

Solution 23

Question 24

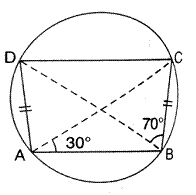
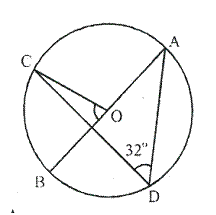
In the given figure, AD is a diameter. O is the centre of the circle. AD is parallel to BC and ∠CBD = 32°.

 

 

Find:

 i. ∠OBD

 ii. ∠AOB

 iii. ∠BED 

Solution 24

i. AD is parallel to BC, i.e., OD is parallel to BC and BD is transversal.

 

 

Question 25

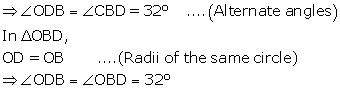
In the figure given, O is the centre of the circle. ∠DAE = 70°. Find giving suitable reasons, the measure of

i. ∠BCD

ii. ∠BOD

iii. ∠OBD

 

Solution 25

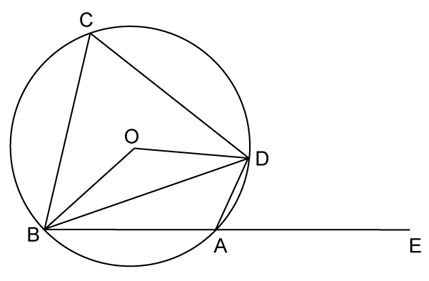
∠DAE and ∠DAB are linear pair

So,

∠DAE + ∠DAB = 180°

 ∴∠DAB = 110°

Also,

∠BCD + ∠DAB = 180°……Opp. Angles of cyclic quadrilateral BADC

 ∴∠BCD = 70°

∠BCD = ∠BOD…angles subtended by an arc on the center and on the circle

 ∴∠BOD = 140°

In ΔBOD,

OB = OD……radii of same circle

So,

∠OBD =∠ODB……isosceles triangle theorem

∠OBD + ∠ODB + ∠BOD = 180°……sum of angles of triangle

2∠OBD = 40° 

∠OBD = 20°