Chapter 24 - Measures of Central Tendency (Mean, Median, Quartiles and Mode) Exercise Ex. 24(B)

Question 1

The following table gives the ages of 50 students of a class. Find the arithmetic mean of their ages.

Age - Years	16 - 18	18 - 20	20 - 22	22- 24	24-26
No. of Students	2	7	21	17	3

Solution 1

Age in years C.I.	xi	Number of students (fi)	xifi
16 - 18	17	2	34
18 - 20	19	7	133
20 - 22	21	21	441
22 - 24	23	17	391
24 - 26	25	3	75
Total		50	1074

Question 2

The following table gives the weekly wages of workers in a factory.

Weekly Wages (Rs)	No. of Workers
50-55	5
55-60	20
60-65	10
65-70	10
70-75	9
75-80	6
80-85	12
85-90	8

Calculate the mean by using:

(i) Direct Method

(ii) Short - Cut Method

Solution 2

(i) Direct Method

Weekly Wages (Rs)	Mid-Value xi	No. of Workers (fi)	fixi
50-55	52.5	5	262.5
55-60	57.5	20	1150.0
60-65	62.5	10	625.0
65-70	67.5	10	675.0
70-75	72.5	9	652.5
75-80	77.5	6	465.0
80-85	82.5	12	990.0
85-90	87.5	8	700.0
Total		80	5520.00

(ii) Short - cut method

Weekly wages (Rs)	No. of workers (fi)	Mid-value xi	A = 72.5 di=x-A	fidi
50-55	5	52.5	-20	-100
55-60	20	57.5	-15	-300
60-65	10	62.5	-10	-100
65-70	10	67.5	-5	-50
70-75	9	A=72.5	0	0
75-80	6	77.5	5	30
80-85	12	82.5	10	120
85-90	8	87.5	15	120
Total	80			-280

Question 3

The following are the marks obtained by 70 boys in a class test:

Marks	No. of boys
30 - 40	10
40 - 50	12
50 - 60	14
60 - 70	12
70 - 80	9
80 - 90	7
90 - 100	6

Calculate the mean by:

(i) Short - cut method

(ii) Step - deviation method

Solution 3

(i) Short - cut method

Marks	No. of boys (fi)	Mid-value xi	A = 65 di=x-A	fidi
30 - 40	10	35	-30	-300
40 - 50	12	45	-20	-240
50 - 60	14	55	-10	-140
60 - 70	12	A = 65	0	0
70 - 80	9	75	10	90
80 - 90	7	85	20	140
90 - 100	6	95	30	180
Total	70			-270

(ii) Step - deviation method

Marks	No. of boys (fi)	Mid-value xi	A = 65	fiui
30 - 40	10	35	-3	-30
40 - 50	12	45	-2	-24
50 - 60	14	55	-1	-14
60 - 70	12	A = 65	0	0
70 - 80	9	75	1	9
80 - 90	7	85	2	14
90 - 100	6	95	3	18
Total	70			-27

Here A = 65 and h = 10

Question 4

Find mean by step - deviation method:

C. I.	63-70	70-77	77-84	84-91	91-98	98-105	105-112
Freq	9	13	27	38	32	16	15

Solution 4

C. I.	Frequency (fi)	Mid-value xi	A = 87.50	fiui
63 - 70	9	66.50	-3	-27
70 - 77	13	73.50	-2	-26
77 - 84	27	80.50	-1	-27
84 - 91	38	A = 87.50	0	0
91 - 98	32	94.50	1	32
98 - 105	16	101.50	2	32
105 - 112	15	108.50	3	45
Total	150			29

Here A = 87.50 and h = 7

Question 5

The mean of the following frequency distribution is . Find the value of 'f'.

C. I.	0 - 10	10 - 20	20 - 30	30 - 40	40 - 50
freq	8	22	31	f	2

Solution 5

C. I.	frequency	Mid-value (xi)	fixi
0-10	8	5	40
10-20	22	15	330
20-30	31	25	775
30-40	f	35	35f
40-50	2	45	90
Total	63+f		1235+35f

Question 6

Using step-deviation method, calculate the mean marks of the following distribution.

C.I	50-55	55-60	60-65	65-70	70-75	75-80	80-85	85-90
Frequency	5	20	10	10	9	6	12	8

Solution 6

Let the assumed mean A= 72.5

C.I	fi	Mid value (xi)	di=xi -; A	fidi
50-55	5	52.5	-20	-100
55-60	20	57.5	-15	-300
60-65	10	62.5	-10	-100
65-70	10	67.5	-5	-50
70-75	9	72.5	0	0
75-80	6	77.5	5	30
80-85	12	82.5	10	120
85-90	8	87.5	15	120
Total	80		-280

Question 7

Using the information given in the adjoining histogram, calculate the mean.

Solution 7

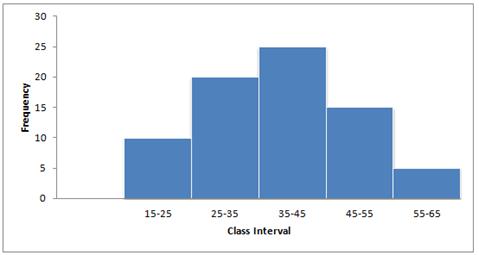
C.I.	Frequency	Mid value x	fx
15-25	10	20	200
25-35	20	30	600
35-45	25	40	1000
45-55	15	50	750
55-65	5	60	300
Total	75		2850

Question 8

If the mean of the following observations is 54, find the value of 'p'.

Class	0 - 20	20 - 40	40 - 60	60 - 80	80 - 100
Frequency	7	p	10	9	13

Solution 8

Class	Frequency (f)	Mid Value (x)	fx
0 - 20	7	10	70
20 - 40	p	30	30p
40 - 60	10	50	500
60 - 80	9	70	630
80 - 100	13	90	1170
Total	39 + p		2370 + 30p

 

Here mean = 54 ..(ii)

from (i) and (ii)

Question 9

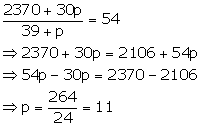
The mean of the following distribution is 62.8 and the sum of all the frequencies is 50. Find the missing frequencies f₁ and f₂.

Class	0-20	20-40	40-60	60-80	80-100	100-120
Freq	5	f1	10	f2	7	8

Solution 9

Class	Freq (f)	Mid value	fx
0-20	5	10	50
20-40	f1	30	30f1
40-60	10	50	500
60-80	f2	70	70f2
80-100	7	90	630
100-120	8	110	880
Total	30+f1+f2		2060+30f1+70f2

Now,  and 

from (i)

using (i) and (ii)

Question 10

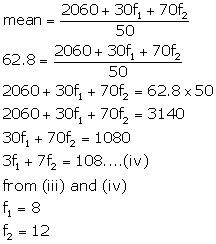
Calculate the mean of the distribution, given below, using the short cut method :

 

Mark	11-20	21-30	31-40	41-50	51-60	61-70	71-80
No. of students	2	6	10	12	9	7	4

 

Solution 10