Chapter 22 - Heights and Distances Exercise Ex. 22(A)

Question 1

The height of a tree is times the length of its shadow. Find the angle of elevation of the sun.

Solution 1

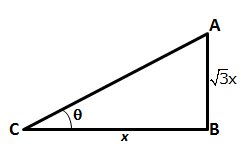
Let the length of the shadow of the tree be x m.

 Height of the tree = m

If is the angle of elevation of the sun, then

Question 2

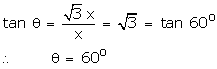
The angle of elevation of the top of a tower from a point on the ground and at a distance of 160 m from its foot, is found to be 60^o. Find the height of the tower.

Solution 2

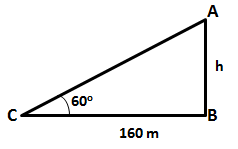
Let the height of the tower be h m.

Given that angle of elevation is 60^o

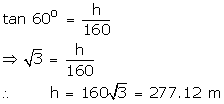
So, height of the tower is 277.12 m.

Question 3

A ladder is placed along a wall such that its upper end is resting against a vertical wall. The foot of the ladder is 2.4 m from the wall and the ladder is making an angle of 68^o with the ground. Find the height, upto which the ladder reaches.

Solution 3

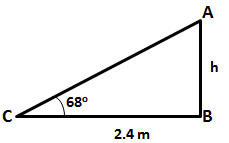
Let the height upto which the ladder reaches be h m.

Given that angle of elevation is 68^o

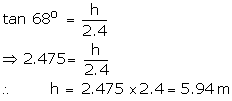
So, the ladder reaches upto a height of 5.94 m.

Question 4

Two persons are standing on the opposite sides of a tower. They observe the angles of elevation of the top of the tower to be 30^o and 38^o respectively. Find the distance between them, if the height of the tower is 50 m.

Solution 4

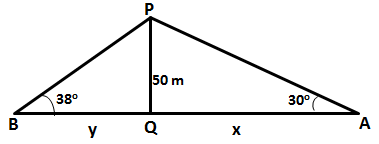
Let one person A be at a distance x and the second person B be at a distance of y from the foot of the tower.

Given that angle of elevation of A is 30^o

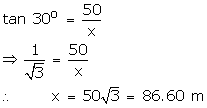
The angle of elevation of B is 38^o

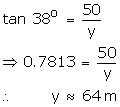
So, distance between A and B is x + y = 150.6 m

Question 5

A kite is attached to a string. Find the length of the string, when the height of the kite is 60 m and the string makes an angle 30^o with the ground.

Solution 5

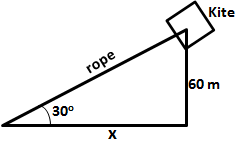
Let the length of the rope be x m.

Now,

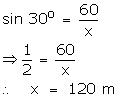
So, the length of the rope is 120m.

Question 6

A boy, 1.6 m tall, is 20 m away from a tower and observes the angle of elevation of the top of the tower to be (i) 45^o, (ii) 60^o. Find the height of the tower in each case.

Solution 6

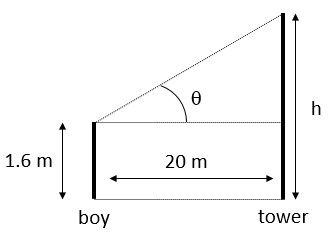
Let the height of the tower be h m.

(i) Here 

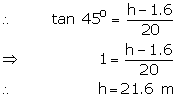
So, height of the tower is 21.6 m.

(ii) Here 

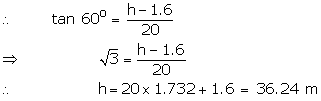
So, height of the tower is 36.24 m.

Question 7

The upper part of a tree, broken over by the wind, makes an angle of 45^o with the ground and the distance from the root to the point where the top of the tree touches the ground is 15 m. What was the height of the tree before it was broken?

Solution 7

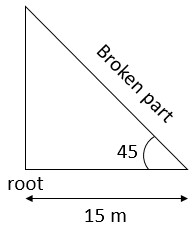
Let the height of the tree after breaking be h m.

Here 

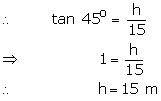
Now, length of the tree broken by the wind = 

So, height of the tree before it was broken is (15 + 21.21) m = 36.21 m.

Question 8

The angle of elevation of the top of an unfinished tower at a point distance 80 m from its base is 30^o. How much higher must the tower be raised so that its angle of elevation at the same point may be 60^o?

Solution 8

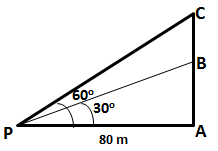
Let AB be the unfinished tower and C be the top of the tower when finished. Let P be a point 80 m from the foot A.

In BAP,

In CAP,

Therefore, the tower must be raised by (138.56 - 46.19)m = 92.37 m

Question 9

At a particular time, when the sun's altitude is 30^o, the length of the shadow of a vertical tower is 45 m. Calculate

(i) the length of the tower.

(ii) the length of the shadow of the same tower, when the sun's altitude is

(a) 45^o (b) 60^o

Solution 9

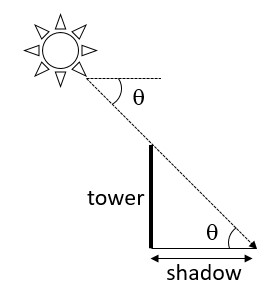
Let the length of the tower be h m.

(i) Here 

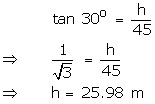
Hence the length of the tower is 25.98 m.

(ii) Let the length of the shadow be x m.

(a) Here, 

Hence the length of the shadow is 25.98 m

(b) Here, 

Hence the length of the shadow is 15 m.

Question 10

Two vertical poles are on either side of a road. A 30 m long ladder is placed between the two poles. When the ladder rests against one pole, it makes angle 32^o24' with the pole and when it is turned to rest against another pole, it makes angle 32^o24' with the road. Calculate the width of the road.

Solution 10

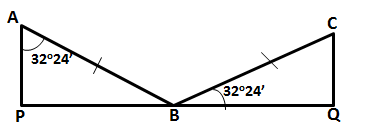
Let AB be the ladder and ABP = 32^o24'.

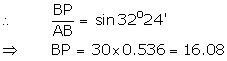
When rotated, let the ladder be AC and CAQ = 32^o24'.

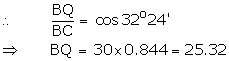
Hence, width of the road = (16.08 + 25.32) = 41.4 m

Question 11

Two climbers are at points A and B on a vertical cliff face. To an observer C, 40m from the foot of the cliff, on the level ground, A is at an elevation of 48^o and B of 57^o. What is the distance between the climbers?

Solution 11

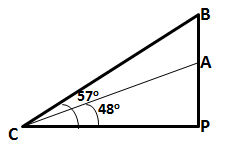
Let P be the foot of the cliff on level ground.

Then, ACP = 48^o and BCP = 57^o

Hence, distance between the climbers = AB = BP - AP = 17.16 m

Question 12

A man stands 9 m away from a flag-pole. He observes that angle of elevation of the top of the pole is 28^o and the angle of depression of the bottom of the pole is 13^o. Calculate the height of the pole.

Solution 12

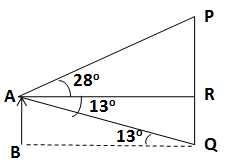
Let AB be the man and PQ be the flag-pole.

Given, AR = 9 m.

Also, PAR = 28^o and QAR = 13^o

Hence, height of the pole = PR + RQ = 6.867 m

Question 13

From the top of a cliff 92 m high, the angle of depression of a buoy is 20^o. Calculate, to the nearest metre, the distance of the buoy from the foot of the cliff.

Solution 13

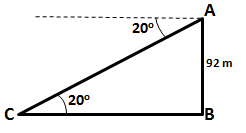
Let AB be the cliff and C be the buoy.

Given, AB = 92 m.

Also, ACB = 20^o

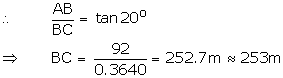
Hence, the buoy is at a distance of 253 m from the foot of the cliff.