Complete the following table:
Point | Transformation | Image |
(5, -7) | (-5, 7) | |
(4, 2) | Reflection in x-axis | |
Reflection in y-axis | (0, 6) | |
(6, -6) | (-6, 6) | |
(4, -8) | (-4, -8) |
Point | Transformation | Image |
(5, -7) | Reflection in origin | (-5, 7) |
(4, 2) | Reflection in x-axis | (4, -2) |
(0, 6) | Reflection in y-axis | (0, 6) |
(6, -6) | Reflection in origin | (-6, 6) |
(4, -8) | Reflection in y-axis | (-4, -8) |
A point P is its own image under the reflection in a line l. Describe the position of point the P with respect to the line l.
Since, the point P is its own image under the reflection in the line l. So, point P is an
invariant point.
Hence, the position of point P remains unaltered.
State the co-ordinates of the following points under reflection in x-axis:
(i) (3, 2)
(ii) (-5, 4)
(iii) (0, 0)
(i) (3, 2)
The co-ordinate of the given point under reflection in the x-axis is (3, -2).
(ii) (-5, 4)
The co-ordinate of the given point under reflection in the x-axis is (-5, -4).
(iii) (0, 0)
The co-ordinate of the given point under reflection in the x-axis is (0, 0).
State the co-ordinates of the following points under reflection in y-axis:
(i) (6, -3)
(ii) (-1, 0)
(iii) (-8, -2)
(i) (6, -3)
The co-ordinate of the given point under reflection in the y-axis is (-6, -3).
(ii) (-1, 0)
The co-ordinate of the given point under reflection in the y-axis is (1, 0).
(iii) (-8, -2)
The co-ordinate of the given point under reflection in the y-axis is (8, -2).
State the co-ordinates of the following points under reflection in origin:
(i) (-2, -4)
(ii) (-2, 7)
(iii) (0, 0)
(i) (-2, -4)
The co-ordinate of the given point under reflection in origin is (2, 4).
(ii) (-2, 7)
The co-ordinate of the given point under reflection in origin is (2, -7).
(iii) (0, 0)
The co-ordinate of the given point under reflection in origin is (0, 0).
State the co-ordinates of the following points under reflection in the line x = 0:
(i) (-6, 4)
(ii) (0, 5)
(iii) (3, -4)
(i) (-6, 4)
The co-ordinate of the given point under reflection in the line x = 0 is (6, 4).
(ii) (0, 5)
The co-ordinate of the given point under reflection in the line x = 0 is (0, 5).
(iii) (3, -4)
The co-ordinate of the given point under reflection in the line x = 0 is (-3, -4).
State the co-ordinates of the following points under reflection in the line y = 0:
(i) (-3, 0)
(ii) (8, -5)
(iii) (-1, -3)
(i) (-3, 0)
The co-ordinate of the given point under reflection in the line y = 0 is (-3, 0).
(ii) (8, -5)
The co-ordinate of the given point under reflection in the line y = 0 is (8, 5).
(iii) (-1, -3)
The co-ordinate of the given point under reflection in the line y = 0 is (-1, 3).
A point P is reflected in the x-axis. Co-ordinates of its image are (-4, 5).
(i) Find the co-ordinates of P.
(ii) Find the co-ordinates of the image of P under reflection in the y-axis.
(i) Since, Mx (-4, -5) = (-4, 5)
So, the co-ordinates of P are (-4, -5).
(ii) Co-ordinates of the image of P under reflection in the y-axis (4, -5).
A point P is reflected in the origin. Co-ordinates of its image are (-2, 7).
(i) Find the co-ordinates of P.
(ii) Find the co-ordinates of the image of P under reflection in the x-axis.
(i) Since, MO (2, -7) = (-2, 7)
So, the co-ordinates of P are (2, -7).
(ii) Co-ordinates of the image of P under reflection in the x-axis (2, 7).
The point (a, b) is first reflected in the origin and then reflected in the y-axis to P'. If P' has co-ordinates (4, 6); evaluate a and b.
MO (a, b) = (-a, -b)
My (-a, -b) = (a, -b)
Thus, we get the co-ordinates of the point P' as (a, -b). It is given that the
co-ordinates of P' are (4, 6).
On comparing the two points, we get,
a = 4 and b = -6
The point P (x, y) is first reflected in the x-axis and reflected in the origin to P'. If P' has co-ordinates (-8, 5); evaluate x and y.
Mx (x, y) = (x, -y)
MO (x, -y) = (-x, y)
Thus, we get the co-ordinates of the point P' as (-x, y). It is given that the
co-ordinates of P' are (-8, 5).
On comparing the two points, we get,
x = 8 and y = 5
The point A (-3, 2) is reflected in the x-axis to the point A'. Point A' is then reflected in the origin to point A''.
(i) Write down the co-ordinates of A''.
(ii) Write down a single transformation that maps A onto A''.
(i) The reflection in x-axis is given by Mx (x, y) = (x, -y).
A' = reflection of A (-3, 2) in the x- axis = (-3, -2).
The reflection in origin is given by MO (x, y) = (-x, -y).
A'' = reflection of A' (-3, -2) in the origin = (3, 2)
(ii) The reflection in y-axis is given by My (x, y) = (-x, y).
The reflection of A (-3, 2) in y-axis is (3, 2).
Thus, the required single transformation is the reflection of A in the y-axis to the point A''.
The point A (4, 6) is first reflected in the origin to point A'. Point A' is then reflected in the y-axis to the point A''.
(i) Write down the co-ordinates of A''.
(ii) Write down a single transformation that maps A onto A''.
(i) The reflection in origin is given by MO (x, y) = (-x, -y).
A' = reflection of A (4, 6) in the origin = (-4, -6)
The reflection in y-axis is given by My (x, y) = (-x, y).
A'' = reflection of A' (-4, -6) in the y-axis = (4, -6)
(ii) The reflection in x-axis is given by Mx (x, y) = (x, -y).
The reflection of A (4, 6) in x-axis is (4, -6).
Thus, the required single transformation is the reflection of A in the x-axis to the point A''.
The triangle ABC, where A is (2, 6), B is (-3, 5) and C is (4, 7), is reflected in the y-axis to triangle A'B'C'. Triangle A'B'C' is then reflected in the origin to triangle A''B''C''.
(i) Write down the co-ordinates of A'', B'' and C''.
(ii) Write down a single transformation that maps triangle ABC onto triangle A''B''C''.
(i) Reflection in y-axis is given by My (x, y) = (-x, y)
![]() A' = Reflection of A (2, 6) in y-axis = (-2, 6)
A' = Reflection of A (2, 6) in y-axis = (-2, 6)
Similarly, B' = (3, 5) and C' = (-4, 7)
Reflection in origin is given by MO (x, y) = (-x, -y)
![]() A'' = Reflection of A' (-2, 6) in origin = (2, -6)
A'' = Reflection of A' (-2, 6) in origin = (2, -6)
Similarly, B'' = (-3, -5) and C'' = (4, -7)
(ii) A single transformation which maps triangle ABC to triangle A''B''C'' is
reflection in x-axis.
P and Q have co-ordinates (-2, 3) and (5, 4) respectively. Reflect P in the x-axis to P' and Q in the y-axis to Q'. State the co-ordinates of P' and Q'.
Reflection in x-axis is given by Mx (x, y) = (x, -y)
P' = Reflection of P(-2, 3) in x-axis = (-2, -3)
Reflection in y-axis is given by My (x, y) = (-x, y)
Q' = Reflection of Q(5, 4) in y-axis = (-5, 4)
Thus, the co-ordinates of points P' and Q' are (-2, -3) and (-5, 4) respectively.
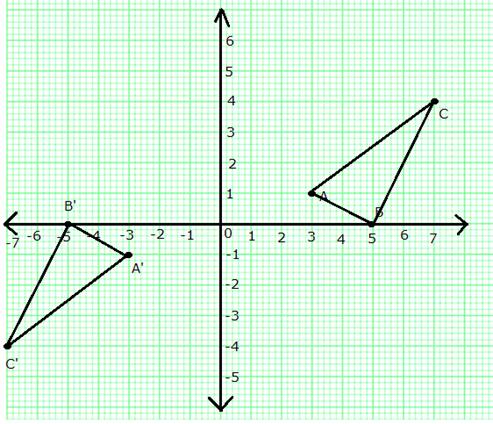
On a graph paper, plot the triangle ABC, whose vertices are at points A (3, 1), B (5, 0) and C (7, 4).
On the same diagram, draw the image of the triangle ABC under reflection in the origin O (0, 0).
The graph shows triangle ABC and triangle A'B'C' which is obtained when ABC is
reflected in the origin.
Point A (4, -1) is reflected as A' in the y-axis. Point B on reflection in the x-axis is mapped as B' (-2, 5). Write down the co-ordinates of A' and B.
Reflection in y-axis is given by My (x, y) = (-x, y)
A' = Reflection of A(4, -1) in y-axis = (-4, -1)
Reflection in x-axis is given by Mx (x, y) = (x, -y)
B' = Reflection of B in x-axis = (-2, 5)
Thus, B = (-2, -5)
The point (-5, 0) on reflection in a line is mapped as (5, 0) and the point (-2, -6) on reflection in the same line is mapped as (2, -6).
(a) Name the line of reflection.
(b) Write down the co-ordinates of the image of (5, -8) in the line obtained in (a).
(a) We know that reflection in the line x = 0 is the reflection in the y-axis.
It is given that:
Point (-5, 0) on reflection in a line is mapped as (5, 0).
Point (-2, -6) on reflection in the same line is mapped as (2, -6).
Hence, the line of reflection is x = 0.
(b) It is known that My (x, y) = (-x, y)
Co-ordinates of the image of (5, -8) in the line x = 0 are (-5, -8).
No comments:
Post a Comment