Chapter 14 - Equation of a Line Exercise Ex. 14(A)

Question 1

Find, which of the following points lie on the line x - 2y + 5 = 0:

(i) (1, 3) (ii) (0, 5)

(iii) (-5, 0) (iv) (5, 5)

(v) (2, -1.5) (vi) (-2, -1.5)

Solution 1

The given line is x - 2y + 5 = 0.

(i) Substituting x = 1 and y = 3 in the given equation, we have:

L.H.S. = 1 - 2  3 + 5 = 1 - 6 + 5 = 6 - 6 = 0 = R.H.S.

Thus, the point (1, 3) lies on the given line.

 

(ii) Substituting x = 0 and y = 5 in the given equation, we have:

L.H.S. = 0 - 2  5 + 5 = -10 + 5 = -5  R.H.S.

Thus, the point (0, 5) does not lie on the given line.

 

(iii) Substituting x = -5 and y = 0 in the given equation, we have:

L.H.S. = -5 - 2  0 + 5 = -5 - 0 + 5 = 5 - 5 = 0 = R.H.S.

Thus, the point (-5, 0) lie on the given line.

 

(iv) Substituting x = 5 and y = 5 in the given equation, we have:

L.H.S. = 5 - 2  5 + 5 = 5 - 10 + 5 = 10 - 10 = 0 = R.H.S.

Thus, the point (5, 5) lies on the given line.

 

(v) Substituting x = 2 and y = -1.5 in the given equation, we have:

L.H.S. = 2 - 2  (-1.5) + 5 = 2 + 3 + 5 = 10  R.H.S.

Thus, the point (2, -1.5) does not lie on the given line.

 

(vi) Substituting x = -2 and y = -1.5 in the given equation, we have:

L.H.S. = -2 - 2  (-1.5) + 5 = -2 + 3 + 5 = 6  R.H.S.

Thus, the point (-2, -1.5) does not lie on the given line.

Question 2

State, true or false:

(i) the line  passes through the point (2, 3).

(ii) the line  passes through the point (4, -6).

(iii) the point (8, 7) lies on the line y - 7 = 0.

(iv) the point (-3, 0) lies on the line x + 3 = 0.

(v) if the point (2, a) lies on the line 2x - y = 3, then a = 5.

Solution 2

(i) The given line is 

Substituting x = 2 and y = 3 in the given equation,

Thus, the given statement is false.

(ii) The given line is 

Substituting x = 4 and y = -6 in the given equation,

Thus, the given statement is true.

(iii) L.H.S = y - 7 = 7 - 7 = 0 = R.H.S.

Thus, the point (8, 7) lies on the line y - 7 = 0.

The given statement is true.

(iv) L.H.S. = x + 3 = -3 + 3 = 0 = R.H.S

Thus, the point (-3, 0) lies on the line x + 3 = 0.

The given statement is true.

(v) The point (2, a) lies on the line 2x - y = 3.

 2(2) - a = 3

4 - a = 3

a = 4 - 3 = 1

Thus, the given statement is false.

Question 3

The line given by the equation  passes through the point (k, 6); calculate the value of k.

Solution 3

Given, the line given by the equation  passes through the point (k, 6).

Substituting x = k and y = 6 in the given equation, we have:

Question 4

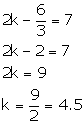
For what value of k will the point (3, -k) lie on the line 9x + 4y = 3?

Solution 4

The given equation of the line is 9x + 4y = 3.

Put x = 3 and y = -k, we have:

9(3) + 4(-k) = 3

27 - 4k = 3

4k = 27 - 3 = 24

k = 6

Question 5

The line  contains the point (m, 2m - 1); calculate the value of m.

Solution 5

The equation of the given line is 

Putting x = m, y = 2m - 1, we have:

Question 6

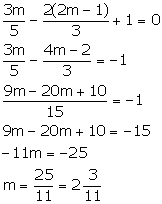
Does the line 3x - 5y = 6 bisect the join of (5, -2) and (-1, 2)?

Solution 6

The given line will bisect the join of A (5, -2) and B (-1, 2), if the co-ordinates of the mid-point of AB satisfy the equation of the line.

The co-ordinates of the mid-point of AB are

Substituting x = 2 and y = 0 in the given equation, we have:

L.H.S. = 3x - 5y = 3(2) - 5(0) = 6 - 0 = 6 = R.H.S.

Hence, the line 3x - 5y = 6 bisect the join of (5, -2) and (-1, 2).

Question 7

(i) The line y = 3x - 2 bisects the join of (a, 3) and (2, -5), find the value of a.

(ii) The line x - 6y + 11 = 0 bisects the join of (8, -1) and (0, k). Find the value of k.

Solution 7

(i) The given line bisects the join of A (a, 3) and B (2, -5), so the co-ordinates of the mid-point of AB will satisfy the equation of the line.

The co-ordinates of the mid-point of AB are

Substituting x =  and y = -1 in the given equation, we have:

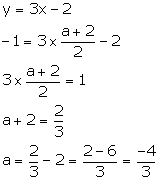
(ii) The given line bisects the join of A (8, -1) and B (0, k), so the co-ordinates of the mid-point of AB will satisfy the equation of the line.

The co-ordinates of the mid-point of AB are

Substituting x = 4 and y =  in the given equation, we have:

Question 8

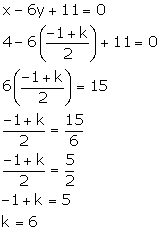
(i) The point (-3, 2) lies on the line ax + 3y + 6 = 0, calculate the value of a.

(ii) The line y = mx + 8 contains the point (-4, 4), calculate the value of m.

Solution 8

(i) Given, the point (-3, 2) lies on the line ax + 3y + 6 = 0.

Substituting x = -3 and y = 2 in the given equation, we have:

a(-3) + 3(2) + 6 = 0

-3a + 12 = 0

3a = 12

a = 4

(ii) Given, the line y = mx + 8 contains the point (-4, 4).

Substituting x = -4 and y = 4 in the given equation, we have:

4 = -4m + 8

4m = 4

m = 1

Question 9

The point P divides the join of (2, 1) and (-3, 6) in the ratio 2: 3. Does P lie on the line x - 5y + 15 = 0?

Solution 9

Given, the point P divides the join of (2, 1) and (-3, 6) in the ratio 2: 3.

Co-ordinates of the point P are

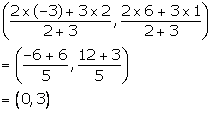
Substituting x = 0 and y = 3 in the given equation, we have:

L.H.S. = 0 - 5(3) + 15 = -15 + 15 = 0 = R.H.S.

Hence, the point P lies on the line x - 5y + 15 = 0.

Question 10

The line segment joining the points (5, -4) and (2, 2) is divided by the point Q in the ratio 1: 2. Does the line x - 2y = 0 contain Q?

Solution 10

Given, the line segment joining the points (5, -4) and (2, 2) is divided by the point Q in the ratio 1: 2.

Co-ordinates of the point Q are

Substituting x = 4 and y = -2 in the given equation, we have:

L.H.S. = x - 2y = 4 - 2(-2) = 4 + 4 = 8  R.H.S.

Hence, the given line does not contain point Q.

Question 11

Find the point of intersection of the lines:

4x + 3y = 1 and 3x - y + 9 = 0. If this point lies on the line (2k - 1)x - 2y = 4; find the value of k.

Solution 11

Consider the given equations:

4x + 3y = 1 ....(1)

3x - y + 9 = 0 ....(2)

Multiplying (2) with 3, we have:

9x - 3y = -27 ....(3)

Adding (1) and (3), we get,

13x = -26

x = -2

 

From (2), y = 3x + 9 = -6 + 9 = 3

 

Thus, the point of intersection of the given lines (1) and (2) is (-2, 3).

 

The point (-2, 3) lies on the line (2k - 1)x - 2y = 4.

 (2k - 1)(-2) - 2(3) = 4

-4k + 2 - 6 = 4

-4k = 8

k = -2

Question 12

Show that the lines 2x + 5y = 1, x - 3y = 6 and x + 5y + 2 = 0 are concurrent.

Solution 12

We know that two or more lines are said to be concurrent if they intersect at a single point.

 

We first find the point of intersection of the first two lines.

2x + 5y = 1 ....(1)

x - 3y = 6 ....(2)

 

Multiplying (2) by 2, we get,

2x - 6y = 12 ....(3)

 

Subtracting (3) from (1), we get,

11y = -11

y = -1

 

From (2), x = 6 + 3y = 6 - 3 = 3

 

So, the point of intersection of the first two lines is (3, -1).

If this point lie on the third line, i.e., x + 5y + 2 = 0, then the given lines will be concurrent.

 

Substituting x = 3 and y = -1, we have:

L.H.S. = x + 5y + 2 = 3 + 5(-1) + 2 = 5 - 5 = 0 = R.H.S.

 

Thus, (3, -1) also lie on the third line.

Hence, the given lines are concurrent.