Show that (x - 1) is a factor of x3 - 7x2 + 14x - 8. Hence, completely factorise the given expression.
Let f(x) = x3 - 7x2 + 14x - 8
f(1) = (1)3 - 7(1)2 + 14(1) - 8 = 1 - 7 + 14 - 8 = 0
Hence, (x - 1) is a factor of f(x).
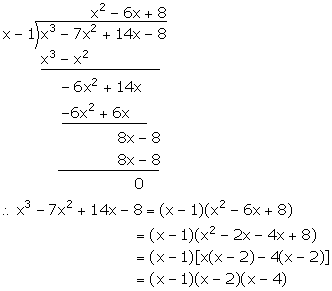
Using Remainder Theorem, factorise:
x3 + 10x2 - 37x + 26 completely
When x3 + 3x2 - mx + 4 is divided by x - 2, the remainder is m + 3. Find the value of m.
Let f(x) = x3 + 3x2 - mx + 4
According to the given information,
f(2) = m + 3
(2)3 + 3(2)2 - m(2) + 4 = m + 3
8 + 12 - 2m + 4 = m + 3
24 - 3 = m + 2m
3m = 21
m = 7
Let the required number be k.
Let f(x) = 3x3 - 8x2 + 4x - 3 - k
According to the given information,
f (-2) = 0
3(-2)3 - 8(-2)2 + 4(-2) - 3 - k = 0
-24 - 32 - 8 - 3 - k = 0
-67 - k = 0
k = -67
Thus, the required number is -67.
If (x + 1) and (x - 2) are factors of x3 + (a + 1)x2 - (b - 2)x - 6, find the values of a and b. And then, factorise the given expression completely.
Let f(x) = x3 + (a + 1)x2 - (b - 2)x - 6
Since, (x + 1) is a factor of f(x).
Remainder = f(-1) = 0
(-1)3 + (a + 1)(-1)2 - (b - 2) (-1) - 6 = 0
-1 + (a + 1) + (b - 2) - 6 = 0
a + b - 8 = 0 ...(i)
Since, (x - 2) is a factor of f(x).
Remainder = f(2) = 0
(2)3 + (a + 1) (2)2 - (b - 2) (2) - 6 = 0
8 + 4a + 4 - 2b + 4 - 6 = 0
4a - 2b + 10 = 0
2a - b + 5 = 0 ...(ii)
Adding (i) and (ii), we get,
3a - 3 = 0
a = 1
Substituting the value of a in (i), we get,
1 + b - 8 = 0
b = 7
f(x) = x3 + 2x2 - 5x - 6
Now, (x + 1) and (x - 2) are factors of f(x). Hence, (x + 1) (x - 2) = x2 - x - 2 is a factor of f(x).
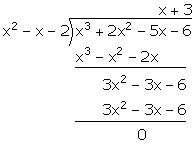
f(x) = x3 + 2x2 - 5x - 6 = (x + 1) (x - 2) (x + 3)
If x - 2 is a factor of x2 + ax + b and a + b = 1, find the values of a and b.
Let f(x) = x2 + ax + b
Since, (x - 2) is a factor of f(x).
Remainder = f(2) = 0
(2)2 + a(2) + b = 0
4 + 2a + b = 0
2a + b = -4 ...(i)
It is given that:
a + b = 1 ...(ii)
Subtracting (ii) from (i), we get,
a = -5
Substituting the value of a in (ii), we get,
b = 1 - (-5) = 6
Factorise x3 + 6x2 + 11x + 6 completely using factor theorem.
Let f(x) = x3 + 6x2 + 11x + 6
For x = -1
f(-1) = (-1)3 + 6(-1)2 + 11(-1) + 6
= -1 + 6 - 11 + 6 = 12 - 12 = 0
Hence, (x + 1) is a factor of f(x).
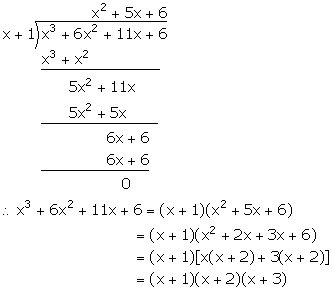
Find the value of 'm', if mx3 + 2x2 - 3 and x2 - mx + 4 leave the same remainder when each is divided by x - 2.
Let f(x) = mx3 + 2x2 - 3
g(x) = x2 - mx + 4
It is given that f(x) and g(x) leave the same remainder when divided by (x - 2). Therefore, we have:
f (2) = g (2)
m(2)3 + 2(2)2 - 3 = (2)2 - m(2) + 4
8m + 8 - 3 = 4 - 2m + 4
10m = 3
m = 
The polynomial px3 + 4x2 - 3x + q is completely divisible by x2 - 1; find the values of p and q. Also, for these values of p and q factorize the given polynomial completely.
Let f(x) = px3 + 4x2 - 3x + q
It is given that f(x) is completely divisible by (x2 - 1) = (x + 1)(x - 1).
Therefore, f(1) = 0 and f(-1) = 0
f(1) = p(1)3 + 4(1)2 - 3(1) + q = 0
p + q + 1 = 0 ...(i)
f(-1) = p(-1)3 + 4(-1)2 - 3(-1) + q = 0
-p + q + 7 = 0 ...(ii)
Adding (i) and (ii), we get,
2q + 8 = 0
q = -4
Substituting the value of q in (i), we get,
p = -q - 1 = 4 - 1 = 3
f(x) = 3x3 + 4x2 - 3x - 4
Given that f(x) is completely divisible by (x2 - 1).
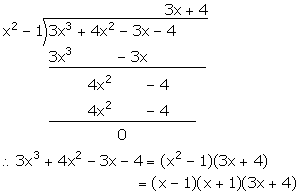
Let the required number be k.
Let f(x) = x2 + x + 3 + k
It is given that f(x) is divisible by (x + 3).
Remainder = 0
f (-3) = 0
(-3)2 + (-3) + 3 + k = 0
9 - 3 + 3 + k = 0
9 + k = 0
k = -9
Thus, the required number is -9.
When the polynomial x3 + 2x2 - 5ax - 7 is divided by (x - 1), the remainder is A and when the polynomial x3 + ax2 - 12x + 16 is divided by (x + 2), the remainder is B. Find the value of 'a' if 2A + B = 0.
It is given that when the polynomial x3 + 2x2 - 5ax - 7 is divided by (x - 1), the remainder is A.
(1)3 + 2(1)2 - 5a(1) - 7 = A
1 + 2 - 5a - 7 = A
- 5a - 4 = A ...(i)
It is also given that when the polynomial x3 + ax2 - 12x + 16 is divided by (x + 2), the remainder is B.
x3 + ax2 - 12x + 16 = B
(-2)3 + a(-2)2 - 12(-2) + 16 = B
-8 + 4a + 24 + 16 = B
4a + 32 = B ...(ii)
It is also given that 2A + B = 0
Using (i) and (ii), we get,
2(-5a - 4) + 4a + 32 = 0
-10a - 8 + 4a + 32 = 0
-6a + 24 = 0
6a = 24
a = 4
(3x + 5) is a factor of the polynomial (a - 1)x3 + (a + 1)x2 - (2a + 1)x - 15. Find the value of 'a', factorise the given polynomial completely.
Let f(x) = (a - 1)x3 + (a + 1)x2 - (2a + 1)x - 15
It is given that (3x + 5) is a factor of f(x).
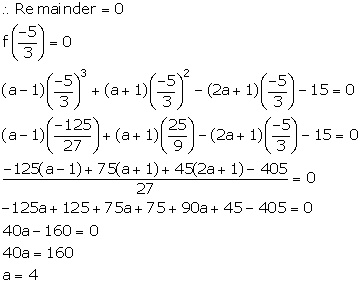
f(x) = (a - 1)x3 + (a + 1)x2 - (2a + 1)x - 15
= 3x3 + 5x2 - 9x - 15
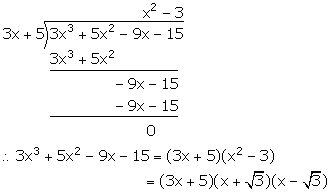
When divided by x - 3 the polynomials x3 - px2 + x + 6 and 2x3 - x2 - (p + 3) x - 6 leave the same remainder. Find the value of 'p'.
If (x - 3) divides f(x) = x3 - px2 + x + 6, then,
Remainder = f(3) = 33 - p(3)2 + 3 + 6 = 36 - 9p
If (x - 3) divides g(x) = 2x3 - x2 - (p + 3) x - 6, then
Remainder = g(3) = 2(3)3 - (3)2 - (p + 3) (3) - 6 = 30 - 3p
Now, f(3) = g(3)
36 - 9p = 30 - 3p
-6p = -6
p = 1
Use the Remainder Theorem to factorise the following expression:
2x3 + x2 - 13x + 6
f(x) = 2x3 + x2 - 13x + 6
Factors of constant term 6 are 
1, 2, 3, 6.
Putting x = 2, we have:
f(2) = 2(2)3 + 22 - 13 (2) + 6 = 16 + 4 - 26 + 6 = 0
Hence (x - 2) is a factor of f(x).
Using remainder theorem, find the value of k if on dividing 2x3 + 3x2 - kx + 5 by x - 2, leaves a remainder 7.
Let f(x) = 2x3 + 3x2 - kx + 5
Using Remainder Theorem, we have
f(2) = 7
∴ 2(2)3 + 3(2)2 - k(2) + 5 = 7
∴ 16 + 12 - 2k + 5 = 7
∴ 33 - 2k = 7
∴ 2k = 26
∴ k = 13
Question 16
What must be subtracted from 16x3 - 8x2 + 4x + 7 so that the resulting expression has 2x + 1 as a factor?
Here, f(x) = 16x3 - 8x2 + 4x + 7
Let the number subtracted be k from the given polynomial f(x).
Given that 2x + 1 is a factor of f(x).
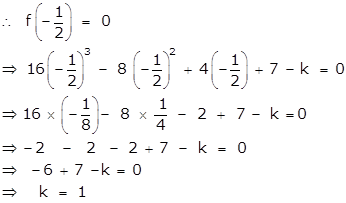
Therefore 1 must be subtracted from 16x3 - 8x2 + 4x + 7 so that the resulting expression has 2x + 1 as a factor.
No comments:
Post a Comment