Evaluate: if possible:


The number of columns in the first matrix is not equal to the number of rows in the second matrix. Thus, the product is not possible.
If ![]() and I is a unit matrix of order 2
and I is a unit matrix of order 2 ![]() 2, find:
2, find:
(i) AB (ii) BA (iii) AI
(iv) IB (v) A2 (vi) B2A


'
Find x and y, if:
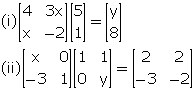
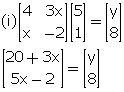
Comparing the corresponding elements, we get,
5x - 2 = 8 ![]() x = 2
x = 2
20 + 3x = y ![]() y = 20 + 6 = 26
y = 20 + 6 = 26
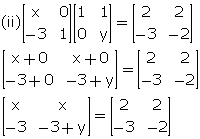
Comparing the corresponding elements, we get,
x = 2
-3 + y = -2 ![]() y = 1
y = 1
If ![]() , find:
, find:
(i) (AB)C (ii) A(BC)
Is A(BC) = (AB)C?
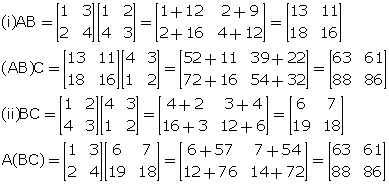
Hence, A(BC) = (AB)C
Given 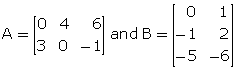 , find; if possible:
, find; if possible:
(i) AB (ii) BA (iii)A2
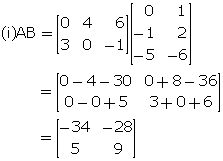

(iii) Product AA (=A2) is not possible as the number of columns of matrix A is not equal to its number of rows.
If M = ![]() and I is a unit matrix of the same order as that of M; show that:
and I is a unit matrix of the same order as that of M; show that:
M2 = 2M + 3I
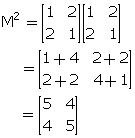
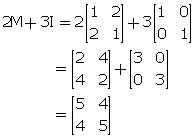
Hence, M2 = 2M + 3I.
If ![]() and BA= M2, find the values of a and b.
and BA= M2, find the values of a and b.
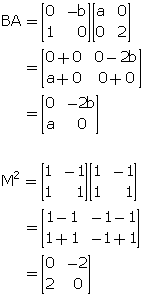
Given, BA = M2
![]()
Comparing the corresponding elements, we get,
a = 2 and -2b = -2 ![]() b = 1
b = 1
Given ![]() , find:
, find:
(i) A - B (ii) A2
(iii) AB (iv) A2 - AB + 2B
![]()
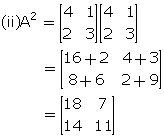
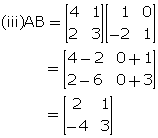

If ![]() ; find:
; find:
(i) (A + B)2 (ii) A2 + B2
(iii) Is (A + B)2 = A2 + B2?
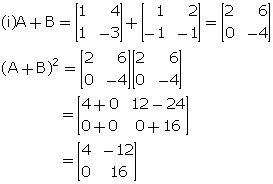
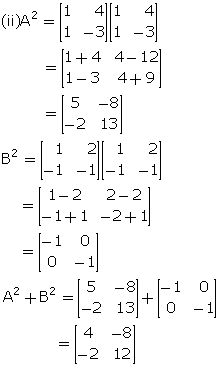
(iii) Clearly, (A + B)2 ![]() A2 + B2
A2 + B2
Find the matrix A, if B =![]() and B2 = B +
and B2 = B + ![]() A.
A.
B2 = B + ![]() A
A
![]() A = B2 - B
A = B2 - B
A = 2(B2 - B)
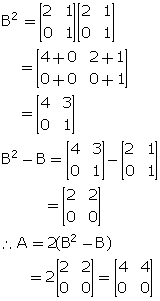
If A = ![]() and A2 = I; find a and b.
and A2 = I; find a and b.
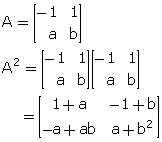
It is given that A2 = I.
![]()
Comparing the corresponding elements, we get,
1 + a = 1
Therefore, a = 0
-1 + b = 0
Therfore, b = 1
If ![]() ; then show that:
; then show that:
(i) A (B + C) = AB + AC
(ii) (B - A)C = BC - AC.


If ![]() , simplify:
, simplify:
A2 + BC.

Solve for x and y:
Solve for x and y:
In each case given below, find:
(a) The order of matrix M.
(b) The matrix M.

We know, the product of two matrices is defined only when the number of columns of first matrix is equal to the number of rows of the second matrix.
(i) Let the order of matrix M be a x b.
![]()
Clearly, the order of matrix M is 1 x 2.

Comparing the corresponding elements, we get,
a = 1 and a + 2b = 2 ![]() 2b = 2 - 1 = 1
2b = 2 - 1 = 1 ![]() b =
b = ![]()
![]()
(ii) Let the order of matrix M be a x b.
![]()
Clearly, the order of matrix M is 2 x 1.
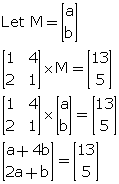
Comparing the corresponding elements, we get,
a + 4b = 13 ....(1)
2a + b = 5 ....(2)
Multiplying (2) by 4, we get,
8a + 4b = 20 ....(3)
Subtracting (1) from (3), we get,
7a = 7 ![]() a = 1
a = 1
From (2), we get,
b = 5 - 2a = 5 - 2 = 3
![]()
If ![]() ; find the value of x, given that: A2 = B.
; find the value of x, given that: A2 = B.

If A and B are any two 2 x 2 matrices such that AB = BA = B and B is not a zero matrix, what can you say about the matrix A?
AB = BA = B
We know that I × B = B × I = B, where I is the identity matrix.
Hence, A is an identity matrix.
Given ![]() and that AB = A + B; find the values of a, b and c.
and that AB = A + B; find the values of a, b and c.
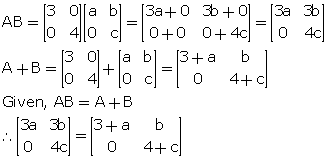
Comparing the corresponding elements, we get,
3a = 3 + a
![]() 2a = 3
2a = 3
![]() a =
a = ![]()
3b = b ![]() b = 0
b = 0
4c = 4 + c ![]() 3c = 4
3c = 4 ![]() c =
c = ![]()
If ![]() , then compute:
, then compute:
(i) P2 - Q2 (ii) (P + Q) (P - Q)
Is (P + Q) (P - Q) = P2 - Q2 true for matrix algebra?

Clearly, it can be said that:
(P + Q) (P - Q) = P2 - Q2 not true for matrix algebra.
Given the matrices:
![]() . Find:
. Find:
(i) ABC (ii) ACB.
State whether ABC = ACB.

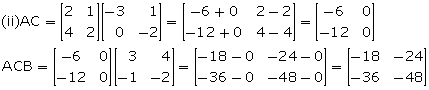
Hence, ABC ≠ ACB.

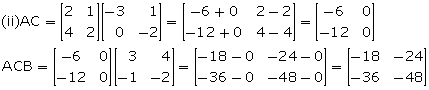
Hence, ABC ≠ ACB.
If ![]() ; find each of the following and state if they are equal:
; find each of the following and state if they are equal:
(i) CA + B (ii) A + CB
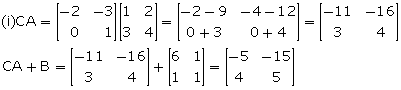
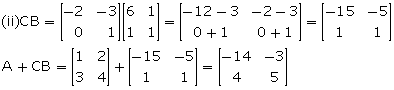
Thus, CA + B ![]() A + CB
A + CB
If ![]() ; find the matrix X such that AX = B.
; find the matrix X such that AX = B.
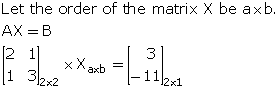
Clearly, the order of matrix X is 2 x 1.

Comparing the two matrices, we get,
2x + y = 3 … (1)
x + 3y = -11 … (2)
Multiplying (1) with 3, we get,
6x + 3y = 9 … (3)
Subtracting (2) from (3), we get,
5x = 20
x = 4
From (1), we have:
y = 3 - 2x = 3 - 8 = -5
![]()
If![]() , find (A - 2I) (A - 3I).
, find (A - 2I) (A - 3I).

If ![]() , find:
, find:
(i) At. A (ii) A. At
Where At is the transpose of matrix A.
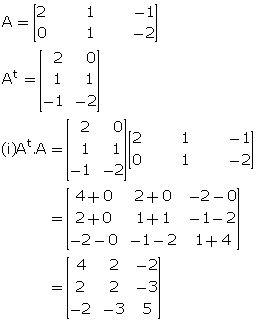
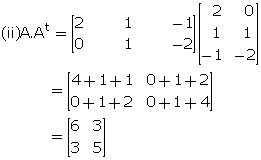
If![]() , show that: 6M - M2 = 9I; where I is a 2 x 2 unit matrix.
, show that: 6M - M2 = 9I; where I is a 2 x 2 unit matrix.
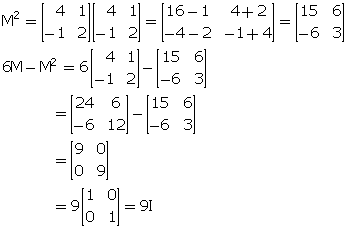
Hence, proved.
If![]() ; find x and y such that PQ = null matrix.
; find x and y such that PQ = null matrix.

Comparing the corresponding elements, we get,
2x + 12 = 0
thus, x = -6
6 + 6y = 0
thus, y = -1
Evaluate without using tables:
![]()

State, with reason, whether the following are true or false. A, B and C are matrices of order 2 x 2.
(i) A + B = B + A
(ii) A - B = B - A
(iii) (B. C). A = B. (C. A)
(iv) (A + B). C = A. C + B. C
(v) A. (B - C) = A. B - A. C
(vi) (A - B). C = A. C - B. C
(vii) A2 - B2 = (A + B) (A - B)
(viii) (A - B)2 = A2 - 2A. B + B2
(i) True.
Addition of matrices is commutative.
(ii) False.
Subtraction of matrices is not commutative.
(iii) True.
Multiplication of matrices is associative.
(iv) True.
Multiplication of matrices is distributive over addition.
(v) True.
Multiplication of matrices is distributive over subtraction.
(vi) True.
Multiplication of matrices is distributive over subtraction.
(vii) False.
Laws of algebra for factorization and expansion are not applicable to matrices.
(viii) False.
Laws of algebra for factorization and expansion are not applicable to matrices.
No comments:
Post a Comment