Chapter 10 - Arithmetic Progression Exercise Ex. 10(A)

Question 1

Which of the following sequences are in arithmetic progression?

(i) 2, 6, 10, 14,

(ii) 15, 12, 9, 6,

(iii) 5, 9, 12, 18,

(iv) 

Solution 1

Question 2

The n^th term of sequence is (2n - 3), find its fifteenth term.

Solution 2

Question 3

If the p^th term of an A.P. is (2p + 3), find the A.P.

Solution 3

Question 4

Find the 24^th term of the sequence:

12, 10, 8, 6,……

Solution 4

Question 5

Find the 30^th term of the sequence:

Solution 5

Question 6

Solution 6

Question 7

Solution 7

Question 8

Is 402 a term of the sequence :

8, 13, 18, 23,………….?

Solution 8

Question 9

Solution 9

Question 10

How many terms are there in the series :

(i) 4, 7, 10, 13, …………, 148?

(ii) 0.5, 0.53, 0.56, ……………, 1.1?

Solution 10

 

Question 11

Which term of the A.P. 1, 4, 7, 10, ………. is 52?

Solution 11

The given A.P. is 1, 4, 7, 10, ………. 

Question 12

If 5^th and 6^th terms of an A.P are respectively 6 and 5. Find the 11^th term of the A.P

Solution 12

Question 13

If t_n represents n^th term of an A.P, t₂ + t₅ - t₃ = 10 and t₂ + t₉ = 17, find its first term and its common difference.

Solution 13

Question 14

Find the 10^th term from the end of the A.P. 4, 9, 14,…….., 254

Solution 14

Question 15

Determine the arithmetic progression whose 3^rd term is 5 and 7^th term is 9.

Solution 15

Question 16

Find the 31^st term of an A.P whose 10^th term is 38 and 16^th term is 74.

Solution 16

Question 17

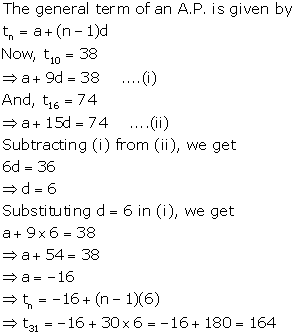
Which term of the series :

21, 18, 15, …………. is - 81?

Can any term of this series be zero? If yes find the number of term.

Solution 17

Question 18

An A.P. consists of 60 terms, If the first and the last terms be 7 and 125 respectively, find the 31^st term.

Solution 18

For a given A.P.,

Number of terms, n = 60

First term, a = 7

Last term, l = 125

⇒ t₆₀ = 125

⇒ a + 59d = 125

⇒ 7 + 59d = 125

⇒ 59d = 118

⇒ d = 2

Hence, t₃₁ = a + 30d = 7 + 30(2) = 7 + 60 = 67

Question 19

The sum of the 4^th and the 8^th terms of an A.P. is 24 and the sum of the 6^th and the 10^th terms of the same A.P. is 34. Find the first three terms of the A.P.

Solution 19

Let 'a' be the first term and 'd' be the common difference of the given A.P.

t₄ + t₈ = 24 (given)

⇒ (a + 3d) + (a + 7d) = 24

⇒ 2a + 10d = 24

⇒ a + 5d = 12 ….(i)

And,

t₆ + t₁₀ = 34 (given)

⇒ (a + 5d) + (a + 9d) = 34

⇒ 2a + 14d = 34

⇒ a + 7d = 17 ….(ii)

Subtracting (i) from (ii), we get

2d = 5

Question 20

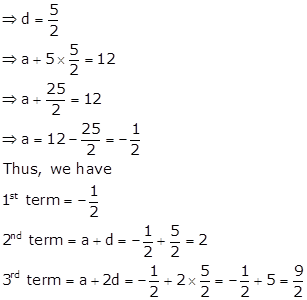
If the third term of an A.P. is 5 and the seventh term is 9, find the 17^th term.

Solution 20

Let 'a' be the first term and 'd' be the common difference of the given A.P.

Now, t₃ = 5 (given)

⇒ a + 2d = 5 ….(i)

And,

t₇ = 9 (given)

⇒ a + 6d = 9 ….(ii)

Subtracting (i) from (ii), we get

4d = 4

⇒ d = 1

⇒ a + 2(1) = 5

⇒ a = 3

Hence, 17^th term = t₁₇ = a + 16d = 3 + 16(1) = 19