Given a triangle ABC in which A = (4, -4), B = (0, 5) and C = (5, 10). A point P lies on BC such that BP: PC = 3: 2. Find the length of line segment AP.
Given, BP: PC = 3: 2
Using section formula, the co-ordinates of point P are

Using distance formula, we have:
![]()
A (20, 0) and B (10, -20) are two fixed points. Find the co-ordinates of a point P in AB such that: 3PB = AB. Also, find the co-ordinates of some other point Q in AB such that AB = 6AQ.
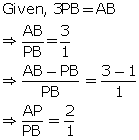
Using section formula,
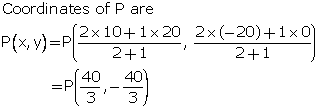
Given, AB = 6AQ

Using section formula,
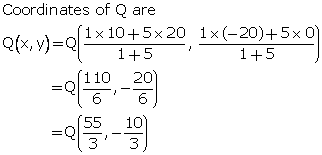
A (-8, 0), B (0, 16) and C (0, 0) are the vertices of a triangle ABC. Point P lies on AB and Q lies on AC such that AP: PB = 3: 5 and AQ: QC = 3: 5. Show that: PQ = ![]() BC.
BC.
Given that, point P lies on AB such that AP: PB = 3: 5.
The co-ordinates of point P are

Also, given that, point Q lies on AB such that AQ: QC = 3: 5.
The co-ordinates of point Q are

Using distance formula,
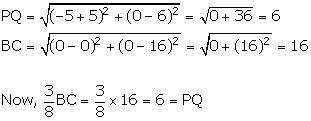
Hence, proved.
Find the co-ordinates of points of trisection of the line segment joining the point (6, -9) and the origin.
Let P and Q be the points of trisection of the line segment joining A (6, -9) and B (0, 0).
P divides AB in the ratio 1: 2. Therefore, the co-ordinates of point P are
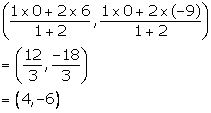
Q divides AB in the ratio 2: 1. Therefore, the co-ordinates of point Q are

Thus, the required points are (4, -6) and (2, -3).
A line segment joining A ![]() and B (a, 5) is divided in the ratio 1: 3 at P, point where the line segment AB intersects the y-axis.
and B (a, 5) is divided in the ratio 1: 3 at P, point where the line segment AB intersects the y-axis.
(i) Calculate the value of 'a'.
(ii) Calculate the co-ordinates of 'P'.
Since, the line segment AB intersects the y-axis at point P, let the co-ordinates of point P be (0, y).
P divides AB in the ratio 1: 3.

Thus, the value of a is 3 and the co-ordinates of point P are![]() .
.
In what ratio is the line joining A (0, 3) and B (4, -1) divided by the x-axis? Write the co-ordinates of the point where AB intersects the x-axis.
Let the line segment AB intersects the x-axis by point P (x, 0) in the ratio k: 1.
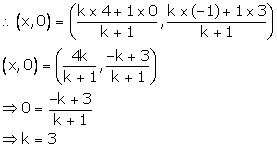
Thus, the required ratio in which P divides AB is 3: 1.
Also, we have:
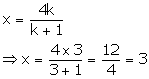
Thus, the co-ordinates of point P are (3, 0).
The mid-point of the segment AB, as shown in diagram, is C (4, -3). Write down the co-ordinates of A and B.
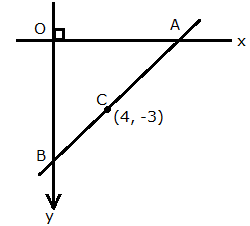
Since, point A lies on x-axis, let the co-ordinates of point A be (x, 0).
Since, point B lies on y-axis, let the co-ordinates of point B be (0, y).
Given, mid-point of AB is C (4, -3).
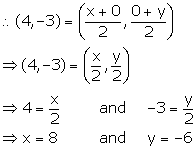
Thus, the co-ordinates of point A are (8, 0) and the co-ordinates of point B are (0, -6).
AB is a diameter of a circle with centre C = (-2, 5). If A = (3, -7), find
(i) the length of radius AC
(ii) the coordinates of B.
![]()

Find the co-ordinates of the centroid of a triangle ABC whose vertices are:
A (-1, 3), B (1, -1) and C (5, 1)
Co- ordinates of the centroid of triangle ABC are
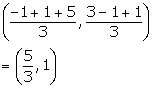
The mid-point of the line-segment joining (4a, 2b - 3) and (-4, 3b) is (2, -2a). Find the values of a and b.
It is given that the mid-point of the line-segment joining (4a, 2b - 3) and (-4, 3b) is (2, -2a).
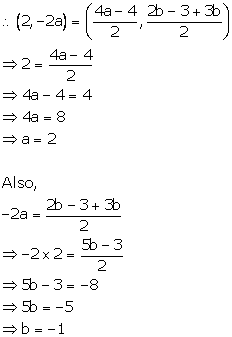
The mid-point of the line segment joining (2a, 4) and (-2, 2b) is (1, 2a + 1). Find the value of a and b.
Mid-point of (2a, 4) and (-2, 2b) is (1, 2a + 1), therefore using mid-point formula, we have:
![]() y =
y = ![]()
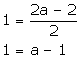 2a + 1 =
2a + 1 = ![]()
![]() a = 2
a = 2 ![]()
Putting, a = 2 in 2a + 1 = 2 + b, we get,
5 - 2 = b ![]() b = 3
b = 3
Therefore, a = 2, b = 3.
(i) Write down the co-ordinates of the point P that divides the line joining A (-4, 1) and B (17, 10) in the ratio 1: 2.
(ii) Calculate the distance OP, where O is the origin.
(iii) In what ratio does the y-axis divide the line AB?
(i) Co-ordinates of point P are

(ii) OP = ![]()
(iii) Let AB be divided by the point P (0, y) lying on y-axis in the ratio k: 1.

Thus, the ratio in which the y-axis divide the line AB is 4: 17.
Prove that the points A (-5, 4), B (-1, -2) and C (5, 2) are the vertices of an isosceles right-angled triangle. Find the co-ordinates of D so that ABCD is a square.
We have:
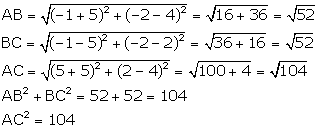
![]() AB = BC and
AB = BC and ![]()
![]() ABC is an isosceles right-angled triangle.
ABC is an isosceles right-angled triangle.
Let the coordinates of D be (x, y).
If ABCD is a square, then,
Mid-point of AC = Mid-point of BD
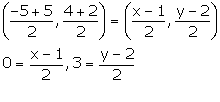
x = 1, y = 8
Thus, the co-ordinates of point D are (1, 8).
M is the mid-point of the line segment joining the points A (-3, 7) and B (9, -1). Find the co-ordinates of point M. Further, if R (2, 2) divides the line segment joining M and the origin in the ratio p: q, find the ratio p: q.
Given, M is the mid-point of the line segment joining the points A (-3, 7) and B (9, -1).
The co-ordinates of point M are

Also, given that, R (2, 2) divides the line segment joining M and the origin in the ratio p: q.

Thus, the ratio p: q is 1: 2.
Calculate the ratio in which the line joining A(-4, 2) and B(3, 6) is divided by point P(x, 3). Also, find
- x
- length of AP.
Find the ratio in which the line 2x + y = 4 divides the line segment joining the points P(2, -2) and Q(3, 7).

If the abscissa of a point P is 2. Find the ratio in which this point divides the line segment joining the point (-4, 3) and (6, 3). Al so, find the co-ordinates of point P.
The line joining the points (2, 1) and (5, -8) is trisected at the points P and Q, point P lies on the line 2x - y + k = 0, find the value of k. Also, find the co-ordinates of point Q.
Find the image of the point A(5, -3), under reflection in the point P(-1, 3).
Let A' = (x, y) be the image of the point A(5, -3), under reflection in the point P(-1, 3).
⇒ P(-1, 3) is the mid - point of the line segment AA'.
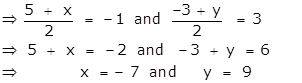
Therefore the image of the point A(5, -3), under reflection in the point P(-1, 3) is A'(-7, 9).
M is the mid-point of the line segment joining the points A(0, 4) and B(6, 0). M also divides the line segment OP in the ratio 1 : 3. Find :
- co-ordinates of M
- co-ordinates of P
- length of BP
A(-4, 2), B(0, 2) and C(-2, -4) are the vertices of a triangle ABC. P, Q and R are mid-points of sides BC, CA and AB respectively. Show that the centroid of ∆ PQR is the same as the centroid of ∆ ABC.

No comments:
Post a Comment