Chapter 20 - Cylinder, Cone and Sphere (Surface Area and Volume) Exercise Ex. 20(A)

Question 1

The height of a circular cylinder is 20 cm and the radius of its base is 7 cm. Find :

(i) the volume

(ii) the total surface area.

Solution 1

Question 2

The inner radius of a pipe is 2.1 cm. How much water can 12 m of this pipe hold?

Solution 2

Inner radius of pipe = 2.1 cm

Length of the pipe = 12 m = 1200 cm

Question 3

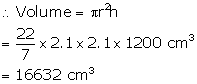
A cylinder of circumference 8 cm and length 21 cm rolls without sliding for seconds at the rate of 9 complete rounds per second. Find

(i) distance travelled by the cylinder in seconds, and

(ii) the area covered by the cylinder in seconds

Solution 3

Circumference of cylinder = 8 cm

Therefore, radius = 

Length of the cylinder (h)= 21 cm

(i) If distance covered in one revolution is 8 cm, then distance covered in 9 revolutions = 9  8 = 72 cm or distance covered in 1 second = 72 cm.

Therefore, distance covered in seconds = 

(ii) Curved surface area = 

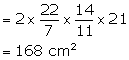
Area covered in one revolution = 

Area covered in 9 revolutions = 

Therefore, area covered in 1 second = 

Hence, area covered in seconds = 

Question 4

How many cubic meters of earth must be dug out to make a well 28 m deep and 2.8 m in diameter? Also, find the cost of plastering its inner surface at Rs 4.50 per sq meter.

Solution 4

Radius of the well = 

Depth of the well = 28 m

Therefore, volume of earth dug out = 

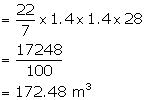
Area of curved surface = 

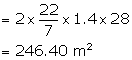
Cost of plastering at the rate of Rs 4.50 per sq m

= Rs 246.40  4.50

= Rs 1108.80

Question 5

What length of solid cylinder 2 cm in diameter must be taken to recast into a hollow cylinder of external diameter 20 cm, 0.25 cm thick and 15 cm long?

Solution 5

External diameter of hollow cylinder = 20 cm

Therefore, radius = 10 cm

Thickness = 0.25 cm

Hence, internal radius = (10 - 0.25) = 9.75 cm

Length of cylinder (h) = 15 cm

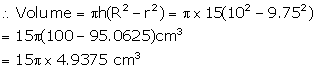
Diameter = 2 cm

Therefore, radius (r) = 1 cm

Let h be the length

then, 

Now, according to given condition:

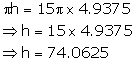
Length of cylinder = 74.0625 cm

Question 6

A cylinder has a diameter of 20 cm. The area of curved surface is 100 sq cm. Find:

(i) the height of the cylinder correct to one decimal place.

(ii) the volume of the cylinder correct to one decimal place.

Solution 6

Diameter of the cylinder = 20 cm

Hence, Radius (r) = 10 cm

Height = h cm

(i) Curved surface area = 

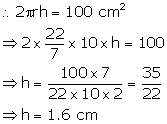
(ii) Volume of the cylinder = 

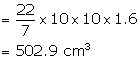
or

Question 7

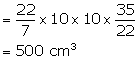
A metal pipe has a bore (inner diameter) of 5 cm. The pipe is 5 mm thick all round. Find the weight, in kilogram, of 2 metres of the pipe if 1 cm³ of the metal weights 7.7 g.

Solution 7

Question 8

A cylindrical container with diameter of base 42 cm contains sufficient water to submerge a rectangular solid of iron with dimensions 22 cm x 14 cm  10.5 cm. Find the rise in level of the water when the solid is submerged.

Solution 8

Diameter of cylindrical container = 42 cm

Therefore, radius (r) = 21 cm

Dimensions of rectangular solid = 22cm  14cm  10.5cm

Volume of solid = 

Let height of water = h

Therefore, volume of water in the container = 

 

From (i) and (ii)

Question 9

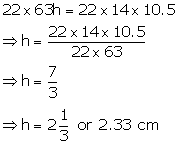
A cylindrical container with internal radius of its base 10 cm, contains water up to a height of 7 cm. Find the area of wetted surface of the cylinder.

Solution 9

Internal radius of the cylindrical container = 10 cm

Height of water = 7 cm

Therefore, surface area of the wetted surface =

Question 10

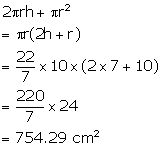
Find the total surface area of an open pipe of length 50 cm, external diameter 20 cm and internal diameter 6 cm.

Solution 10

Length of an open pipe = 50 cm

External diameter = 20 cm  External radius (R) = 10 cm

Internal diameter = 6 cm  Internal radius (r) = 3 cm

Surface area of pipe open from both sides =

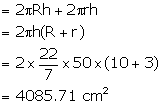
Area of upper and lower part =

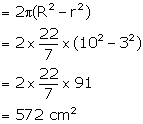
Total surface area = 

Question 11

The height and radius of base of a cylinder are in the ratio 3:1. If its volume is find its total surface area.

Solution 11

Ratio between height and radius of a cylinder = 3:1

Volume =  …….(i)

Let radius of the base = r

then height = 3r

from (i) and (ii)

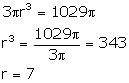
Therefore, radius = 7 cm and height = 3 x 7 = 21 cm

Now, total surface area =

Question 12

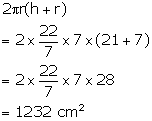
The radius of a solid right circular cylinder increases by 20% and its height decreases by 20%. Find the percentage change in its volume.

Solution 12

Question 13

The radius of a solid right circular cylinder decreases by 20% and its height increases by 10%. Find the percentage change in its :

(i) volume (ii) curved surface area

Solution 13

Question 14

Find the minimum length in cm and correct to nearest whole number of the thin metal sheet required to make a hollow and closed cylindrical box of diameter 20 cm and height 35 cm. Given that the width of the metal sheet is 1 m. Also, find the cost of the sheet at the rate of Rs. 56 per m.

Find the area of metal sheet required, if 10% of it is wasted in cutting, overlapping, etc.

Solution 14

Question 15

3080 cm3 of water is required to fill a cylindrical vessel completely and 2310 cm³ of water is required to fill it upto 5 cm below the top. Find :

(i) radius of the vessel.

(ii) height of the vessel.

(iii) wetted surface area of the vessel when it is half-filled with water.

Solution 15

Question 16

Find the volume of the largest cylinder formed when a rectangular piece of paper 44 cm by 33 cm is rolled along it :

(i) shorter side. (ii) longer side.

Solution 16

Question 17

A metal cube of side 11 cm is completely submerged in water contained in a cylindrical vessel with diameter 28 cm. Find the rise in the level of water.

Solution 17

Question 18

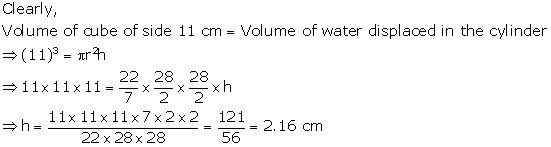
A circular tank of diameter 2 m is dug and the earth removed is spread uniformly all around the tank to form an embankment 2 m in width and 1.6 m in height. Find the depth of the circular tank.

Solution 18

Question 19

The sum of the inner and the outer curved surfaces of a hollow metallic cylinder is 1056 cm² and the volume of material in it is 1056 cm³. Find its internal and external radii. Given that the height of the cylinder is 21 cm.

Solution 19

Question 20

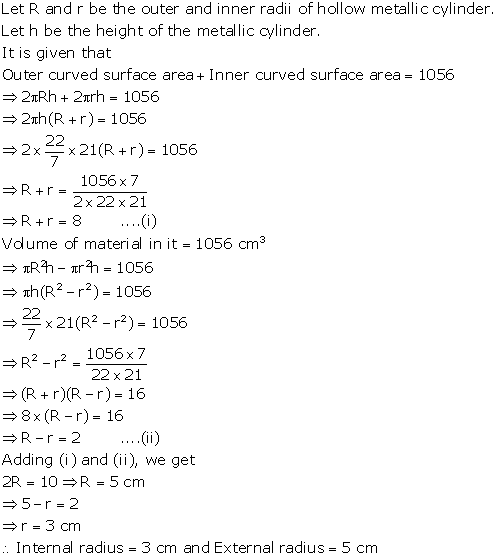
The difference between the outer curved surface area and the inner curved surface area of a hollow cylinder is 352 cm². If its height is 28 cm and the volume of material in it is 704 cm³;find its external curved surface area.

Solution 20

Question 21

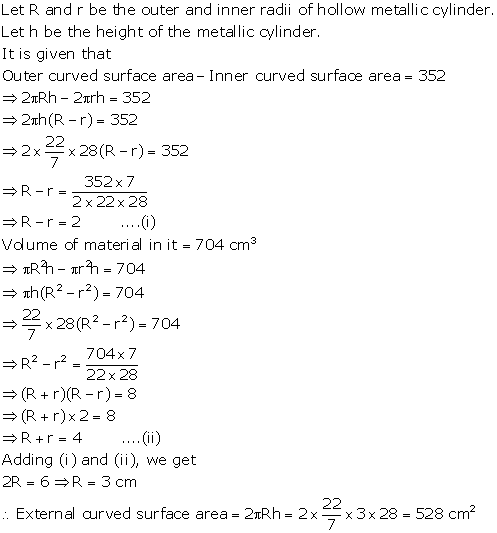
The sum of the heights and the radius of a solid cylinder is 35 cm and its total surface area is 3080 cm², find the volume of the cylinder.

Solution 21

Question 22

The total surface area of a solid cylinder is 616 cm². If the ratio between its curved surface area and total surface area is 1 : 2; find the volume of the cylinder.

Solution 22

Question 23

A cylindrical vessel of height 24 cm and diameter 40 cm is full of water. Find the exact number of small cylindrical bottles, each of height 10 cm and diameter 8 cm, which can be filled with this water.

Solution 23

Question 24

Two solid cylinders, one with diameter 60 cm and height 30 cm and the other with radius 30 cm and height 60 cm, are metled and recasted into a third solid cylinder of height 10 cm. Find the diameter of the cylinder formed.

Solution 24

Question 25

The total surface area of a hollow cylinder, which is open from both sides, is 3575 cm²; area of the base ring is 357.5 cm² and height is 14 cm. Find the thickness of the cylinder.

Solution 25

Total surface area of a hollow cylinder = 3575 cm²

Area of the base ring = 357.5 cm²

Height = 14 cm

Let external radius = R and internal radius = r

Let thickness of the cylinder = d = (R-r)

Therefore, Total surface area = 

and Area of base =

Dividing (i) by (ii)

Hence, thickness of the cylinder = 3.5 cm

Question 26

 

 

The given figure shows a solid formed of a solid cube of side 40cm and a solid cylinder of radius 20 cm and height 50 cm attached to the cube as shown.

Find the volume and the total surface area of the whole solid (Take π = 3.14)

Solution 26

Question 27

Two right circular solid cylinders have radii in the ratio 3 : 5 and heights in the ratio 2 : 3, Find the ratio between their :

(i) curved surface areas.

(ii) volumes.

Solution 27

Question 28

Solution 28