A solid sphere of radius 15 cm is melted and recast into solid right circular cones of radius 2.5 cm and height 8 cm. Calculate the number of cones recast.

A hollow sphere of internal and external diameters 4 cm and 8 cm respectively is melted into a cone of base diameter 8 cm. Find the height of the cone.
External diameter = 8 cm
Therefore, radius (R) = 4 cm
Internal diameter = 4 cm
Therefore, radius (r) = 2 cm
Volume of metal used in hollow sphere = ![]()
Diameter of cone = 8 cm
Therefore, radius = 4 cm
Let height of cone = h
![]()
From (i) and (ii)
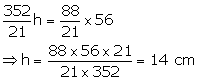
Height of the cone = 14 cm
The radii of the internal and external surfaces of a metallic spherical shell are 3 cm and 5 cm respectively. It is melted and recast into a solid right circular cone of height 32 cm. find the diameter of the base of the cone.
Internal radius = 3cm
External radius = 5 cm
Volume of spherical shell
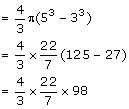
Volume of solid circular cone
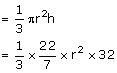
Vol. of Cone = Vol. of sphere
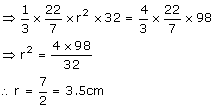
Hence, diameter = 2r = 7 cm
Total volume of three identical cones is the same as that of a bigger cone whose height is 9 cm and diameter 40 cm. find the radius of the base of each smaller cone, if height of each is 108 cm.
Let the radius of the smaller cone be 'r' cm.
Volume of larger cone
![]()
Volume of smaller cone
![]()
Volume of larger cone=3× Volume of smaller cone
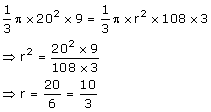
A solid rectangular block of metal 49 cm by 44 cm by 18 cm is melted and formed into a solid sphere. Calculate the radius of the sphere.
Volume of rectangular block = ![]()
Let r be the radius of sphere
![]()
From (i) and (ii)
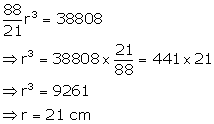
Radius of sphere = 21 cm
A hemi-spherical bowl of internal radius 9 cm is full of liquid. This liquid is to be filled into conical shaped small containers each of diameter 3 cm and height 4 cm. How many containers are necessary to empty the bowl?
Radius of hemispherical bowl = 9 cm
![]()
Diameter each of cylindrical bottle = 3 cm
Radius = ![]() cm, and height = 4 cm
cm, and height = 4 cm
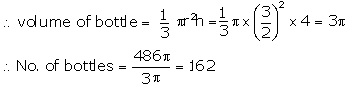
A hemispherical bowl of diameter 7.2 cm is filled completely with chocolate sauce. This sauce is poured into an inverted cone of radius 4.8 cm. Find the height of the cone if it is completely filled.
Diameter of the hemispherical bowl = 7.2 cm
Therefore, radius = 3.6 cm
Volume of sauce in hemispherical bowl = ![]()
Radius of the cone = 4.8 cm
Volume of cone = ![]()
Now, volume of sauce in hemispherical bowl = volume of cone

Height of the cone = 4.05 cm
A solid cone of radius 5 cm and height 8 cm is melted and made into small spheres of radius 0.5 cm. Find the number of spheres formed.
Radius of a solid cone (r) = 5 cm
Height of the cone = 8 cm
![]() Volume of a cone
Volume of a cone
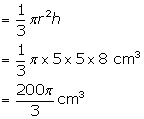

The total area of a solid metallic sphere is 1256 cm2. It is melted and recast into solid right circular cones of radius 2.5 cm and height 8 cm. Calculate:
(i) the radius of the solid sphere
(ii) the number of cones recasted [![]() ]
]
Total area of solid metallic sphere = 1256 cm2
(i)Let radius of the sphere is r then
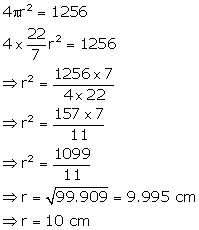
(ii) Volume of sphere = ![]() Volume of right circular cone =
Volume of right circular cone =
![]()
Number of cones
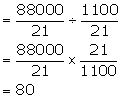
A solid metallic cone, with radius 6 cm and height 10 cm, is made of some heavy metal A. In order to reduce weight, a conical hole is made in the cone as shown and it is completely filled with a lighter metal B. The conical hole has a diameter of 6 cm and depth 4 cm. Calculate the ratio of the volume of the metal A to the volume of metal B in the solid.

Volume of the whole cone of metal A
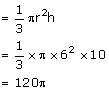
Volume of the cone with metal B
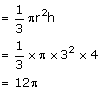
Final Volume of cone with metal A=120 ![]() -12
-12 ![]() =108
=108 ![]()
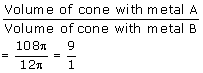
A hollow sphere of internal and external radii 6 cm and 8 cm respectively is melted and recast into small cones of base radius 2 cm and height 8 cm. Find the number of cones.
Let the number of small cones be 'n'
Volume of sphere
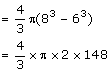
Volume of small spheres
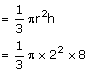
Volume of sphere = n× Volume of small sphere

The number of cones = 37
The surface area of a solid metallic sphere is 2464 cm2. It is melted and recast into solid right circular cones of radius 3.5 cm and height 7 cm. Calculate :
(i) the radius of the sphere.
(ii) the number of cones recast. ![]()

No comments:
Post a Comment