Find the mean of the following set of numbers:
(i) 6, 9, 11, 12 and 7
(ii) 11, 14, 23, 26, 10, 12, 18 and 6
(i)
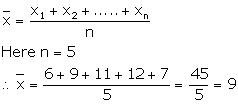
(ii)

Marks obtained (in mathematics) by 9 student are given below:
60, 67, 52, 76, 50, 51, 74, 45 and 56
(a) find the arithmetic mean
(b) if marks of each student be increased by 4; what will be the new value of arithmetic mean.
(a) Here n = 9
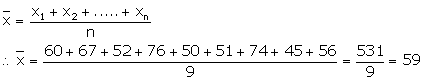
(b)
If marks of each student be increased by 4 then new arithmetic mean will be = 59 + 4 = 63
Find the mean of the natural numbers from 3 to 12.
Numbers between 3 to 12 are 3, 4, 5, 6, 7, 8, 9, 10, 11 and 12.
Here n = 10
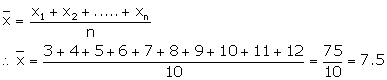
(a) Find the mean of 7, 11, 6, 5, and 6
(b) If each number given in (a) is diminished by 2, find the new value of mean.
(a) The mean of 7, 11, 6, 5 and 6
![]()
(b)
If we subtract 2 from each number, then the mean will be 7-2 = 5
If the mean of 6, 4, 7, 'a' and 10 is 8. Find the value of 'a'
No. of terms = 5
Mean = 8
Sum of numbers = 8 x 5 = 40 .(i)
But, sum of numbers = 6+4+7+a+10 = 27+a ..(ii)
From (i) and (ii)
27+a = 40
a = 13
The mean of the number 6, 'y', 7, 'x' and 14 is 8. Express 'y' in terms of 'x'.
No. of terms = 5 and mean = 8
Sum of numbers = 5 x 8 = 40 ..(i)
but sum of numbers = 6+y+7+x+14 = 27+y+x .(ii)
from (i) and (ii)
27 + y + x = 40
x + y = 13
y = 13 - x
The ages of 40 students are given in the following table:
Age( in yrs) | 12 | 13 | 14 | 15 | 16 | 17 | 18 |
Frequency | 2 | 4 | 6 | 9 | 8 | 7 | 4 |
Find the arithmetic mean.
Age in yrs xi | Frequency (fi) | fixi |
12 | 2 | 24 |
13 | 4 | 52 |
14 | 6 | 84 |
15 | 9 | 135 |
16 | 8 | 128 |
17 | 7 | 119 |
18 | 4 | 72 |
Total | 40 | 614 |
![]()
If 69.5 is the mean of 72, 70, 'x', 62, 50, 71, 90, 64, 58 and 82, find the value of 'x'.
No. of terms = 10
Mean = 69.5
Sum of the numbers = 69.5 x 10 = 695 ..........(i)
But sum of numbers = 72+70+x+62+ 50+71+90+64+58+82
= 619 + x ......(ii)
from (i) and (ii)
619 + x = 695
x = 76
The following table gives the heights of plants in centimeter. If the mean height of plants is 60.95 cm; find the value of 'f'.
Height (cm) | 50 | 55 | 58 | 60 | 65 | 70 | 71 |
No. of plants | 2 | 4 | 10 | f | 5 | 4 | 3 |
Height (cm) xi | No. of Plants fi | fixi |
50 | 2 | 100 |
55 | 4 | 220 |
58 | 10 | 580 |
60 | f | 60f |
65 | 5 | 325 |
70 | 4 | 280 |
71 | 3 | 213 |
Total | 28+f | 1718 + 60f |
Mean = 60.95

From the data given below, calculate the mean wage, correct to the nearest rupee.
Category | A | B | C | D | E | F |
Wages (Rs/day) | 50 | 60 | 70 | 80 | 90 | 100 |
No. of workers | 2 | 4 | 8 | 12 | 10 | 6 |
(i) If the number of workers in each category is doubled, what would be the new mean wage?
(ii) If the wages per day in each category are increased by 60%; what is the new mean wage?
(iii) If the number of workers in each category is doubled and the wages per day per worker are reduced by 40%, what would be the new mean wage?
Wages (Rs/day) (x) | No. of Workers (f) | fx |
50 | 2 | 100 |
60 | 4 | 240 |
70 | 8 | 560 |
80 | 12 | 960 |
90 | 10 | 900 |
100 | 6 | 600 |
Total | 42 | 3360 |
![]()
(i) Mean remains the same if the number of workers in each category is doubled.
Mean = 80
(ii) Mean will be increased by 60% if the wages per day per worker is increased by 60%
New mean = ![]()
(iii) No change in the mean if the number of workers is doubled but if wages per worker is reduced by 40%, then
New mean = ![]()
The contents of 100 match boxes were checked to determine the number of matches they contained.
No. of matches | 35 | 36 | 37 | 38 | 39 | 40 | 41 |
No. of boxes | 6 | 10 | 18 | 25 | 21 | 12 | 8 |
(i) calculate, correct to one decimal place, the mean number of matches per box.
(ii) Determine how many extra matches would have to be added to the total contents of the 100 boxes to bring the mean up to exactly 39 matches.
No. of matches (x) | No. of boxes (f) | fx |
35 | 6 | 210 |
36 | 10 | 360 |
37 | 18 | 666 |
38 | 25 | 950 |
39 | 21 | 819 |
40 | 12 | 480 |
41 | 8 | 328 |
Total | 100 | 3813 |
(i) ![]()
(ii) In the second case,
New mean = 39 matches
Total contents = 39 x 100 = 3900
But total number of matches already given = 3813
Number of new matches to be added = 3900 - 3813 = 87
If the mean of the following distribution is 3, find the value of p.
x | 1 | 2 | 3 | 5 | p + 4 |
f | 9 | 6 | 9 | 3 | 6 |
In the following table, ∑f = 200 and mean = 73. Find the missing frequencies f1, and f2.
x | 0 | 50 | 100 | 150 | 200 | 250 |
f | 46 | f1 | f2 | 25 | 10 | 5 |
Find the arithmetic mean (correct to the nearest whole-number) by using step-deviation method.
x | 5 | 10 | 15 | 20 | 25 | 30 | 35 | 40 | 45 | 50 |
f | 20 | 43 | 75 | 67 | 72 | 45 | 39 | 9 | 8 | 6 |
Find the mean (correct to one place of decimal) by using short-cut method.
x | 40 | 41 | 43 | 45 | 46 | 49 | 50 |
f | 14 | 28 | 38 | 50 | 40 | 20 | 10 |
No comments:
Post a Comment