Prove the following identities:
(i) ![]()
(ii) ![]()
(iii) ![]()
(iv) ![]()
(v) ![]()
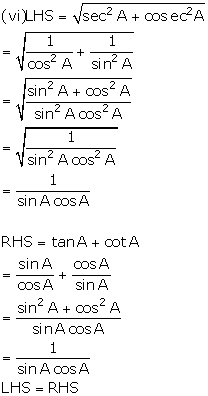
(vi) ![]()
(vii) ![]()
(viii) ![]()
(ix) ![]()
(x) ![]()
(xi) ![]()
(xii) ![]()
(xiii) ![]()
(xiv) ![]()
(xv) ![]()
(xvi) ![]()
(xvii) ![]()
(i) ![]()

(ii)![]()
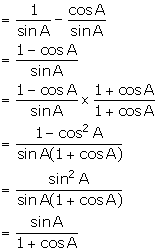
(iii) ![]()
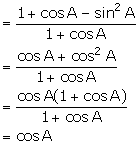
(iv) ![]()
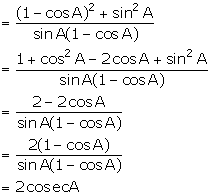
(v) ![]()

(vi) ![]()
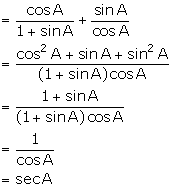
(vii) ![]()

(viii) ![]()

(ix) ![]()
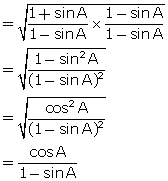
(x) ![]()

(xi)![]()

(xii) ![]()
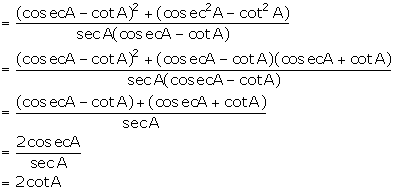
(xiii) ![]()

(xiv) ![]()
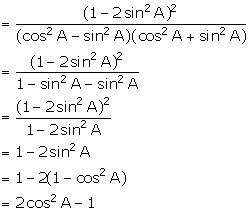
(xv) ![]()
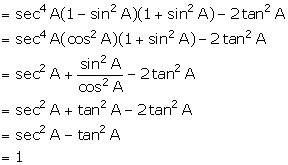
(xvi) ![]()

(xvii) ![]()

If ![]() and
and ![]() , then prove that:
, then prove that:
q(p2 - 1) = 2p

If ![]() , show that:
, show that:
![]()
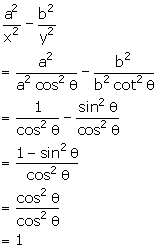
If ![]() , show that:
, show that:
![]()

If tan A = n tan B and sin A = m sin B, prove that:
![]()
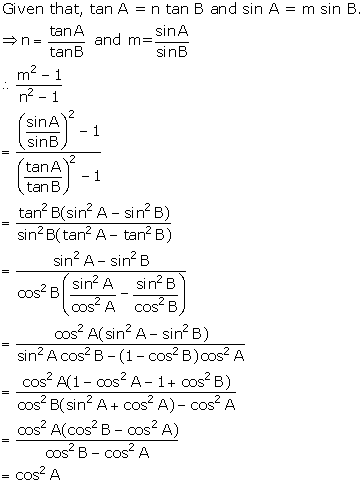
(i) If 2 sinA - 1 = 0, show that:
sin 3A = 3 sinA - 4 sin3A
(ii) If 4 cos2A - 3 = 0, show that:
cos 3A = 4 cos3A - 3 cosA
(i) 2 sinA - 1 = 0
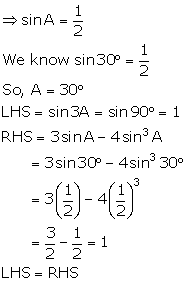
(ii)
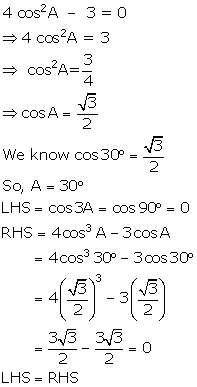
Evaluate:
(i) ![]()
(ii) ![]()
(iii) ![]()
(iv) ![]()
(v) ![]()
(vi) ![]()
(vii) ![]()
(viii) ![]()
(i) ![]()

(ii) ![]()
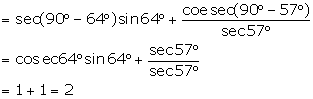
(iii) ![]()
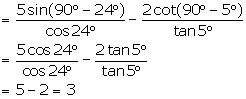
(iv) ![]()
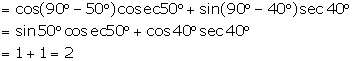
(v) ![]()
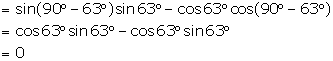
(vi) ![]()

(vii) ![]()
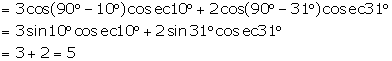
(viii) ![]()
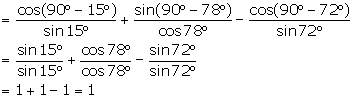
Prove that:
(i) ![]()
(ii) ![]()
(iii) ![]()
(iv) ![]()
(v) ![]()
(i) ![]()
(ii) ![]()
(iii) ![]()
(iv) ![]()
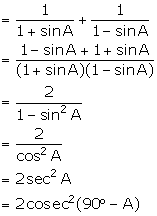
(v) ![]()

If A and B are complementary angles, prove that:
(i) ![]()
(ii) ![]()
(iii) cosec2A + cosec2B = cosec2A cosec2B
(iv) ![]()
Since, A and B are complementary angles, A + B = 90°
(i)

(ii)

(iii)

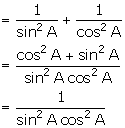
= cosec2A [sec(90 - B)]2
= cosec2A cosec2B
(iv) ![]()
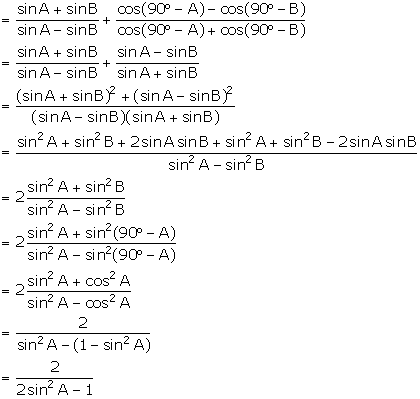
Prove that:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
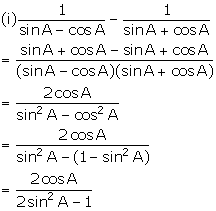

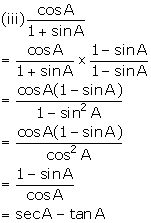
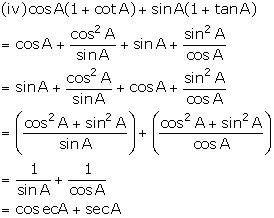


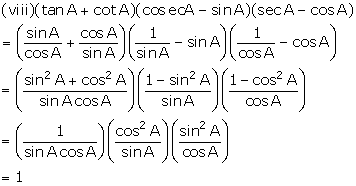
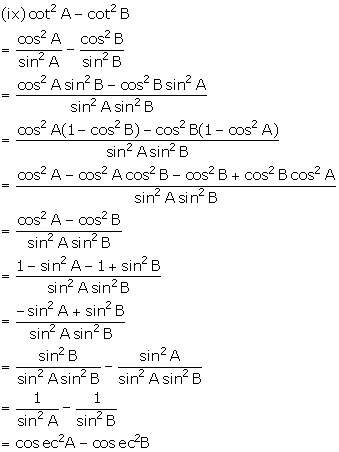

If 4cos2A - 3 = 0 and 0°![]() A
A ![]() 90°, then prove that:
90°, then prove that:
(i) sin3A= 3 sinA - 4 sin3A
(ii) cos3A= 4 cos3A - 3 cosA
4 cos2A - 3 = 0
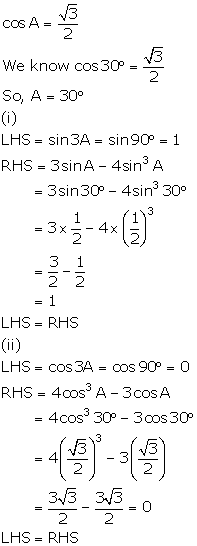
Find A, if 0°![]() A
A ![]() 90° and:
90° and:
(i) ![]()
(ii) sin 3A - 1 = 0
(iii) ![]()
(iv) ![]()
(v) ![]()
(i) ![]()
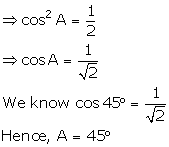
(ii) sin 3A - 1 = 0
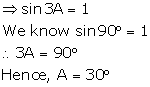
(iii) ![]()
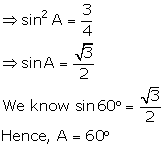
(iv) ![]()
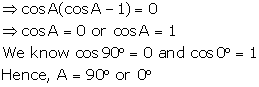
(v) ![]()

If 0° < A < 90°; find A, if:
(i) ![]()
(ii) ![]()
(i) ![]()

(ii) ![]()

Prove that:
(cosec A - sin A) (sec A - cos A) sec2A = tan A
_ASH_files/20141209110714_image002.gif)
Prove the identity (sin θ + cos θ) (tan θ + cot θ) = sec θ + cosec θ.
Evaluate without using trigonometric tables,
sin2 28° + sin2 62° + tan2 38° - cot2 52° + ![]() sec2 30°
sec2 30°
sin2 28° + sin2 62° + tan2 38° - cot2 52° + ![]() sec2 30°
sec2 30°
= sin2 28° + [sin (90 - 28)°]2 + tan2 38° - [cot(90 - 38)°]2 + ![]() sec2 30°
sec2 30°
= sin2 28° + cos2 28° + tan2 38° - tan2 38° + ![]() sec2 30°
sec2 30°
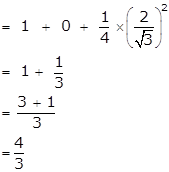
No comments:
Post a Comment