Chapter 7 - Ratio and Proportion (Including Properties and Uses) Exercise Ex. 7(B)

Question 1

Find the fourth proportional to:

(i) 1.5, 4.5 and 3.5 (ii) 3a, 6a² and 2ab²

Solution 1

(i) Let the fourth proportional to 1.5, 4.5 and 3.5 be x.

 1.5 : 4.5 = 3.5 : x

 1.5  x = 3.5  4.5

 x = 10.5

(i) Let the fourth proportional to 3a, 6a² and 2ab² be x.

 3a : 6a² = 2ab² : x

 3a  x = 2ab² 6a²

 3a  x = 12a³b²

 x = 4a²b²

Question 2

Find the third proportional to:

(i) 2 and 4 (ii) a - b and a² - b²

Solution 2

(i) Let the third proportional to 2 and 4 be x.

 2, 4, x are in continued proportion.

 2 : 4 = 4 : x

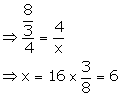
(ii) Let the third proportional to a - b and a² - b² be x.

 a - b, a² - b², x are in continued proportion.

 a - b : a² - b² = a² - b² : x

Question 3

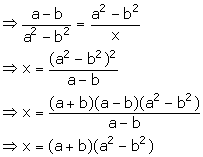
Find the mean proportional between:

(i) 6 + 3 and 8 - 4

(ii) a - b and a³ - a²b

Solution 3

(i) Let the mean proportional between 6 + 3 and 8 - 4 be x.

 6 + 3, x and 8 - 4 are in continued proportion.

 6 + 3 : x = x : 8 - 4

 x x = (6 + 3) (8 - 4)

 x² = 48 + 24- 24 - 36

 x² = 12

 x= 2

 

(ii) Let the mean proportional between a - b and a³ - a²b be x.

 a - b, x, a³ - a²b are in continued proportion.

 a - b : x = x : a³ - a²b

 x x = (a - b) (a³ - a²b)

 x² = (a - b) a²(a - b) = [a(a - b)]²

 x = a(a - b)

Question 4

If x + 5 is the mean proportional between x + 2 and x + 9; find the value of x.

Solution 4

Given, x + 5 is the mean proportional between x + 2 and x + 9.

 (x + 2), (x + 5) and (x + 9) are in continued proportion.

 (x + 2) : (x + 5) = (x + 5) : (x + 9)

 (x + 5)² = (x + 2)(x + 9)

 x² + 25 + 10x = x² + 2x + 9x + 18

 25 - 18 = 11x - 10x

 x = 7

Question 5

If x², 4 and 9 are in continued proportion, find x.

Solution 5

Question 6

What least number must be added to each of the numbers 6, 15, 20 and 43 to make them proportional?

Solution 6

Let the number added be x.

 (6 + x) : (15 + x) :: (20 + x) (43 + x)

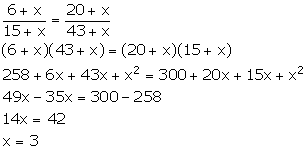
Thus, the required number which should be added is 3.

Question 7(i)

Solution 7(i)

Question 7(ii)

Solution 7(ii)

Question 7(iii)

Solution 7(iii)

Question 8

What least number must be subtracted from each of the numbers 7, 17 and 47 so that the remainders are in continued proportion?

Solution 8

Let the number subtracted be x.

 (7 - x) : (17 - x) :: (17 - x) (47 - x)

Thus, the required number which should be subtracted is 2.

Question 9

If y is the mean proportional between x and z; show that xy + yz is the mean proportional between x²+y² and y²+z².

Solution 9

Since y is the mean proportion between x and z

Therefore, y² = xz

Now, we have to prove that xy+yz is the mean proportional between x²+y² and y²+z², i.e.,

LHS = RHS

Hence, proved.

Question 10

If q is the mean proportional between p and r, show that:

pqr (p + q + r)³ = (pq + qr + rp)³.

Solution 10

Given, q is the mean proportional between p and r.

q² = pr

Question 11

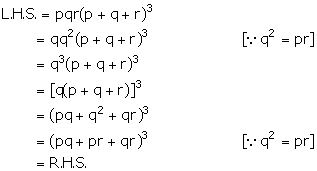
If three quantities are in continued proportion; show that the ratio of the first to the third is the duplicate ratio of the first to the second.

Solution 11

Let x, y and z be the three quantities which are in continued proportion.

Then, x : y :: y : z  y² = xz ....(1)

 

Now, we have to prove that

x : z = x² : y²

That is we need to prove that

xy² = x²z

 

LHS = xy² = x(xz) = x²z = RHS [Using (1)]

Hence, proved.

Question 12

If y is the mean proportional between x and z, prove that:

Solution 12

Given, y is the mean proportional between x and z.

y² = xz

 

Question 13

Given four quantities a, b, c and d are in proportion. Show that:

Solution 13

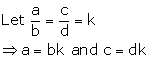
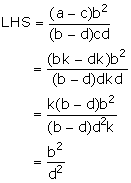
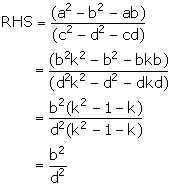
LHS = RHS

Hence proved.

Question 14

Find two numbers such that the mean mean proportional between them is 12 and the third proportional to them is 96.

Solution 14

Let a and b be the two numbers, whose mean proportional is 12.

Now, third proportional is 96

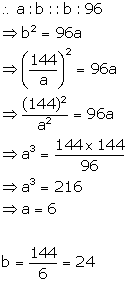
Therefore, the numbers are 6 and 24.

Question 15

Find the third proportional to 

Solution 15

Let the required third proportional be p.

, p are in continued proportion.

Question 16

If p: q = r: s; then show that:

mp + nq : q = mr + ns : s.

Solution 16

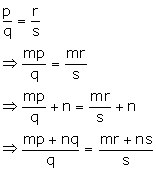
Hence, mp + nq : q = mr + ns : s.

Question 17

If p + r = mq and ; then prove that p : q = r : s.

Solution 17

Hence, proved.