Find the sum of G.P.:
1 + 3 + 9 + 27 + ………. to 12 terms
Find the sum of G.P.:
0.3 + 0.03 + 0.003 + 0.0003 +….. to 8 items.
Find the sum of G.P.:
Find the sum of G.P.:
Find the sum of G.P.:
Find the sum of G.P.:
How many terms of the geometric progression 1 + 4 + 16 + 64 + …….. must be added to get sum equal to 5461?
A boy spends Rs.10 on first day, Rs.20 on second day, Rs.40 on third day and so on. Find how much, in all, will he spend in 12 days?
A geometric progression has common ratio = 3 and last term = 486. If the sum of its terms is 728; find its first term.
Find the sum of G.P.: 3, 6, 12, …… 1536.
How many terms of the series 2 + 6 + 18 + …………… must be taken to make the sum equal to 728?
In a G.P., the ratio between the sum of first three terms and that of the first six terms is 125 : 152. Find its common ratio.
If the sum of 1+ 2 + 22 + ….. + 2n-1 is 255,find the value of n.
Find the geometric mean between:
Find the geometric mean between:
Find the geometric mean between:
2a and 8a3
The first term of a G.P. is -3 and the square of the second term is equal to its 4th term. Find its 7th term.
Find the 5th term of the G.P. ![]()
First term (a) = ![]()
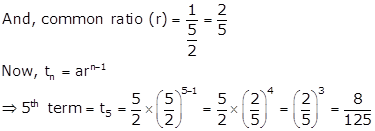
The first two terms of a G.P. are 125 and 25 respectively. Find the 5th and the 6th terms of the G.P.
First term (a) = 125
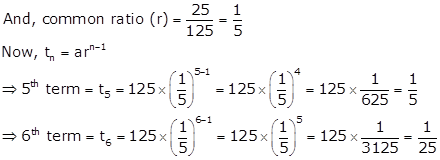
![]()
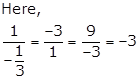
Thus, the given sequence is a G.P. with ![]()
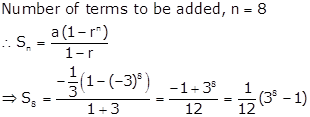
The first term of a G.P. is 27. If the 8th term be ![]() , what will be the sum of 10 terms?
, what will be the sum of 10 terms?
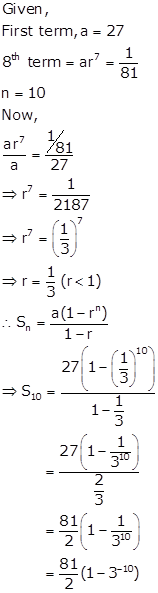
Find a G.P. for which the sum of first two terms is -4 and the fifth term is 4 times the third term.
Let the five terms of the given G.P. be
![]()
Given, sum of first two terms = -4
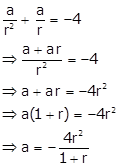
And, 5th term = 4(3rd term)
⇒ ar2 = 4(a)
⇒ r2 = 4
⇒ r = ±2
When r = +2,
![]()
When r = -2,
![]()
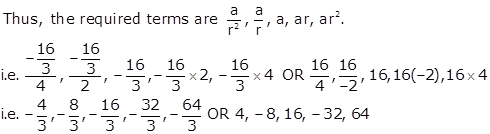
No comments:
Post a Comment