Chapter 6 - Solving (simple) Problems (Based on Quadratic Equations) Exercise Ex. 6(A)

Question 1

The product of two consecutive integers is 56. Find the integers.

Solution 1

Let the two consecutive integers be x and x + 1.

From the given information,

x(x + 1) = 56

x² + x - 56 = 0

(x + 8) (x - 7) = 0

x = -8 or 7

Thus, the required integers are - 8 and -7; 7 and 8.

Question 2

The sum of the squares of two consecutive natural numbers is 41. Find the numbers.

Solution 2

Let the numbers be x and x + 1.

From the given information,

x² + (x + 1)² = 41

2x² + 2x + 1 - 41 = 0

x² + x - 20 = 0

(x + 5) (x - 4) = 0

x = -5, 4

But, -5 is not a natural number. So, x = 4.

Thus, the numbers are 4 and 5.

Question 3

Find the two natural numbers which differ by 5 and the sum of whose squares is 97.

Solution 3

Let the two numbers be x and x + 5.

From the given information,

x² + (x + 5)² = 97

2x² + 10x + 25 - 97 = 0

2x² + 10x - 72 = 0

x² + 5x - 36 = 0

(x + 9) (x - 4) = 0

x = -9 or 4

Since, -9 is not a natural number. So, x = 4.

Thus, the numbers are 4 and 9.

Question 4

The sum of a number and its reciprocal is 4.25. Find the number.

Solution 4

Let the numbers be x and 

From the given information,

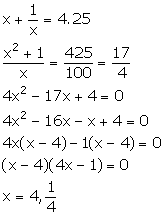
x = 4 

x =   x = 4

Thus, the numbers are 4 and 

Question 5

Two natural numbers differ by 3. Find the numbers, if the sum of their reciprocals is 

Solution 5

Let the numbers be x and x + 3.

From the given information,

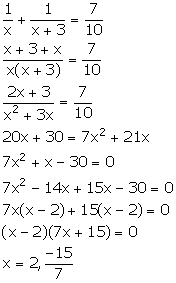
Since, x is a natural number, so x = 2.

Thus, the numbers are 2 and 5.

Question 6

Divide 15 into two parts such that the sum of their reciprocals is 

Solution 6

Let the two parts be x and x - 15.

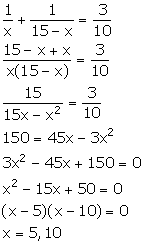
x = 5  One part = 5 and other part = 10

x = 10  One part = 10 and other part = 5

Thus, the required two parts are 5 and 10.

Question 7

The sum of the square of two positive integers is 208. If the square of larger number is 18 times the smaller number, find the numbers.

Solution 7

Let the two numbers be x and y, y being the bigger number. From the given information,

x² + y² = 208 ..... (i)

y² = 18x ..... (ii)

From (i), we get y²=208 - x². Putting this in (ii), we get,

208 - x² = 18x

 x² + 18x - 208 = 0

 x² + 26X - 8X - 208 = 0

 x(x + 26) - 8(x + 26) = 0

 (x - 8)(x + 26) = 0

 x can't be a negative number , hence x = 8

Putting x = 8 in (ii), we get y² = 18 x 8=144

 y = 12, since y is a positive integer

Hence, the two numbers are 8 and 12.

Question 8

The sum of the squares of two consecutive positive even numbers is 52. Find the numbers.

Solution 8

Let the consecutive positive even numbers be x and x + 2.

From the given information,

x² + (x + 2)² = 52

2x² + 4x + 4 = 52

2x² + 4x - 48 = 0

x² + 2x - 24 = 0

(x + 6) (x - 4) = 0

x = -6, 4

Since, the numbers are positive, so x = 4.

Thus, the numbers are 4 and 6.

Question 9

Find two consecutive positive odd numbers, the sum of whose squares is 74.

Solution 9

Let the consecutive positive odd numbers be x and x + 2.

From the given information,

x² + (x + 2)² = 74

2x² + 4x + 4 = 74

2x² + 4x - 70 = 0

x² + 2x - 35 = 0

(x + 7)(x - 5) = 0

x = -7, 5

Since, the numbers are positive, so, x = 5.

Thus, the numbers are 5 and 7.

Question 10

The denominator of a positive fraction is one more than twice the numerator. If the sum of the fraction and its reciprocal is 2.9; find the fraction.

Solution 10

Let the required fraction be.

From the given information,

 

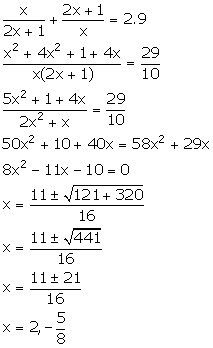
Thus, the required fraction is .

Question 11

Three positive numbers are in the ratio. Find the numbers if the sum of their squares is 244.

Solution 11

Given, three positive numbers are in the ratio

Let the numbers be 6x, 4x and 3x.

From the given information,

(6x)² + (4x)² + (3x)² = 244

36x² + 16x² + 9x² = 244

61x² = 244

x² = 4

x = 

Since, the numbers are positive, so x = 2.

Thus, the numbers are 12, 8 and 6.

Question 12

Divide 20 into two parts such that three times the square of one part exceeds the other part by 10.

Solution 12

Let the two parts be x and y.

From the given information,

x + y = 20 

3x² = (20 - x) + 10

3x² = 30 - x

3x² + x - 30 = 0

3x² - 9x + 10x - 30 = 0

3x(x - 3) + 10(x - 3) = 0

(x - 3) (3x + 10) = 0

x = 3, 

Since, x cannot be equal to, so, x = 3.

Thus, one part is 3 and other part is 20 - 3 = 17.

Question 13

Three consecutive natural numbers are such that the square of the middle number exceeds the difference of the squares of the other two by 60.

Assume the middle number to be x and form a quadratic equation satisfying the above statement. Hence; find the three numbers.

Solution 13

Let the numbers be x - 1, x and x + 1.

From the given information,

x² = (x + 1)² - (x - 1)² + 60

x² = x² + 1 + 2x - x² - 1 + 2x + 60

x² = 4x + 60

x² - 4x - 60 = 0

(x - 10) (x + 6) = 0

x = 10, -6

Since, x is a natural number, so x = 10.

Thus, the three numbers are 9, 10 and 11.

Question 14

Out of three consecutive positive integers, the middle number is p. If three times the square of the largest is greater than the sum of the squares of the other two numbers by 67; calculate the value of p.

Solution 14

Let the numbers be p - 1, p and p + 1.

From the given information,

3(p + 1)² = (p - 1)² + p² + 67

3p² + 6p + 3 = p² + 1 - 2p + p² + 67

p² + 8p - 65 = 0

(p + 13)(p - 5) = 0

p = -13, 5

Since, the numbers are positive so p cannot be equal to -13.

Thus, p = 5.

Question 15

A can do a piece of work in 'x' days and B can do the same work in (x + 16) days. If both working together can do it in 15 days; calculate 'x'.

Solution 15

Work done by A in one day = 

Work done by B in one day = 

Together A and B can do the work in 15 days. Therefore, we have:

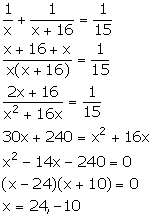
Since, x cannot be negative.

Thus, x = 24.

Question 16

One pipe can fill a cistern in 3 hours less than the other. The two pipes together can fill the cistern in 6 hours 40 minutes. Find the time that each pipe will take to fill the cistern.

Solution 16

Let one pipe fill the cistern in x hours and the other fills it in (x - 3) hours.

Given that the two pipes together can fill the cistern in 6 hours 40 minutes, i.e., 

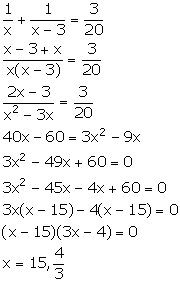
If x =, then x - 3 =, which is not possible.

So, x = 15.

Thus, one pipe fill the cistern in 15 hours and the other fills in (x - 3) = 15 - 3 = 12 hours.

Question 17

A positive number is divided into two parts such that the sum of the squares of the two parts is 20. The square of the larger part is 8 times the smaller part. Taking x as the smaller part of the two parts, find the number.

Solution 17

Let the smaller part be x.

Then, (larger part)² = 8x

\ larger part = 

Now, the sum of the squares of both the terms is given to be 208

Thus, the required number is 2 + 4 = 6.