Chapter 6 - Solving (simple) Problems (Based on Quadratic Equations) Exercise Ex. 6(D)

Question 1

The sum S of n successive odd numbers starting from 3 is given by the relation: S = n(n + 2). Determine n, if the sum is 168

Solution 1

From the given information, we have:

n(n + 2) = 168

n² + 2n - 168 = 0

n² + 14n - 12n - 168 = 0

n(n + 14) - 12(n + 14) = 0

(n + 14) (n - 12) = 0

n = -14, 12

But, n cannot be negative.

Therefore, n = 12.

Question 2

A stone is thrown vertically downwards and the formula d = 16t² + 4t gives the distance, d metres, that it falls in t seconds. How long does it take to fall 420 metres?

Solution 2

From the given information,

16t² + 4t = 420

4t² + t - 105 = 0

4t² - 20t + 21t - 105 = 0

4t(t - 5) + 21(t - 5) = 0

(4t + 21)(t - 5) = 0

t = , 5

But, time cannot be negative.

Thus, the required time taken is 5 seconds.

Question 3

The product of the digits of a two digit number is 24. If its unit's digit exceeds twice its ten's digit by 2; find the number.

Solution 3

Let the ten's and unit's digit of the required number be x and y respectively.

From the given information,

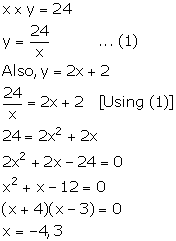
The digit of a number cannot be negative, so, x = 3.

Thus, the required number is 38.

Question 4

The ages of two sisters are 11 years and 14 years. In how many years time will the product of their ages be 304?

Solution 4

The ages of two sisters are 11 years and 14 years.

Let in x number of years the product of their ages be 304.

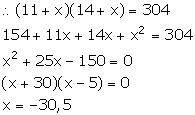
But, the number of years cannot be negative. So, x = 5.

Hence, the required number of years is 5 years.

Question 5

One year ago, a man was 8 times as old as his son. Now his age is equal to the square of his son's age. Find their present ages.

Solution 5

Let the present age of the son be x years.

Present age of man = x² years

One year ago,

Son's age = (x - 1) years

Man's age = (x² - 1) years

It is given that one year ago; a man was 8 times as old as his son.

 (x² - 1) = 8(x - 1)

x² - 8x - 1 + 8 = 0

x² - 8x + 7 = 0

(x - 7) (x - 1) = 0

x = 7, 1

If x = 1, then x² = 1, which is not possible as father's age cannot be equal to son's age.

So, x = 7.

Present age of son = x years = 7 years

Present age of man = x² years = 49 years.

Question 6

The age of the father is twice the square of the age of his son. Eight years hence, the age of the father will be 4 years more than three times the age of the son. Find their present ages.

Solution 6

Let the present age of the son be x years.

 Present age of father = 2x² years

Eight years hence,

Son's age = (x + 8) years

Father's age = (2x² + 8) years

It is given that eight years hence, the age of the father will be 4 years more than three times the age of the son.

 2x² + 8 = 3(x + 8) +4

2x² + 8 = 3x + 24 +4

2x² - 3x - 20 = 0

2x² - 8x + 5x - 20 = 0

2x(x - 4) + 5(x - 4) = 0

(x - 4) (2x + 5) = 0

x = 4, 

But, the age cannot be negative, so, x = 4.

 Present age of son = 4 years

Present age of father = 2(4)² years = 32 years

Question 7

The speed of a boat in still water is 15 km/hr. It can go 30 km upstream and return downstream to the original point in 4 hours 30 minutes. Find the speed of the stream.

Solution 7

Let the speed of the stream be x km/hr.

 Speed of the boat downstream = (15 + x) km/hr

Speed of the boat upstream = (15 - x) km/hr

Time taken to go 30 km downstream = 

Time taken to come back = 

From the given information,

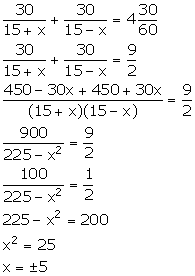
But, x cannot be negative, so, x = 5.

Thus, the speed of the stream is 5 km/hr.

Question 8

Mr. Mehra sends his servant to the market to buy oranges worth Rs 15. The servant having eaten three oranges on the way. Mr. Mehra pays Rs 25 paise per orange more than the market price.

Taking x to be the number of oranges which Mr. Mehra receives, form a quadratic equation in x. Hence, find the value of x.

Solution 8

Number of oranges = y

Cost of one orange = 

The servant ate 3 oranges, so Mr. Mehra received (y - 3) oranges.

So, x = y - 3  y = x + 3 ...(1)

Cost of one orange paid by Mr. Mehra = 

                                                         =

Now, Mr. Mehra pays a total of Rs 15.

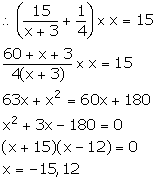
But, the number of oranges cannot be negative. So, x = 12.

Question 9

Rs 250 is divided equally among a certain number of children. If there were 25 children more, each would have received 50 paise less. Find the number of children.

Solution 9

Let the number of children be x.

It is given that Rs 250 is divided amongst x students.

So, money received by each child = Rs

If there were 25 children more, then

Money received by each child = Rs

From the given information,

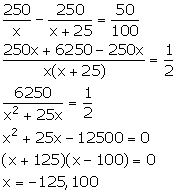
Since, the number of students cannot be negative, so, x = 100.

Hence, the number of students is 100.

Question 10

An employer finds that if he increased the weekly wages of each worker by Rs 5 and employs five workers less, he increases his weekly wage bill from Rs 3,150 to Rs 3,250. Taking the original weekly wage of each worker as Rs x; obtain an equation in x and then solve it to find the weekly wages of each worker.

Solution 10

Original weekly wage of each worker = Rs x

Original weekly wage bill of employer = Rs 3150

Number of workers = 

New weekly wage of each worker = Rs (x + 5)

New weekly wage bill of employer = Rs 3250

Number of workers = 

From the given condition,

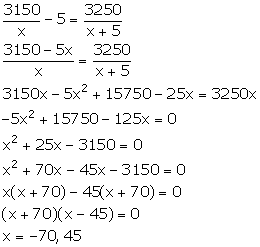
Since, wage cannot be negative, x = 45.

Thus, the original weekly wage of each worker is Rs 45.

Question 11

A trader bought a number of articles for Rs 1,200. Ten were damaged and he sold each of the remaining articles at Rs 2 more than what he paid for it, thus getting a profit of Rs 60 on whole transaction.

Taking the number of articles he bought as x, form an equation in x and solve it.

Solution 11

Number of articles bought by the trader = x

It is given that the trader bought the articles for Rs 1200.

So, cost of one article = Rs

Ten articles were damaged. So, number of articles left = x - 10

Selling price of each of (x - 10) articles = Rs

Selling price of (x - 10) articles = Rs (x - 10) 

Profit = Rs 60

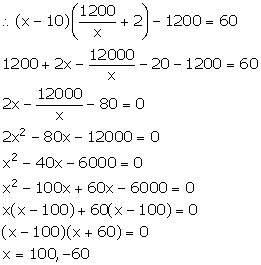
Number of articles cannot be negative. So, x = 100.

Question 12

The total cost price of a certain number of identical articles is Rs 4800. By selling the articles at Rs 100 each, a profit equal to the cost price of 15 articles is made. Find the number of articles bought.

Solution 12

Let the number of articles bought be x.

Total cost price of x articles = Rs 4800

Cost price of one article = Rs

Selling price of each article = Rs 100

Selling price of x articles = Rs 100x

Given, Profit = C.P. of 15 articles

 100x - 4800 = 15 

100x² - 4800x = 15  4800

x² - 48x - 720 = 0

x² - 60x + 12x - 720 = 0

x(x - 60) + 12(x - 60) = 0

(x - 60) (x + 12) = 0

x = 60, -12

Since, number of articles cannot be negative. So, x = 60.

Thus, the number of articles bought is 60.