Chapter 6 - Solving (simple) Problems (Based on Quadratic Equations) Exercise Ex. 6(C)

Question 1

The speed of an ordinary train is x km per hr and that of an express train is (x + 25) km per hr.

(i) Find the time taken by each train to cover 300 km.

(ii) If the ordinary train takes 2 hrs more than the express train; calculate speed of the express train.

Solution 1

(i) Speed of ordinary train = x km/hr

Speed of express train = (x + 25) km/hr

Distance = 300 km

We know:

 Time taken by ordinary train to cover 300 km = 

Time taken by express train to cover 300 km = 

(ii) Given that the ordinary train takes 2 hours more than the express train to cover the distance.

Therefore,

But, speed cannot be negative. So, x = 50.

 Speed of the express train = (x + 25) km/hr = 75 km/hr

Question 2

If the speed of a car is increased by 10 km per hr, it takes 18 minutes less to cover a distance of 36 km. Find the speed of the car.

Solution 2

Let the speed of the car be x km/hr.

Distance = 36 km

Time taken to cover a distance of 36 km = 

New speed of the car = (x + 10) km/hr

New time taken by the car to cover a distance of 36 km = 

From the given information, we have:

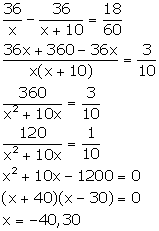
But, speed cannot be negative. So, x = 30.

Hence, the original speed of the car is 30 km/hr.

Question 3

If the speed of an aeroplane is reduced by 40 km/hr, it takes 20 minutes more to cover 1200 km. Find the speed of the aeroplane.

Solution 3

Let the original speed of the aeroplane be x km/hr.

Time taken to cover a distance of 1200 km = 

Let the new speed of the aeroplane be (x - 40) km/hr.

Time taken to cover a distance of 1200 km = 

From the given information, we have:

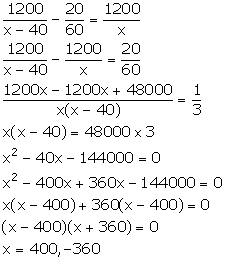
But, speed cannot be negative. So, x = 400.

Thus, the original speed of the aeroplane is 400 km/hr.

Question 4

A car covers a distance of 400 km at a certain speed. Had the speed been 12 km/h more, the time taken for the journey would have been 1 hour 40 minutes less. Find the original speed of the car.

Solution 4

 

Let x km/h be the original speed of the car.

We know that,

It is given that the car covers a distance of 400 km with the speed of x km/h.

Thus, the time taken by the car to complete 400 km is

Now, the speed is increased by 12 km.

Also given that, increasing the speed of the car will decrease the time taken by 1 hour 40 minutes.

 

Hence,

Question 5

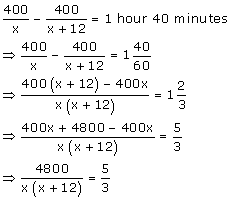
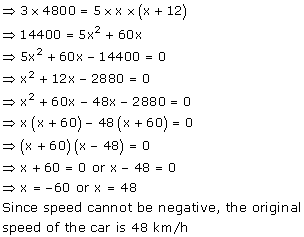
A girl goes to her friend's house, which is at a distance of 12 km. She covers half of the distance at a speed of x km/hr and the remaining distance at a speed of (x + 2) km/hr. If she takes 2 hrs 30 minutes to cover the whole distance, find 'x'.

Solution 5

We know:

Given, the girl covers a distance of 6 km at a speed x km/ hr.

Time taken to cover first 6 km = 

Also, the girl covers the remaining 6 km distance at a speed (x + 2) km/ hr.

Time taken to cover next 6 km = 

Total time taken to cover the whole distance = 2 hrs 30 mins = 

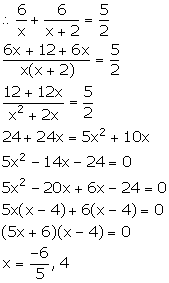
Since, speed cannot be negative. Therefore, x = 4.

Question 6

A car made a run of 390 km in 'x' hours. If the speed had been 4 km/hour more, it would have taken 2 hours less for the journey. Find 'x'.

Solution 6

Let the original speed of the car be y km/hr.

We know:

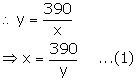
New speed of the car = (y + 4) km/hr

New time taken by the car to cover 390 km = 

From the given information,

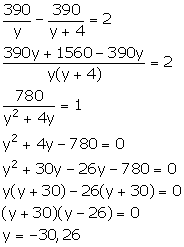
Since, time cannot be negative, so y = 26.

From (1), we have:

Question 7

A goods train leaves a station at 6 p.m., followed by an express train which leaved at 8 p.m. and travels 20 km/hour faster than the goods train. The express train arrives at a station, 1040 km away, 36 minutes before the goods train. Assuming that the speeds of both the train remain constant between the two stations; calculate their speeds.

Solution 7

Let the speed of goods train be x km/hr. So, the speed of express train will be (x + 20) km/hr.

Distance = 1040 km

We know:

Time taken by goods train to cover a distance of 1040 km = 

Time taken by express train to cover a distance of 1040 km = 

It is given that the express train arrives at a station 36 minutes before the goods train. Also, the express train leaves the station 2 hours after the goods train. This means that the express train arrives at the station  before the goods train.

Therefore, we have:

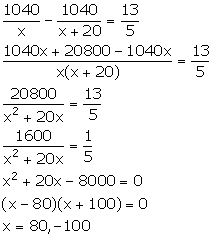
Since, the speed cannot be negative. So, x = 80.

Thus, the speed of goods train is 80 km/hr and the speed of express train is 100 km/hr.

Question 8

A man bought an article for Rs x and sold it for Rs 16. If his loss was x per cent, find the cost price of the article.

Solution 8

C.P. of the article = Rs x

S.P. of the article = Rs 16

Loss = Rs (x - 16)

We know:

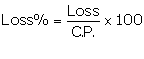
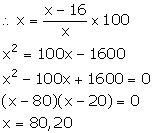
Thus, the cost price of the article is Rs 20 or Rs 80.

Question 9

A trader bought an article for Rs x and sold it for Rs 52, thereby making a profit of (x - 10) per cent on his outlay. Calculate the cost price.

Solution 9

C.P. of the article = Rs x

S.P. of the article = Rs 52

Profit = Rs (52 - x)

We know:

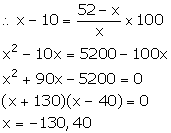
Since, C.P. cannot be negative. So, x = 40.

Thus, the cost price of the article is Rs 40.

Question 10

By selling a chair for Rs 75, Mohan gained as much per cent as its cost. Calculate the cost of the chair.

Solution 10

Let the C.P. of the chair be Rs x

S.P. of chair = Rs 75

Profit = Rs (75 - x)

We know:

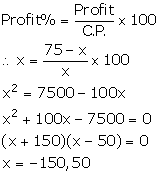
But, C.P. cannot be negative. So, x = 50.

Hence, the cost of the chair is Rs 50.