Chapter 6 - Solving (simple) Problems (Based on Quadratic Equations) Exercise Ex. 6(B)

Question 1

The sides of a right-angled triangle containing the right angle are 4x cm and (2x - 1) cm. If the area of the triangle is 30 cm²; calculate the lengths of its sides.

Solution 1

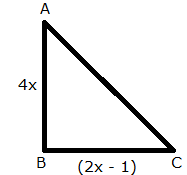
Area of triangle = 30 cm²

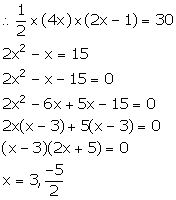
But, x cannot be negative, so x = 3.

Thus, we have:

AB = 4  3 cm = 12 cm

BC = (2  3 - 1) cm = 5 cm

CA =  (Using Pythagoras theorem)

Question 2

The hypotenuse of a right-angled triangle is 26 cm and the sum of other two sides is 34 cm. Find the lengths of its sides.

Solution 2

Hypotenuse = 26 cm

The sum of other two sides is 34 cm.

So, let the other two sides be x cm and (34 - x) cm.

Using Pythagoras theorem,

(26)² = x² + (34 - x)²

676 = x² + x² + 1156 - 68x

2x² - 68x + 480 = 0

x² - 34x + 240 = 0

x² - 10x - 24x + 240 = 0

x(x - 10) - 24(x - 10) = 0

(x - 10) (x - 24) = 0

x = 10, 24

When x = 10, (34 - x) = 24

When x = 24, (34 - x) = 10

Thus, the lengths the three sides of the right-angled triangle are 10 cm, 24 cm and 26 cm.

Question 3

The sides of a right-angled triangle are (x - 1) cm, 3x cm and (3x + 1) cm. Find:

(i) the value of x,

(ii) the lengths of its sides,

(iii) its area.

Solution 3

Longer side = Hypotenuse = (3x + 1) cm

Lengths of other two sides are (x - 1) cm and 3x cm.

Using Pythagoras theorem,

(3x + 1)² = (x - 1)² + (3x)²

9x² + 1 + 6x = x² + 1 - 2x + 9x²

x² - 8x = 0

x(x - 8) = 0

x = 0, 8

But, if x = 0, then one side = 3x = 0, which is not possible.

So, x = 8

Thus, the lengths of the sides of the triangle are (x - 1) cm = 7 cm, 3x cm = 24 cm and (3x + 1) cm = 25 cm.

Area of the triangle = 

Question 4

The hypotenuse of a right-angled triangle exceeds one side by 1 cm and the other side by 18 cm; find the lengths of the sides of the triangle.

Solution 4

Let the hypotenuse of a triangle be x cm.

From the given information,

Length of one side = (x - 1) cm

Length of other side = (x - 18) cm

 

Using Pythagoras theorem,

x² = (x - 1)² + (x - 18)²

x² = x² + 1 - 2x + x² + 324 - 36x

x² - 38x + 325 = 0

x² - 13x - 25x + 325 = 0

x(x - 13) - 25(x - 13) = 0

(x - 13) (x - 25) = 0

x = 13, 25

 

When x = 13, x - 18 = 13 - 18 = -5, which being negative, is not possible.

 

So, x = 25

 

Thus, the lengths of the sides of the triangle are x = 25 cm, (x - 1) = 24 cm and (x - 18) = 7 cm.

Question 5

The diagonal of a rectangle is 60 m more than its shorter side and the larger side is 30 m more than the shorter side. Find the sides of the rectangle.

Solution 5

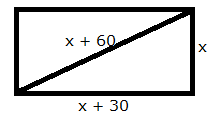
Let the shorter side be x m.

Length of the other side = (x + 30) m

Length of hypotenuse = (x + 60) m

Using Pythagoras theorem,

(x + 60)² = x² + (x + 30)²

x² + 3600 + 120x = x² + x² + 900 + 60x

x² - 60x - 2700 = 0

x² - 90x + 30x - 2700 = 0

x(x - 90) + 30(x - 90) = 0

(x - 90) (x + 30) = 0

x = 90, -30

But, x cannot be negative. So, x = 90.

Thus, the sides of the rectangle are 90 m and (90 + 30) m = 120 m.

Question 6

The perimeter of a rectangle is 104 m and its area is 640 m². Find its length and breadth.

Solution 6

Let the length and the breadth of the rectangle be x m and y m.

Perimeter = 2(x + y) m

104 = 2(x + y)

x + y = 52

y = 52 - x

 

Area = 640 m²

 xy = 640

x(52 - x) = 640

x² - 52x + 640 = 0

x² - 32x - 20x + 640 = 0

x(x - 32) - 20 (x - 32) = 0

(x - 32) (x - 20) = 0

x = 32, 20

 

When x = 32, y = 52 - 32 = 20

When x = 20, y = 52 - 20 = 32

 

Thus, the length and breadth of the rectangle are 32 m and 20 m.

Question 7

A footpath of uniform width runs round the inside of a rectangular field 32 m long and 24 m wide. If the path occupies 208 m², find the width of the footpath.

Solution 7

Let w be the width of the footpath.

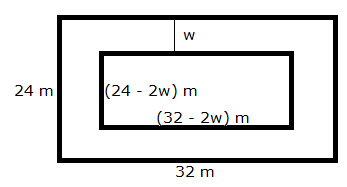
Area of the path = Area of outer rectangle - Area of inner rectangle

208 = (32)(24) - (32 - 2w)(24 - 2w)

208 = 768 - 768 + 64w + 48w - 4w²

4w² - 112w + 208 = 0

w² - 28w + 52 = 0

w² - 26w - 2w + 52 = 0

w(w - 26) - 2(w - 26) = 0

(w - 26) (w - 2) = 0

w = 26, 2

If w = 26, then breadth of inner rectangle = (24 - 52) m = -28 m, which is not possible.

Hence, the width of the footpath is 2 m.

Question 8

Two squares have sides x cm and (x + 4) cm. The sum of their area is 656 sq. cm. Express this as an algebraic equation in x and solve the equation to find the sides of the squares.

Solution 8

Given that, two squares have sides x cm and (x + 4) cm.

Sum of their area = 656 cm²

 x² + (x + 4)² = 656

x² + x² + 16 + 8x = 656

2x² + 8x - 640 = 0

x² + 4x - 320 = 0

x² + 20x - 16x - 320 = 0

x(x + 20) - 16(x + 20) = 0

(x + 20) (x - 16) = 0

x = -20, 16

But, x being side, cannot be negative.

So, x = 16

Thus, the sides of the two squares are 16 cm and 20 cm.

Question 9

The dimensions of a rectangular field are 50 m and 40 m. A flower bed is prepared inside this field leaving a gravel path of uniform width all around the flower bed. The total cost of laying the flower bed and gravelling the path at Rs 30 and Rs 20 per square metre, respectively, is Rs 52,000. Find the width of the gravel path.

Solution 9

Let the width of the gravel path be w m.

Length of the rectangular field = 50 m

Breadth of the rectangular field = 40 m

Let the length and breadth of the flower bed be x m and y m respectively.

 

Therefore, we have:

x + 2w = 50 ... (1)

y + 2w = 40 ... (2)

 

Also, area of rectangular field = 50 m  40 m = 2000 m²

 

Area of the flower bed = xy m²

Area of gravel path = Area of rectangular field - Area of flower bed = (2000 - xy) m²

 

Cost of laying flower bed + Gravel path = Area x cost of laying per sq. m

 52000 = 30  xy + 20  (2000 - xy)

52000 = 10xy + 40000

xy = 1200

Using (1) and (2), we have:

(50 - 2w) (40 - 2w) = 1200

2000 - 180w + 4w² = 1200

4w² - 180w + 800 = 0

w² - 45w + 200 = 0

w² - 5w - 40w + 200 = 0

w(w - 5) - 40(w - 5) = 0

(w - 5) (w - 40) = 0

w = 5, 40

 

If w = 40, then x = 50 - 2w = -30, which is not possible.

Thus, the width of the gravel path is 5 m.

Question 10

An area is paved with square tiles of a certain size and the number required is 128. If the tiles had been 2 cm smaller each way, 200 tiles would have been needed to pave the same area. Find the size of the larger tiles.

Solution 10

Let the size of the larger tiles be x cm.

Area of larger tiles = x² cm²

Number of larger tiles required to pave an area is 128.

So, the area needed to be paved = 128 x² cm² .... (1)

 

Size of smaller tiles = (x - 2)cm

Area of smaller tiles = (x - 2)² cm²

Number of larger tiles required to pave an area is 200.

So, the area needed to be paved = 200 (x - 2)² cm² .... (2)

 

Therefore, from (1) and (2), we have:

128 x² = 200 (x - 2)²

128 x² = 200x² + 800 - 800x

72x² - 800x + 800 = 0

9x² - 100x + 100 = 0

9x² - 90x - 10x + 100 = 0

9x(x - 10) - 10(x - 10) = 0

(x - 10)(9x - 10) = 0

x = 10, 

If , then , which is not possible.

Hence, the size of the larger tiles is 10 cm.

Question 11

A farmer has 70 m of fencing, with which he encloses three sides of a rectangular sheep pen; the fourth side being a wall. If the area of the pen is 600 sq. m, find the length of its shorter side.

Solution 11

Let the length and breadth of the rectangular sheep pen be x and y respectively.

From the given information,

x + y + x = 70

2x + y = 70 ... (1)

 

Also, area = xy = 600

Using (1), we have:

x (70 - 2x) = 600

70x - 2x² = 600

2x² - 70x + 600 = 0

x² - 35x + 300 = 0

x² - 15x - 20x + 300 = 0

x(x - 15) - 20(x - 15) = 0

(x - 15)(x - 20) = 0

x = 15, 20

If x = 15, then y = 70 - 2x = 70 - 30 = 40

If x = 20, then y = 70 - 2x = 70 - 40 = 30

 

Thus, the length of the shorter side is 15 m when the longer side is 40 m. The length of the shorter side is 20 m when the longer side is 30 m.

Question 12

A square lawn is bounded on three sides by a path 4 m wide. If the area of the path is that of the lawn, find the dimensions of the lawn.

Solution 12

Let the side of the square lawn be x m.

Area of the square lawn = x² m²

The square lawn is bounded on three sides by a path which is 4 m wide.

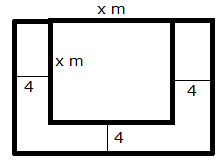
Area of outer rectangle = (x + 4) (x + 8) = x² + 12x + 32

Area of path = x² + 12x + 32 - x² = 12x + 32

From the given information, we have:

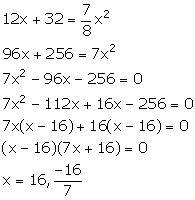
Since, x cannot be negative. So, x = 16 m.

Thus, each side of the square lawn is 16 m.

Question 13

The area of a big rectangular room is 300 m². If the length were decreased by 5 m and the breadth increased by 5 m; the area would be unaltered. Find the length of the room.

Solution 13

Let the original length and breadth of the rectangular room be x m and y m respectively.

Area of the rectangular room = xy = 300

 

New length = (x - 5) m

New breadth = (y + 5) m

New area = (x - 5) (y + 5) = 300 (given)

Using (1), we have:

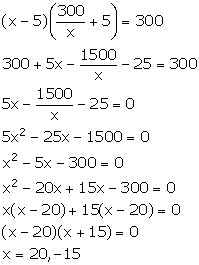
But, x cannot be negative. So, x = 20.

Thus, the length of the room is 20 m.