Chapter 2 - Banking (Recurring Deposit Accounts) Exercise Ex. 2(A)

Question 1

Manish opens a Recurring Deposit Account with the Bank of Rajasthan and deposits  600 per month for 20 months. Calculate the maturity value of this account, if the bank pays interest at the rate of 10% per annum.

Solution 1

Installment per month(P) = Rs. 600

Number of months(n) = 20

Rate of interest (r) = 10% p.a.

The amount that Manish will get at the time of maturity

=Rs (600 x 20)+ Rs 1,050

=Rs 12,000+ Rs 1,050

= Rs 13,050 

Question 2

Mrs. Mathew opened a Recurring Deposit Account in a certain bank and deposited  640 per month for 4¹/₂ years. Find the maturity value of this account, if the bank pays interest at the rate of 12% per year.

Solution 2

Installment per month(P) = Rs 640

Number of months(n) = 4.5 × 12 = 54

Rate of interest(r)= 12% p.a.

The amount that Manish will get at the time of maturity

=Rs (640 x 54)+ Rs 9,504

=Rs 34,560+ Rs 9,504

= Rs 44,064 

Question 3

 Each of A and B both opened recurring deposit accounts in a bank. If A deposited  1,200 per month for 3 years and B deposited  1,500 per month for  years; find, on maturity, who will get more amount and by how much? The rate of interest paid by the bank is 10% per annum.

Solution 3

For A

Installment per month(P) = Rs 1,200

Number of months(n) = 3 × 12 = 36

Rate of interest(r)= 10% p.a.

The amount that A will get at the time of maturity

=Rs (1,200 x 36)+ Rs 6,660

=Rs 43,200+ Rs 6,660

= Rs 49,860

For B

Installment per month(P) = Rs 1,500

Number of months(n) = 2.5 × 12 = 30

Rate of interest(r)= 10% p.a.

The amount that B will get at the time of maturity

=Rs(1,500 x 30)+ Rs 5,812.50

=Rs 45,000+ Rs 5,812.50

= Rs 50,812.50

Difference between both amounts= Rs 50,812.50 - Rs 49,860

= Rs 952.50

 

Then B will get more money than A by Rs 952.50 

Question 4

Ashish deposits a certain sum of money every month is a Recurring Deposit Account for a period of 12 months. If the bank pays interest at the rate of 11% p.a. and Ashish gets  12,715 as the maturity value of this account, what sum of money did money did he pay every month?

Solution 4

Let Installment per month(P) = Rs y

Number of months(n) = 12

Rate of interest(r)= 11%p.a.

Maturity value= Rs (y x 12) + Rs 0.715 y = Rs 12.715 y

Given maturity value= Rs 12,715

Then Rs 12.715 y = Rs 12,715

Question 5

A man has a Recurring Deposit Account in a bank for 3½ years. If the rate of interest is 12% per annum and the man gets 10,206 on maturity, find the value of monthly installments.

Solution 5

Let Installment per month(P) = Rs y

Number of months(n) = 3.5 × 12 = 42

Rate of interest(r) = 12% p.a.

Maturity value= Rs(y x 42) + Rs 9.03y = Rs 51.03y

Given maturity value = Rs 10,206

 

Then Rs 51.03y = Rs 10206

 

Question 6

(i) Puneet has a Recurring Deposit Account in the Bank of Baroda and deposits 140 per month for 4 years. If he gets 8,092 on maturity, find the rate of interest given by the bank.

(ii) David opened a Recurring Deposit Account in a bank and deposited 300 per month for two years. If he received 7,725 at the time of maturity, find the rate of interest per annum.

Solution 6

(a) Installment per month(P) = Rs 140

Number of months(n) = 4 × 12 = 48

Let rate of interest(r)= r %p.a.

Maturity value= Rs (140 x 48) + Rs (137.20)r

Given maturity value= Rs 8,092

Then Rs(140 x 48)+Rs (137.20)r = Rs 8,092

137.20r = Rs 8,092 - Rs 6,720

 r = 

(b)

Installment per month(P) = Rs 300

Number of months(n) = 4 × 12 = 24

Let rate of interest(r)= r %p.a.

Maturity value= Rs (300 x 24)+Rs(75)r

Given maturity value = Rs 7,725

 

Then Rs(300 x 24) + Rs(75)r = Rs 7,725

 75 r = Rs 7,725 - Rs 7,200

 r = 

Question 7

Amit deposited 150 per month in a bank for 8 months under the Recurring Deposit Scheme. What will be the maturity value of his deposits, if the rate of interest is 8% per annum and interest is calculated at the end of every month?

Solution 7

Installment per month(P) = Rs 150

Number of months(n) = 8

Rate of interest(r)= 8% p.a.

The amount that Manish will get at the time of maturity

=Rs (150 x 8)+ Rs 36

=Rs 1,200+ Rs 36

= Rs 1,236

Question 8

Mrs. Geeta deposited 350 per month in a bank for 1 year and 3 months under the Recurring Deposit Scheme. If the maturity value of her deposits is 5,565; find the rate of interest per annum.

Solution 8

Installment per month(P) = Rs 350

Number of months(n) = 12 + 3 = 15

Let rate of interest(r)= r %p.a.

Maturity value= Rs (350 x 15) + Rs (35)r

Given maturity value= Rs 5,565

Then Rs (350 x 15) + Rs (35)r = Rs 5,565

35r = Rs 5,565 - Rs 5,250

 r = 

Question 9

A recurring deposit account of 1,200 per month has a maturity value of 12,440. If the rate of interest is 8% and the interest is calculated at the end of every month; find the time (in months) of this Recurring Deposit Account.

Solution 9

Installment per month(P) = Rs 1,200

Number of months(n) = n

Let rate of interest(r)= 8 %p.a.

Maturity value= Rs (1,200 x n) + Rs 4n (n + 1)= Rs (1200n + 4n² + 4n)

Given maturity value= Rs 12,440

Then 1200n + 4n² + 4n = 12,440

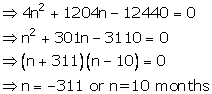
Then number of months = 10

Question 10

Mr. Gulati has a Recurring Deposit Account of 300 per month. If the rate of interest is 12% and the maturity value of this account is 8,100; find the time (in years) of this Recurring Deposit Account.

Solution 10

Installment per month(P) = Rs 300

Number of months(n) = n

Let rate of interest(r)= 12 %p.a.

Maturity value= Rs (300 x n) + Rs 1.5n(n + 1)

= Rs (300n + 1.5n² + 1.5n)

Given maturity value = Rs 8,100

Then 300n + 1.5n² + 1.5n = 8,100

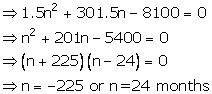
Then time = 2 years

Question 11

Mr. Gupta opened a recurring deposit account in a bank. He deposited 2,500 per month for two years. At the time of maturity he got 67,500. Find:

(i) the total interest earned by Mr. Gupta

(ii) the rate of interest per annum.

Solution 11

(i) Maturity value = Rs 67,500

Money deposited = Rs 2,500 x 24 = Rs 60,000

Then total interest earned = Rs 67,500 - Rs 60,000 = Rs 7,500 Ans.

(ii)

Installment per month(P) = Rs 2,500

Number of months(n) = 24

Let rate of interest(r)= r %p.a.

Then 625 r = 7500