Chapter 5 - Quadratic Equations Exercise Ex. 5(F)

Question 1: Solve-

(i) (x+5)(x-5)=24 

(ii)  

(iii)  

(iv) 

Solution 1

(i) Given: (x+5)(x-5)=24

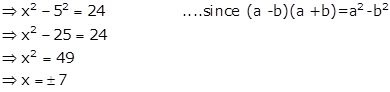
(ii)

Given: 

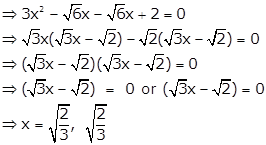
(iii)

Given: 

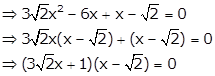
 or 

(iv) 

To find : x

Question 2

One root of the quadratic equation  is . Find the value of m. Also, find the other root of the equation. 

Solution 2

Given quadratic equation is  …. (i)

One of the roots of (i) is , so it satisfies (i)

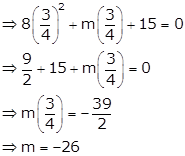
So, the equation (i) becomes 

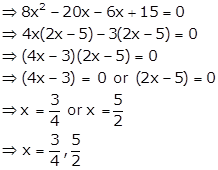
Hence, the other root is.

Question 3

One root of the quadratic equation  is -3, find its other root. 

Solution 3

Given quadratic equation is  …. (i)

One of the roots of (i) is -3, so it satisfies (i)

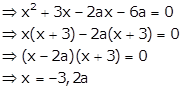
Hence, the other root is 2a.

Question 4

If and ;find the values of x. 

Solution 4

Given  i.e 

So, the given quadratic equation becomes

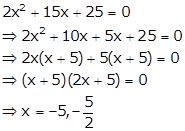
Hence, the values of x are  and.

Question 5

Find the solution of the equation; if and .

Solution 5

Given quadratic equation is ….. (i)

Also, given and 

 and 

So, the equation (i) becomes

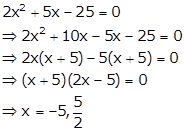
Hence, the solution of given quadratic equation are  and. 

Question 6

If m and n are roots of the equation where x ≠ 0 and x ≠ 2; find m × n. 

Solution 6

Given quadratic equation is 

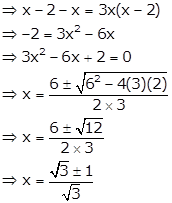
Since, m and n are roots of the equation, we have

 and 

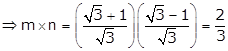
Hence, .

Question 7

Solve, using formula :

 

Solution 7

Given quadratic equation is 

Using quadratic formula,

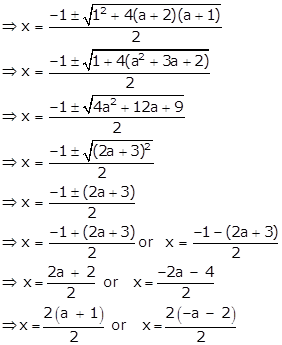
⇒ x = a + 1 or x = -a - 2 = -(a + 2)

Question 8

Solve the quadratic equation 

(i) When (integers)

(ii) When (rational numbers) 

Solution 8

Given quadratic equation is 

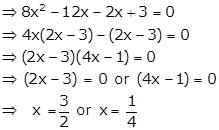
(i) When the equation  has no roots

(ii) When the roots of  are

or 

Question 9

Find the value of m for which the equation  has real and equal roots. 

Solution 9

Given quadratic equation is 

The quadratic equation has real and equal roots if its discriminant is zero.

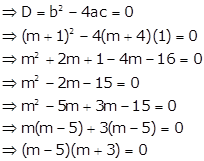
 or 

Question 10

Find the values of m for which equation  has equal roots. Also, find the roots of the given equation. 

Solution 10

Given quadratic equation is …. (i)

The quadratic equation has equal roots if its discriminant is zero

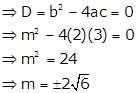
When , equation (i) becomes

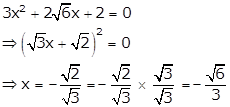
When , equation (i) becomes

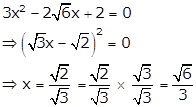
∴ x = 

Question 11

Find the value of k for which equation  has real roots. 

Solution 11

Given quadratic equation is …. (i)

The quadratic equation has real roots if its discriminant is greater than or equal to zero

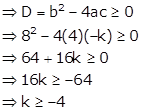
Hence, the given quadratic equation has real roots for.

Question 12

Find, using quadratic formula, the roots of the following quadratic equations, if they exist

(i) 

(ii)  

Solution 12

(i) Given quadratic equation is 

D = b² - 4ac = = 25 - 24 = 1

Since D > 0, the roots of the given quadratic equation are real and distinct.

Using quadratic formula, we have

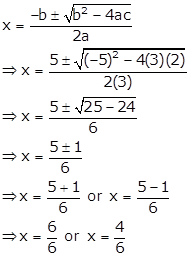
 or 

(ii) Given quadratic equation is 

D = b² - 4ac = = 16 - 20 = - 4

Since D < 0, the roots of the given quadratic equation does not exist.

Question 13

Solve :

(i)  and x > 0.

(ii)  and x < 0. 

Solution 13

(i) Given quadratic equation is 

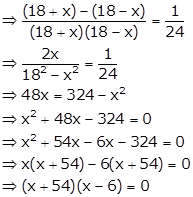
 or 

But as x > 0, so x can't be negative.

Hence, x = 6.

(ii) Given quadratic equation is 

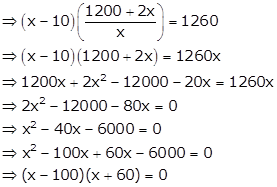
 or 

But as x < 0, so x can't be positive.

Hence,