⇒ (9x2 - 6x + 1) = 5x + 40
⇒ 9x2 - 11x - 39 =0; which is of the form ax2 + bx + c = 0.
∴ Given equation is a quadratic equation.
(ii) 5x2 - 8x = -3(7 - 2x)
⇒ 5x2 - 8x = 6x - 21
⇒ 5x2 - 14x + 21 =0; which is of the form ax2 + bx + c = 0.
∴ Given equation is a quadratic equation.
(iii) (x - 4)(3x + 1) = (3x - 1)(x +2)
⇒ 3x2 + x - 12x - 4 = 3x2 + 6x - x - 2
⇒ 16x + 2 =0; which is not of the form ax2 + bx + c = 0.
∴ Given equation is not a quadratic equation.
(iv) X2 + 5x – 5 = (x-3)2
![]() x2 + 5x – 5 =
x2 – 6x + 9
x2 + 5x – 5 =
x2 – 6x + 9
![]() 11x – 14 = 0; which is
not of the form ax2 + bx + c = 0
11x – 14 = 0; which is
not of the form ax2 + bx + c = 0
![]() Given equation is not a quadratic equation
Given equation is not a quadratic equation
(v) 7x3 - 2x2 + 10 = (2x - 5)2
⇒ 7x3 - 2x2 + 10 = 4x2 - 20x + 25
⇒ 7x3 - 6x2 + 20x - 15 = 0; which is not of the form ax2 + bx + c = 0.
∴ Given equation is not a quadratic equation.
(vi) (x - 1)2 + (x + 2)2 + 3(x +1) = 0
⇒ x2 - 2x + 1 + x2 + 4x + 4 + 3x + 3 = 0
⇒ 2x2 + 5x + 8 = 0; which is of the form ax2 + bx + c = 0.
∴ Given equation is a quadratic equation.
For x = 5 to be solution of the given quadratic equation it should satisfy the equation.
So, substituting x = 5 in the given equation, we get
L.H.S = (5)2 - 2(5) - 15
= 25 - 10 - 15
= 0
= R.H.S
Hence, x = 5 is a solution of the quadratic equation x2 - 2x - 15 = 0.
2x2 - 7x + 9 = 0
For x = -3 to be solution of the given quadratic equation it should satisfy the equation
So, substituting x = 5 in the given equation, we get
L.H.S=2(-3)2 - 7(-3) + 9
= 18 + 21 + 9
= 48
≠ R.H.S
Hence, x = -3 is not a solution of the quadratic equation 2x2 - 7x + 9 = 0.
If ![]() is a solution of equation 3x2 + mx + 2 = 0, find the value of m.
is a solution of equation 3x2 + mx + 2 = 0, find the value of m.
For x = ![]() to be solution of the given quadratic equation it should satisfy the equation
to be solution of the given quadratic equation it should satisfy the equation
So, substituting x = ![]() in the given equation, we get
in the given equation, we get
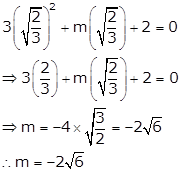
![]() and 1 are the solutions of equation mx2 + nx + 6 = 0. Find the values of m and n.
and 1 are the solutions of equation mx2 + nx + 6 = 0. Find the values of m and n.
For x = ![]() and x = 1 to be solutions of the given quadratic equation it should satisfy the equation
and x = 1 to be solutions of the given quadratic equation it should satisfy the equation
So, substituting x = ![]() and x = 1 in the given equation, we get
and x = 1 in the given equation, we get
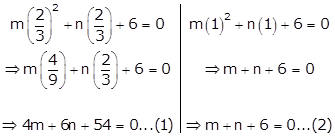
Solving equations (1) and (2) simultaneously,
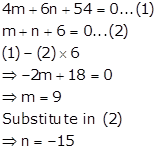
If 3 and -3 are the solutions of equation ax2 + bx - 9 = 0. Find the values of a and b.
For x = 3 and x = -3 to be solutions of the given quadratic equation it should satisfy the equation
So, substituting x = 3 and x = -3 in the given equation, we get
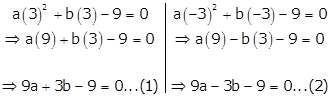
Solving equations (1) and (2) simultaneously,


No comments:
Post a Comment