Solve : ![]()
![]()

Solve : ![]()
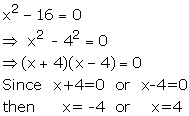
Solve : ![]()
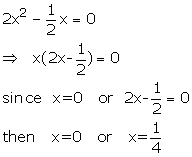
Solve : ![]()
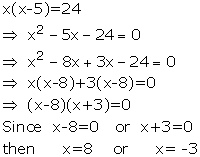
Solve : ![]()

Solve : ![]()
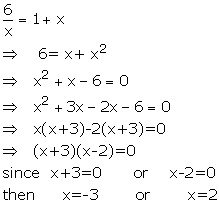
Solve : ![]()

Solve : ![]()
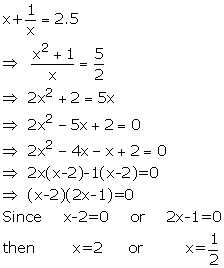
Solve : ![]()
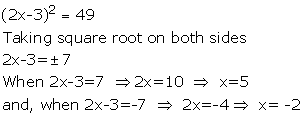
Solve : ![]()

Solve : ![]()

Solve : ![]()
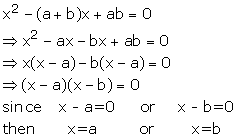
Solve : ![]()
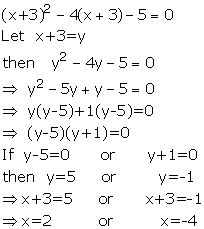
Solve : ![]()
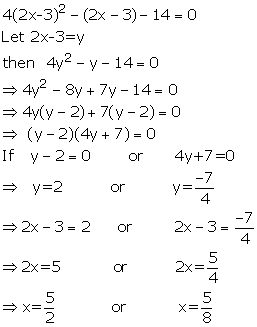
Solve : ![]()
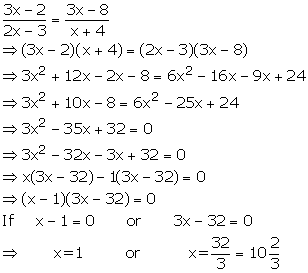
2x2 - 9x + 10 = 0, When
(i) x∈ N
(ii) x∈ Q
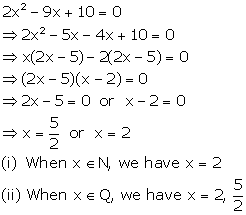
Solve : ![]()
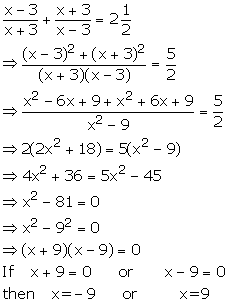
Solve : ![]()
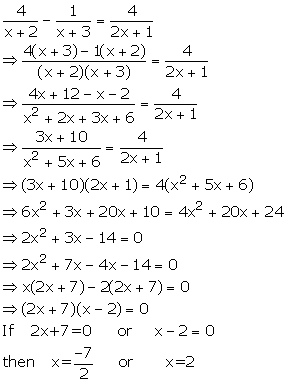
Solve : ![]()
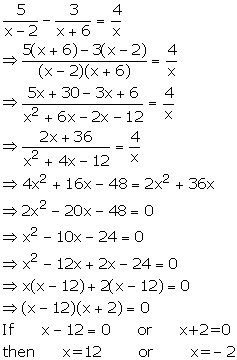
Solve : ![]()

Find the quadratic equation, whose solution set is :
(i)![]() (ii)
(ii)![]()


![]()
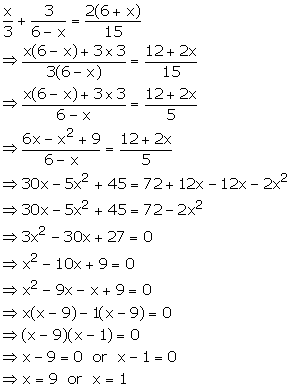
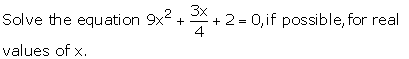
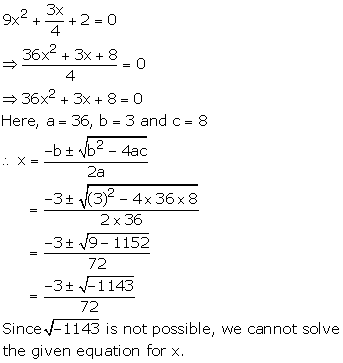
Find the value of x, if a + 1=0 and x2 + ax - 6 =0.
If a+1=0, then a = -1
Put this value in the given equation x2 + ax - 6 =0
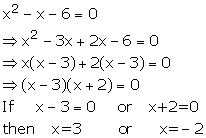
Find the value of x, if a + 7=0; b + 10=0 and 12x2 = ax - b.
If a + 7 =0, then a = -7
and b + 10 =0, then b = - 10
Put these values of a and b in the given equation
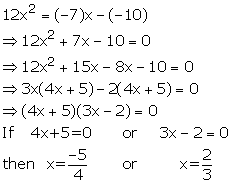
Use the substitution y= 2x +3 to solve for x, if 4(2x+3)2 - (2x+3) - 14 =0.
4(2x+3)2 - (2x+3) - 14 =0
Put 2x+3 = y
Question 26
Without solving the quadratic equation 6x2 - x - 2=0, find whether ![]() is a solution of this equation or not.
is a solution of this equation or not.
Consider the equation, 6x2 - x - 2=0
Put ![]() in L.H.S.
in L.H.S.
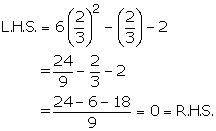
Since L.H.S.= R.H.S., then ![]() is a solution of the given equation.
is a solution of the given equation.
x2 - 3x +2=0
Put x = -1 in L.H.S.
L.H.S. = (-1)2 - 3(-1) +2
= 1 +3 +2=6 ![]() R.H.S.
R.H.S.
Then x = -1 is not the solution of the given equation.
Find the value of m.
Given x = ![]() is the solution of the given equation.
is the solution of the given equation.
Put given value of x in the given equation
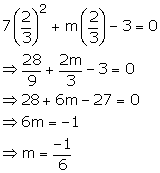
If x = -3 and x = ![]() are solutions of quadratic equation mx2 + 7x + n = 0, find the values of m and n.
are solutions of quadratic equation mx2 + 7x + n = 0, find the values of m and n.
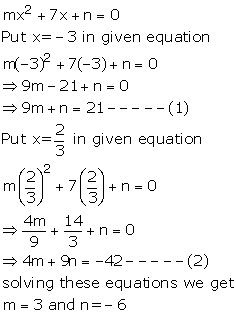
If quadratic equation x2 - (m + 1) x + 6=0 has one root as x =3;
find the value of m and the root of the equation.
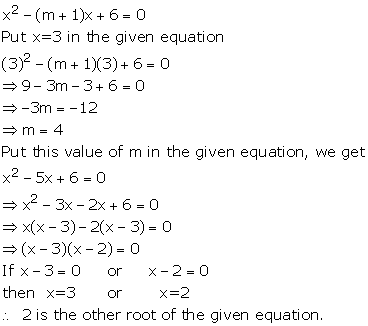
Given that 2 is a root of the equation 3x2 - p(x + 1) = 0 and that the equation px2 - qx + 9 = 0 has equal roots, find the values of p and q.
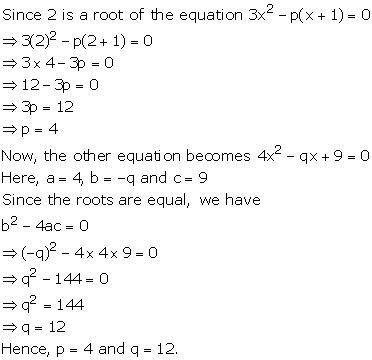
![]()
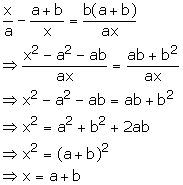
or x = -(a + b)
![]()
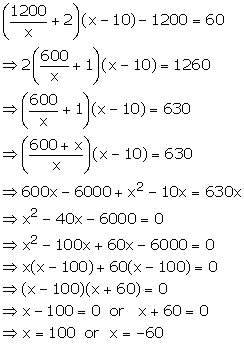
If -1 and 3 are the roots of x2+px+q=0
then find the values of p and q

No comments:
Post a Comment