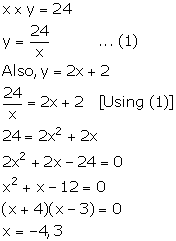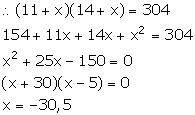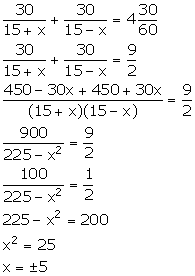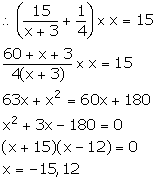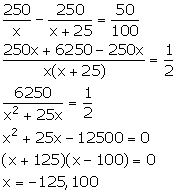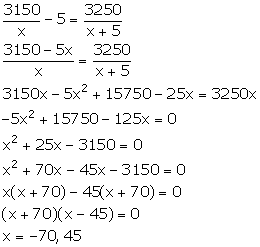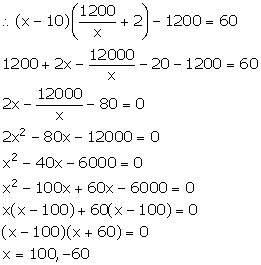Chapter 6 - Solving (simple) Problems (Based on Quadratic Equations) Exercise Ex. 6(E)

Question 1

The distance by road between two towns A and B is 216 km, and by rail it is 208 km. A car travels at a speed of x km/hr and the train travels at a speed which is 16 km/hr faster than the car. Calculate:

(i) the time taken by the car to reach town B from A, in terms of x;

(ii) the time taken by the train to reach town B from A, in terms of x.

(iii) If the train takes 2 hours less than the car, to reach town B, obtain an equation in x and solve it.

(iv) Hence, find the speed of the train

Solution 1

Question 2

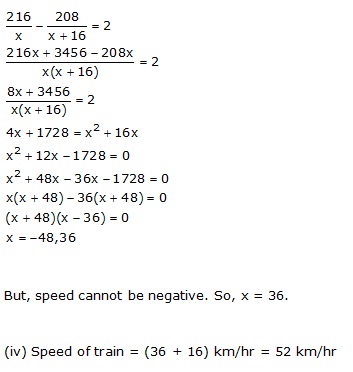
A trader buys x articles for a total cost of Rs 600.

(i) Write down the cost of one article in terms of x.

If the cost per article were Rs 5 more, the number of articles that can be bought for Rs 600 would be four less.

(ii) Write down the equation in x for the above situation and solve it for x.

Solution 2

Question 3

A hotel bill for a number of people for overnight stay is Rs 4800. If there were 4 people more, the bill each person had to pay, would have reduced by Rs 200. Find the number of people staying overnight.

Solution 3

Question 4

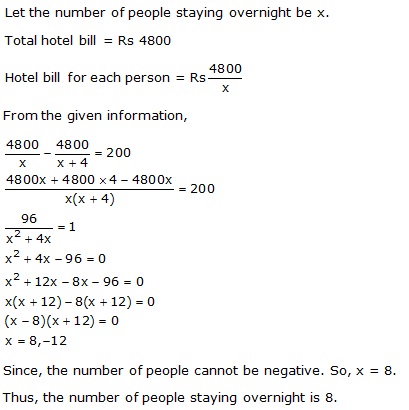
An Aero plane travelled a distance of 400 km at an average speed of x km/hr. On the return journey, the speed was increased by 40 km/hr. Write down an expression for the time taken for:

(i) the onward journey;

(ii) the return journey.

If the return journey took 30 minutes less than the onward journey, write down an equation in x and find its value.

Solution 4

Question 5

Rs 6500 was divided equally among a certain number of persons. Had there been 15 persons more, each would have got Rs 30 less. Find the original number of persons.

Solution 5

Question 6

A plane left 30 minutes later than the schedule time and in order to reach its destination 1500 km away in time, it has to increase its speed by 250 km/hr from its usual speed. Find its usual speed.

Solution 6

Question 7

Two trains leave a railway station at the same time. The first train travels due west and the second train due north. The first train travels 5 km/hr faster than the second train. If after 2 hours, they are 50 km apart, find the speed of each train.

Solution 7

Question 8

The sum S of first n even natural numbers is given by the relation S = n(n + 1). Find n, if the sum is 420.

Solution 8

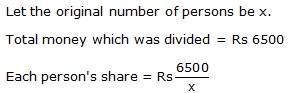
S = n(n + 1)

Given, S = 420

n(n + 1) = 420

n² + n - 420 = 0

n² + 21n - 20n - 420 = 0

n(n + 21) - 20(n + 21) = 0

(n + 21) (n - 20) = 0

n = -21, 20

Since, n cannot be negative.

Hence, n = 20.

Question 9

The sum of the ages of a father and his son is 45 years. Five years ago, the product of their ages (in years) was 124. Determine their present ages.

Solution 9

Let the present ages of father and his son be x years and (45 - x) years respectively.

 Five years ago,

Father's age = (x - 5) years

Son's age = (45 - x - 5) years = (40 - x) years

 From the given information, we have:

(x - 5) (40 - x) = 124

40x - x² - 200 + 5x = 124

x² - 45x +324 = 0

x² - 36x - 9x +324 = 0

x(x - 36) - 9(x - 36) = 0

(x - 36) (x - 9) = 0

x = 36, 9

 If x = 9,

Father's age = 9 years, Son's age = (45 - x) = 36 years

This is not possible.

Hence, x = 36

Father's age = 36 years

Son's age = (45 - 36) years = 9 years

Question 10

In an auditorium, seats were arranged in rows and columns. The number of rows was equal to the number of seats in each row. When the number of rows was doubled and the number of seats in each row was reduced by 10, the total number of seats increased by 300. Find:

(i) the number of rows in the original arrangement.

(ii) the number of seats in the auditorium after re-arrangement.

Solution 10

Let the number of rows in the original arrangement be x.

Then, the number of seats in each row in original arrangement = x

Total number of seats =

 From the given information,

2x(x - 10) = x² + 300

2x² - 20x = x² + 300

x² - 20x - 300 = 0

(x - 30) (x + 10) = 0

x = 30, -10

 Since, the number of rows or seats cannot be negative. So, x = 30.

 (i) The number of rows in the original arrangement = x = 30

(ii) The number of seats after re-arrangement = x² + 300 = 900 + 300 = 1200

Question 11

Mohan takes 16 days less than Manoj to do a piece of work. If both working together can do it in 15 days, in how many days will Mohan alone complete the work?

Solution 11

Question 12

Two years ago, a man's age was three times the square of his son's age. In three years time, his age will be four times his son's age. Find their present ages.

Solution 12

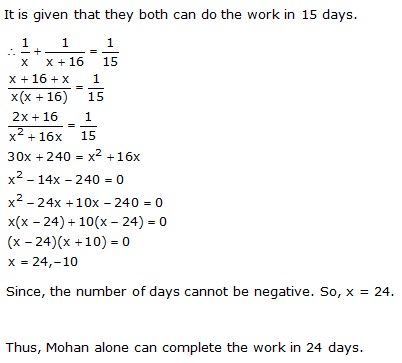
Let the age of son 2 years ago be x years.

Then, father's age 2 years ago = 3x² years

 

Present age of son = (x + 2) years

Present age of father = (3x² + 2) years

 

3 years hence:

Son's age = (x + 2 + 3) years = (x + 5) years

Father's age = (3x² + 2 + 3) years = (3x² + 5) years

 

From the given information,

3x² + 5 = 4(x + 5)

3x² - 4x - 15 = 0

3x² - 9x + 5x - 15 = 0

3x(x - 3) + 5(x - 3) = 0

(x - 3) (3x + 5) = 0

x = 3,

Since, age cannot be negative. So, x = 3.

 

Present age of son = (x + 2) years = 5 years

Present age of father = (3x² + 2) years = 29 years

Question 13

In a certain positive fraction, the denominator is greater than the numerator by 3. If 1 is subtracted from the numerator and the denominator both, the fraction reduces by 1/14. Find the fraction.

Solution 13

Question 14

In a two digit number, the ten's digit is bigger. The product of the digits is 27 and the difference between two digits is 6. Find the number.

Solution 14

Given, the difference between two digits is 6 and the ten's digit is bigger than the unit's digit.

So, let the unit's digit be x and ten's digit be (x + 6).

 

From the given condition, we have:

x(x + 6) = 27

x² + 6x - 27 = 0

x² + 9x - 3x - 27 = 0

x(x + 9) - 3(x + 9) = 0

(x + 9) (x - 3) = 0

x = -9, 3

 

Since, the digits of a number cannot be negative. So, x = 3.

 

Unit's digit = 3

Ten's digit = 9

 

Thus, the number is 93.

Question 15

Some school children went on an excursion by a bus to a picnic spot at a distance of 300 km. While returning, it was raining and the bus had to reduce its speed by 5 km/hr and it took two hours longer for returning. Find the time taken to return.

Solution 15

Question 16

Rs.480 is divided equally among 'x' children. If the number of children were 20 more, then each would have got Rs.12 less. Find 'x'.

Solution 16

Question 17

A bus covers a distance of 240 km at a uniform speed. Due to heavy rain its speed gets reduced by 10km/h and as such it takes two hrs longer to cover the total distance. Assuming the uniform speed to be 'x' km/h, form an equation and solve it to evaluate 'x'.

Solution 17

Time taken by bus to cover total distance with speed x km/h =  

Time taken by bus to cover total distance with speed (x - 10) km/h =  

According to the given condition, we have 

 

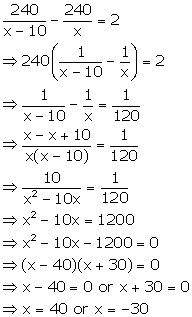
Since the speed cannot be negative, we have x = 40 km/h

Question 18

The sum of the ages of Vivek and his younger brother Amit is 47 years. The product of their ages in years is 550. Find their ages.

Solution 18

Given that he sum of the ages of Vivek and his younger brother Amit is 47 years.

Let the age of Vivek = x

⇒ the age of Amit = 47 - x 

The product of their ages in years is 550 …. given

⇒ x(47 - x) = 550

⇒ 47x - x² = 550

⇒ x² - 47x + 550 = 0  

⇒ x² - 25x - 22x  + 550 = 0

⇒ x(x - 25) - 22(x - 25) = 0

⇒ (x - 25) (x - 22) = 0

⇒ x = 25 or x = 22

Given that Vivek is an elder brother.

∴ x = 25 years = age of Vivek and

age of Amit = 47 - 25 = 22 years  

Chapter 6 - Solving (simple) Problems (Based on Quadratic Equations) Exercise Ex. 6(D)

Question 1

The sum S of n successive odd numbers starting from 3 is given by the relation: S = n(n + 2). Determine n, if the sum is 168

Solution 1

From the given information, we have:

n(n + 2) = 168

n² + 2n - 168 = 0

n² + 14n - 12n - 168 = 0

n(n + 14) - 12(n + 14) = 0

(n + 14) (n - 12) = 0

n = -14, 12

But, n cannot be negative.

Therefore, n = 12.

Question 2

A stone is thrown vertically downwards and the formula d = 16t² + 4t gives the distance, d metres, that it falls in t seconds. How long does it take to fall 420 metres?

Solution 2

From the given information,

16t² + 4t = 420

4t² + t - 105 = 0

4t² - 20t + 21t - 105 = 0

4t(t - 5) + 21(t - 5) = 0

(4t + 21)(t - 5) = 0

t = , 5

But, time cannot be negative.

Thus, the required time taken is 5 seconds.

Question 3

The product of the digits of a two digit number is 24. If its unit's digit exceeds twice its ten's digit by 2; find the number.

Solution 3

Let the ten's and unit's digit of the required number be x and y respectively.

From the given information,

The digit of a number cannot be negative, so, x = 3.

Thus, the required number is 38.

Question 4

The ages of two sisters are 11 years and 14 years. In how many years time will the product of their ages be 304?

Solution 4

The ages of two sisters are 11 years and 14 years.

Let in x number of years the product of their ages be 304.

But, the number of years cannot be negative. So, x = 5.

Hence, the required number of years is 5 years.

Question 5

One year ago, a man was 8 times as old as his son. Now his age is equal to the square of his son's age. Find their present ages.

Solution 5

Let the present age of the son be x years.

Present age of man = x² years

One year ago,

Son's age = (x - 1) years

Man's age = (x² - 1) years

It is given that one year ago; a man was 8 times as old as his son.

 (x² - 1) = 8(x - 1)

x² - 8x - 1 + 8 = 0

x² - 8x + 7 = 0

(x - 7) (x - 1) = 0

x = 7, 1

If x = 1, then x² = 1, which is not possible as father's age cannot be equal to son's age.

So, x = 7.

Present age of son = x years = 7 years

Present age of man = x² years = 49 years.

Question 6

The age of the father is twice the square of the age of his son. Eight years hence, the age of the father will be 4 years more than three times the age of the son. Find their present ages.

Solution 6

Let the present age of the son be x years.

 Present age of father = 2x² years

Eight years hence,

Son's age = (x + 8) years

Father's age = (2x² + 8) years

It is given that eight years hence, the age of the father will be 4 years more than three times the age of the son.

 2x² + 8 = 3(x + 8) +4

2x² + 8 = 3x + 24 +4

2x² - 3x - 20 = 0

2x² - 8x + 5x - 20 = 0

2x(x - 4) + 5(x - 4) = 0

(x - 4) (2x + 5) = 0

x = 4, 

But, the age cannot be negative, so, x = 4.

 Present age of son = 4 years

Present age of father = 2(4)² years = 32 years

Question 7

The speed of a boat in still water is 15 km/hr. It can go 30 km upstream and return downstream to the original point in 4 hours 30 minutes. Find the speed of the stream.

Solution 7

Let the speed of the stream be x km/hr.

 Speed of the boat downstream = (15 + x) km/hr

Speed of the boat upstream = (15 - x) km/hr

Time taken to go 30 km downstream = 

Time taken to come back = 

From the given information,

But, x cannot be negative, so, x = 5.

Thus, the speed of the stream is 5 km/hr.

Question 8

Mr. Mehra sends his servant to the market to buy oranges worth Rs 15. The servant having eaten three oranges on the way. Mr. Mehra pays Rs 25 paise per orange more than the market price.

Taking x to be the number of oranges which Mr. Mehra receives, form a quadratic equation in x. Hence, find the value of x.

Solution 8

Number of oranges = y

Cost of one orange = 

The servant ate 3 oranges, so Mr. Mehra received (y - 3) oranges.

So, x = y - 3  y = x + 3 ...(1)

Cost of one orange paid by Mr. Mehra = 

                                                         =

Now, Mr. Mehra pays a total of Rs 15.

But, the number of oranges cannot be negative. So, x = 12.

Question 9

Rs 250 is divided equally among a certain number of children. If there were 25 children more, each would have received 50 paise less. Find the number of children.

Solution 9

Let the number of children be x.

It is given that Rs 250 is divided amongst x students.

So, money received by each child = Rs

If there were 25 children more, then

Money received by each child = Rs

From the given information,

Since, the number of students cannot be negative, so, x = 100.

Hence, the number of students is 100.

Question 10

An employer finds that if he increased the weekly wages of each worker by Rs 5 and employs five workers less, he increases his weekly wage bill from Rs 3,150 to Rs 3,250. Taking the original weekly wage of each worker as Rs x; obtain an equation in x and then solve it to find the weekly wages of each worker.

Solution 10

Original weekly wage of each worker = Rs x

Original weekly wage bill of employer = Rs 3150

Number of workers = 

New weekly wage of each worker = Rs (x + 5)

New weekly wage bill of employer = Rs 3250

Number of workers = 

From the given condition,

Since, wage cannot be negative, x = 45.

Thus, the original weekly wage of each worker is Rs 45.

Question 11

A trader bought a number of articles for Rs 1,200. Ten were damaged and he sold each of the remaining articles at Rs 2 more than what he paid for it, thus getting a profit of Rs 60 on whole transaction.

Taking the number of articles he bought as x, form an equation in x and solve it.

Solution 11

Number of articles bought by the trader = x

It is given that the trader bought the articles for Rs 1200.

So, cost of one article = Rs

Ten articles were damaged. So, number of articles left = x - 10

Selling price of each of (x - 10) articles = Rs

Selling price of (x - 10) articles = Rs (x - 10) 

Profit = Rs 60

Number of articles cannot be negative. So, x = 100.

Question 12

The total cost price of a certain number of identical articles is Rs 4800. By selling the articles at Rs 100 each, a profit equal to the cost price of 15 articles is made. Find the number of articles bought.

Solution 12

Let the number of articles bought be x.

Total cost price of x articles = Rs 4800

Cost price of one article = Rs

Selling price of each article = Rs 100

Selling price of x articles = Rs 100x

Given, Profit = C.P. of 15 articles

 100x - 4800 = 15 

100x² - 4800x = 15  4800

x² - 48x - 720 = 0

x² - 60x + 12x - 720 = 0

x(x - 60) + 12(x - 60) = 0

(x - 60) (x + 12) = 0

x = 60, -12

Since, number of articles cannot be negative. So, x = 60.

Thus, the number of articles bought is 60.